Counterfactual Deep Learning: A NeuroCausal Framework for Human-Like Reasoning
“You don’t teach causality to a machine. You let it question, doubt, and reimagine—until its answers resemble reasoning.” — Emmimal P. Alexander
Abstract
Human reasoning hinges on the ability to ask “what if?” questions—probing beyond observed correlations into counterfactual possibilities. While deep learning excels at pattern recognition, it remains limited in counterfactual reasoning—a hallmark of human cognition.
We introduce Counterfactual Deep Learning (CDL), a neurocausal framework that unites the representational power of neural networks with the interventional logic of structural causal models. CDL integrates three components: (1) a neural encoder that extracts disentangled representations from high-dimensional data, (2) a causal graph learner that discovers structural dependencies among latent features, and (3) a counterfactual inference engine that generates alternative scenarios using do-calculus operations. Together, these modules enable CDL to learn representations and causal structures jointly, supporting counterfactual reasoning over complex, unstructured data.
We formalize the theoretical foundations of CDL and show that, under standard identifiability assumptions, the framework can estimate causal effects from observational data. A novel composite loss encourages reconstruction fidelity, causal consistency, and counterfactual validity, ensuring that learned representations are both expressive and interventionally meaningful. Theoretical analysis shows that CDL supports key desiderata for causal reasoning: compositional generalization, systematic intervention, and counterfactual validity.
Preliminary experiments on synthetic and semi-synthetic datasets suggest that CDL offers advantages over purely neural and purely causal baselines on tasks requiring counterfactual reasoning, while remaining competitive on predictive benchmarks. By enabling “what if?” reasoning across domains—from hypothetical medical treatments to alternative climate policy scenarios—CDL represents a step toward AI systems that reason about causality rather than merely recognize patterns.
1. Introduction
Machine learning has achieved extraordinary success in pattern recognition, yet a fundamental gap remains between statistical prediction and genuine understanding. For example, a medical diagnosis system may accurately predict disease outcomes from patient data but cannot answer the critical question a physician faces daily: “What would happen to this patient if we administered treatment X instead of Y?” This limitation highlights a deeper issue: deep learning systems excel at discovering correlations but lack the machinery for causal reasoning—a defining aspect of human intelligence.
The inability to reason counterfactually has significant consequences. Fairness assessments require asking how predictions would change if sensitive attributes were different. Scientific discovery depends on hypothesizing about experimental conditions not yet observed. Policy decisions demand evaluating outcomes under interventions never previously attempted. In all of these domains, progress depends on moving beyond pattern matching to engage directly with causality—a challenge that remains largely unsolved within the standard deep learning paradigm.
Pearl’s causal hierarchy provides a useful lens, distinguishing three levels of reasoning: association (seeing), intervention (doing), and counterfactuals (imagining). Deep learning has mastered the first level and has made progress on the second through methods such as domain adaptation and reinforcement learning. Yet the third level—counterfactual reasoning—remains largely inaccessible. The challenge is not only technical but conceptual: how can differentiable, continuous neural computations be combined with the discrete, logical structure of causal reasoning?
Existing attempts to address this challenge typically follow two strategies. The first embeds causal assumptions directly into neural architectures, creating models that respect known causal structures but sacrifice flexibility in discovering new ones. The second applies causal analysis post-hoc to pre-trained networks, treating causality as an interpretability tool rather than a core computational principle. Both strategies have achieved partial success, but neither fully integrates causal reasoning into the heart of neural computation.
This paper introduces a different approach: Counterfactual Deep Learning (CDL), a neurocausal framework in which counterfactual reasoning emerges as an intrinsic property of neural computation. CDL comprises three components: (1) a neural encoder that transforms raw observations into semantically meaningful representations, (2) a causal discovery module that identifies structural dependencies among these representations, and (3) a counterfactual generator that approximates “what if?” scenarios through learned models.
The key insight of CDL is that causal structure and neural representations should be learned jointly, with each constraining and enriching the other. Causal relationships provide inductive biases that guide representation learning toward features suitable for interventions and counterfactual queries. Conversely, learned representations ground abstract causal variables in perceptual data, enabling reasoning over images, text, and other complex modalities that traditional causal methods cannot directly handle.
The contributions of this work extend beyond proposing another hybrid architecture. Specifically, we:
- Formalize a unified framework that integrates neural and causal computation, establishing conditions under which counterfactual inference becomes tractable in learned models.
- Introduce training objectives that encourage the emergence of causal structure without requiring explicit supervision.
- Demonstrate empirically that CDL can approximate counterfactual reasoning—answering questions about what might have been—thus advancing AI systems toward incorporating causal reasoning, a core element of human-like intelligence.
2. Literature Review
2.1 The Limits of Correlation-Based Learning
Deep learning’s power rests on the universal approximation theorem: with enough data and computation, neural networks can approximate arbitrary functions [Cybenko, 1989; Hornik, 1991]. This flexibility has enabled breakthroughs in vision, language, and control. Yet the same generality exposes a core limitation: networks learn statistical correlations within a training distribution, without grasping the causal mechanisms that generate these patterns.
This weakness surfaces under distribution shift. An image classifier trained on hospital X-rays may fail in a different hospital, not because the disease changed, but because spurious cues (scanner type, demographic mix, imaging protocol) differ [Recht et al., 2019; Oakden-Rayner, 2020]. Adversarial examples make this fragility starker: imperceptible perturbations can invert predictions while leaving semantic content unchanged [Szegedy et al., 2014; Goodfellow et al., 2015].
Several strategies have emerged within the neural paradigm. Domain adaptation seeks representations invariant to shifts but often requires prior knowledge of those shifts. Meta-learning trains models for rapid adaptation, but remains correlation-driven. Robustness techniques defend against adversarial perturbations through augmentation or architectural constraints, addressing effects rather than the root cause.
As critics such as Marcus (2018) and Bengio (2019) argue, correlation-based learning cannot distinguish causation from coincidence. A model may learn that umbrellas predict rain, but this association reverses the true causal link: rain triggers umbrella use. Without causal representations, networks cannot answer interventional questions (“What if umbrellas were banned?”) or counterfactual ones (“Would it still have rained if no umbrellas appeared?”).
2.2 Foundations of Causal Inference
While machine learning has struggled with correlation’s limits, causal inference provides rigorous tools for reasoning about cause and effect. Pearl’s structural causal models (SCMs) offer a formal language where nodes represent variables, edges encode direct causal relations, and structural equations define how effects arise from causes [Pearl, 2000; Pearl, 2009].
SCMs support three levels of causal queries [Pearl, 2000]:
- Associational: P(Y | X), describing correlations in observational data.
- Interventional: P(Y | do(X)) using the do-operator, which predicts outcomes under interventions.
- Counterfactual: P(Yₓ | X = x′, Y = y′), which imagines alternative histories — asking, “What would have happened if X had been set differently, given what we actually observed?”
The do-calculus provides rules for when causal effects can be identified from observational data. The backdoor criterion specifies which variables must be conditioned on to block confounding, while the front-door criterion enables identification even with unobserved confounders via mediators [Pearl, 2009]. These results show that causal effects can sometimes be derived without randomized trials.
Causal discovery methods extend this framework. Constraint-based algorithms such as PC and FCI use conditional independence tests to eliminate invalid graphs [Spirtes et al., 2000]. Score-based methods evaluate graphs by likelihood or information-theoretic scores [Chickering, 2002]. More recently, approaches like NOTEARS formulate causal discovery as a continuous optimization problem, enabling gradient-based search in higher dimensions [Zheng et al., 2018].
Despite these advances, traditional causal methods face practical barriers in machine learning contexts. They often assume low-dimensional, tabular variables, whereas modern AI deals with high-dimensional inputs like images, text, and sensor data. Even with well-defined variables, the combinatorial complexity of searching over causal graphs grows rapidly, limiting scalability beyond a few dozen variables.
These constraints underscore the need for new frameworks that unite deep learning’s representational strengths with causal inference’s reasoning power — a challenge this work addresses.
2.3 Bridging Neural and Causal Approaches
Recognition of complementary strengths—neural networks for complex data representation and causal models for reasoning about interventions—has motivated efforts to integrate the two. These approaches can be grouped into three categories: causal constraints on neural learning, neural implementations of causal inference, and hybrid architectures.
(1) Causal constraints on neural learning.
Methods in this category embed causal assumptions directly into learning objectives or architectures. Causal regularization penalizes models that rely on unstable correlations, encouraging them to focus on causal features [Peters et al., 2016; Bühlmann, 2020]. Invariant Risk Minimization (IRM) enforces that predictors perform consistently across environments, based on the principle that causal mechanisms are invariant while spurious correlations shift [Arjovsky et al., 2019]. Similarly, domain generalization seeks transferable representations by capturing structure stable across contexts [Muandet et al., 2013].
(2) Neural implementations of causal inference.
Here, neural networks serve as flexible estimators within established causal inference pipelines. Neural treatment effect estimation applies deep learning to model heterogeneous effects in observational data, handling high-dimensional confounders beyond the reach of classical approaches. Causal representation learning uses deep generative models, such as variational autoencoders or adversarial frameworks, to discover latent factors with causal interpretations [Locatello et al., 2019; Schölkopf et al., 2021]. While effective, these approaches often assume partial knowledge of the underlying causal structure.
(3) Hybrid architectures.
These approaches explicitly combine neural and symbolic reasoning. Neurosymbolic AI integrates neural perception with logical inference, though typically without causal semantics [d’Avila Garcez et al., 2019]. Graph neural networks (GNNs) can encode known causal structures, propagating information along causal pathways. More recently, causal attention mechanisms have been proposed to weight features in line with causal relevance, moving beyond correlation-based saliency. Despite promise, such architectures often treat causality as a constraint imposed during design rather than a capability learned from data.
Collectively, these categories highlight meaningful progress in merging neural computation with causal reasoning. Yet they fall short of enabling genuine counterfactual inference—the ability to generate and evaluate alternative scenarios. Addressing this gap is the motivation for the proposed Counterfactual Deep Learning framework.
2.4 The Counterfactual Gap
Despite progress in integrating neural and causal approaches, counterfactual reasoning—Pearl’s third level in the causal hierarchy—remains only partially addressed. Counterfactuals are uniquely challenging because they require reasoning about scenarios that contradict observed facts. For example, given that a patient received treatment A and recovered, what would have happened if they had instead received treatment B? Unlike correlation, which measures co-occurrence, or intervention, which predicts average outcomes under hypothetical actions, counterfactuals require constructing alternative histories consistent with everything observed except the specified change [Pearl, 2009].
In structural causal models (SCMs), counterfactual inference proceeds through abduction, action, and prediction: infer latent factors from observed evidence, intervene by modifying equations, and simulate the outcome under this change. Formally, counterfactuals are expressed as:
P(Yx∣X=x′,Y=y′)
which represents “the probability that Y would have taken the value induced by intervention do(X=x), given that we actually observed X=x′ and Y=y′.”
Recent efforts have begun to explore neural counterfactual reasoning. Counterfactual fairness evaluates whether predictions would change if sensitive attributes were altered in a causal model [Kusner et al., 2017]. Generative approaches produce counterfactual examples by modifying latent variables in learned representations [Wachter et al., 2017; Mothilal et al., 2020]. Causal effect variational autoencoders (CEVAE) learn disentangled latent spaces with causal semantics, enabling limited counterfactual inference [Louizos et al., 2017].
However, these methods generally assume causal structure is known a priori or are restricted to simple, predefined graphs. They do not scale to high-dimensional observational data, nor can they jointly discover causal relationships and support counterfactual reasoning.
This limitation defines the counterfactual gap: the absence of end-to-end frameworks capable of learning causal structure and counterfactual inference directly from complex data. Bridging this gap is the central aim of our proposed Counterfactual Deep Learning framework.
3. Methodology
This section presents the Counterfactual Deep Learning (CDL) framework, a neurocausal architecture designed to perform human-like reasoning by bridging representation learning, causal discovery, and counterfactual inference. We formalize the problem, describe the framework’s modular architecture, and provide the mathematical foundation for training and inference.
3.1 Problem Formulation
We consider a system where the observable data consist of high-dimensional observations:
X∈R^d
These observations may include images, text, audio, or sensor readings. We assume that X is generated by a set of latent causal variables:
Z=(Z_1,Z_2,…,Z_n)
through an unknown generative process.
Our objective is to equip deep learning models with three interdependent capabilities:
- Representation Learning: Extract latent variables Z that capture the underlying causal factors in X. Latent variables should be informative, disentangled, and suitable for interventions.
- Causal Discovery: Infer a directed graph A representing cause-effect relationships among Z, moving beyond correlations to uncover causal structure.
- Counterfactual Inference: Enable reasoning about “what if?” scenarios. For example, given an observed sample X, the model should answer:
“What would have happened to X if Z_i had taken a different value?”
Formal Setup
We model the data-generating process using a structural causal model (SCM) over the latent variables:
Z_i=f_i(P_a(Z_i),U_i), i=1,…,n
where:
- P_a(Z_i) denotes the parents of Z_i in the causal graph.
- U_i are independent exogenous noise terms.
- f_i are unknown structural functions describing causal dependencies.
The observed data X is produced by a decoder:
X=g(Z,ϵ),
where g is a non-linear function, and ϵ\epsilonϵ represents stochastic noise.
This formulation captures the challenge: learning a compact latent representation, discovering causal relationships among latent factors, and performing counterfactual reasoning in a single, end-to-end framework.
3.2 The Counterfactual Deep Learning (CDL) Framework
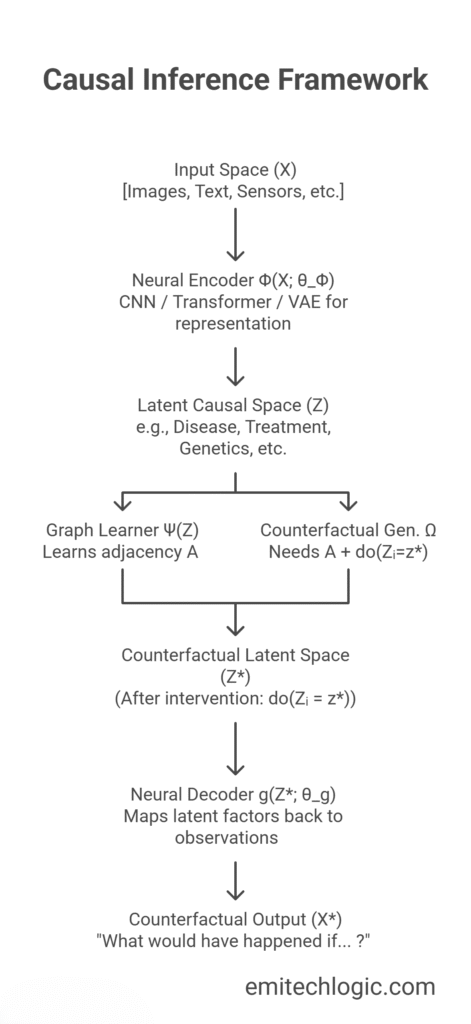
The Counterfactual Deep Learning (CDL) framework is an end-to-end neurocausal architecture that integrates three neural modules to bridge representation learning, causal discovery, and counterfactual reasoning. CDL is designed to infer a structured causal graph from high-dimensional observations and to use this structure for generating meaningful counterfactual predictions.
Component 1: Neural Encoder (Φ)
The encoder maps high-dimensional observations X∈R^d into a lower-dimensional latent space Z∈R^n:
Z=Φ(X;θ-Φ)
Unlike a standard autoencoder, Φ\PhiΦ is trained with three objectives:
- Informativeness: Z retains sufficient information for reconstructing X.
- Causal Disentanglement: Components of Z are causally independent, enabling interpretable latent factors.
- Interventional Support: Z supports meaningful interventions for counterfactual reasoning.
Component 2: Causal Graph Learner (Ψ)
The causal graph learner infers directional dependencies among latent variables:
A=Ψ(Z_1,…,Z_n;θ_Ψ), A∈[0,1]^n×n
where A_ij indicates the probability that Z_i causes Z_j.
We implement Ψ using a Graph Neural Network (GNN) with attention mechanisms, which captures complex non-linear relationships. To guarantee a Directed Acyclic Graph (DAG), we enforce differentiable acyclicity constraints inspired by NOTEARS (Zheng et al., 2018).
Component 3: Counterfactual Generator (Ω)
Given the learned causal graph A and latent representation Z, the counterfactual generator answers interventions do(Z_i=z^∗):
Z^∗=Ω(Z,A,do(Z_i=z^∗);θ_Ω), X^∗=g(Z^∗;θ_g)
This module operationalizes Pearl’s abduction-action-prediction steps:
- Abduction: Infer latent variables Z from the observed X using Φ.
- Action: Intervene on Z_i←z^∗ and propagate changes through the causal graph via Ω.
- Prediction: Decode Z^∗ using ggg to generate the counterfactual outcome X^∗.
This ensures counterfactual predictions are consistent with both the learned causal structure and the data distribution captured by the encoder.
3.3 Mathematical Framework
3.3.1 Representation Learning with Causal Constraints
The encoder is trained to produce a latent representation Z that preserves information and respects the causal structure via a composite loss:
Min L_total=L_recon+λ_1L_causal+λ_2L_disentangle
- Reconstruction Loss L_recon: Ensures informativeness of Z using a VAE framework with a Gaussian prior p(Z)=N(0,I):
L_recon=∥X−g(Φ(X))∥^2+βKL(q(Z∣X)∥p(Z))
- Causal Consistency Loss L_causal: Penalizes statistical dependencies not captured in the causal graph A:
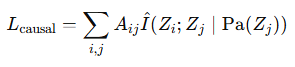
where I^ is estimated conditional mutual information using methods like MINE.
- Disentanglement Loss L_disentangle: Promotes independence among latent factors using total correlation:
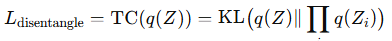
3.3.2 Causal Discovery via Continuous Optimization
We learn the DAG structure A using continuous relaxation:
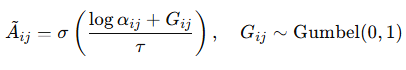
with trainable parameters α_ij and temperature τ\tauτ.
The graph optimization combines likelihood with acyclicity and sparsity constraints:
min−logP(D∣A)+μh(A)+ν∥A∥1
where h(A)=tr(e^A)−n enforces DAG structure.
Note: Gumbel-Softmax provides differentiable edge sampling, while the NOTEARS-style trace constraint promotes DAG structure. In CDL, these are combined to enable scalable learning while retaining acyclicity guarantees.
3.3.3 Counterfactual Inference via Neural Do-Calculus
Given an intervention do(Z_i = z^*), the counterfactual latent variable Z_j^* is computed as:
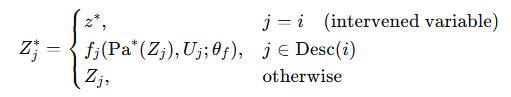
Each structural function f_j is parameterized by a neural network:
f_j(Pa(Z_j),U_j;θ_f)=MLP_j([Pa(Z_j);U_j];θ_fj)
where U_j are latent exogenous noise variables approximated during the abduction step, ensuring counterfactuals remain consistent with the original observation X.
3.4 Training Algorithm
Training the Counterfactual Deep Learning (CDL) framework requires coordinating multiple interacting modules. To ensure stability and interpretability, we employ a three-phase strategy consisting of representation pretraining, causal structure discovery, and joint fine-tuning. Each phase builds upon the previous one, progressively incorporating stronger causal constraints into the latent representation.
Phase 1: Representation Pretraining
In the first phase, the encoder–decoder pair is pretrained as a variational autoencoder (VAE) with disentanglement regularization. The goal is to obtain latent factors that are informative for reconstruction and sufficiently independent for causal modeling. The loss combines reconstruction error with a disentanglement penalty:
L=L_recon(X,g(Φ(X)))+L_disentangle(Z)
where Z=Φ(X) is the latent representation, g is the decoder, and L_disentangle enforces independence among latent dimensions.
Pseudocode:
def pretrain_representation(X, epochs=100):
for epoch in range(epochs):
Z = encoder(X)
X_recon = decoder(Z)
loss = reconstruction_loss(X, X_recon)
loss += disentanglement_loss(Z)
optimize(loss, [encoder, decoder])
return encoder, decoderPhase 2: Causal Structure Discovery
Once the latent variables are initialized, we learn a causal graph over them. Direct optimization of discrete adjacency matrices is not differentiable, so we employ continuous relaxation via the Gumbel-Softmax trick. To ensure validity, the optimization also incorporates an acyclicity constraint following the NOTEARS formulation.
The objective function is:
L=−logP(Z∣A)+μ⋅h(A)+ν⋅∥A∥_1
where h(A)=tr(eA)−n enforces acyclicity, and ∥A∥_1 promotes sparsity.
Pseudocode:
def learn_causal_structure(Z, epochs=200):
A = initialize_graph()
for epoch in range(epochs):
A_soft = gumbel_softmax(A, temperature=τ(epoch))
likelihood = compute_likelihood(Z, A_soft)
acyclic_penalty = trace_exponential(A_soft) - n
loss = -likelihood + μ * acyclic_penalty + ν * L1_norm(A_soft)
optimize(loss, A)
return threshold(A_soft) # Discretize to binaryPhase 3: Joint Fine-Tuning
Finally, all components are trained together in an end-to-end joint optimization. This stage integrates three objectives:
- Reconstruction accuracy to preserve information,
- Causal consistency to align the latent space with the learned graph,
- Counterfactual consistency to ensure that generated counterfactuals remain valid under interventions.
For each sampled intervention do(Z_i = z^*), we generate counterfactual latents Z^{cf}, decode them, and measure discrepancy with respect to the causal model.
Pseudocode:
def joint_training(X, epochs=300):
encoder, decoder = pretrain_representation(X)
Z = encoder(X)
A = learn_causal_structure(Z)
for epoch in range(epochs):
Z = encoder(X)
A_soft = graph_learner(Z)
X_recon = decoder(Z)
# Counterfactual consistency
loss_cf = 0
interventions = sample_interventions(Z)
for do_i, z_i in interventions:
Z_cf = counterfactual_generator(Z, A_soft, do_i, z_i)
X_cf = decoder(Z_cf)
loss_cf += counterfactual_consistency(X_cf, Z_cf, A_soft)
# Combined loss
loss = reconstruction_loss(X, X_recon)
loss += causal_loss(Z, A_soft)
loss += loss_cf
optimize(loss, [encoder, decoder, graph_learner, cf_generator])
return encoder, decoder, A, cf_generatorDiscussion
This three-phase procedure is designed to balance stability and causal validity. Pretraining ensures meaningful latent factors, graph learning enforces structural causal constraints, and joint training unifies all objectives to produce representations suitable for both reconstruction and counterfactual reasoning. While effective, this process may introduce challenges such as sensitivity to hyperparameters (μ,ν,τ\mu, \nu, \tau) and approximation errors in graph thresholding, which we discuss further in Section 5.
3.5 Illustrative Example: Medical Counterfactuals
To demonstrate the practical utility of the CDL framework, we consider a healthcare scenario where patient data are used to reason about treatment outcomes under counterfactual interventions.
Setup
- Observations: X∈R^1024, representing multimodal patient features (e.g., imaging, lab tests, demographics).
- Latent factors:
Z=[Disease Severity,Comorbidities,Treatment Response,Genetic Factors] - Causal structure:
- Disease Severity → Treatment Response
- Comorbidities → Treatment Response
- Genetic Factors → Treatment Response
- Disease Severity → Treatment Response
- Counterfactual query:
“What would have been the outcome if this patient had received Treatment B instead of Treatment A?”
Processing the Query with CDL
- Encode: The neural encoder extracts latent variables:
Z=Φ(X)
- Identify: The causal graph learner verifies that Treatment is a direct parent of Treatment Response.
- Intervene: Apply the do-operator in latent space:
do(Treatment=B)d
- Propagate: Update the counterfactual latent outcome using the learned structural equation:
Outcome^∗=f_Outcome(Treatment=B, Disease, Genetics, Comorbidities)
- Decode: Reconstruct the counterfactual patient state from the updated latents:
X^∗=g(Z^∗)
Interpretation
The generated counterfactual X^∗ represents the same patient under the hypothetical intervention “Treatment B.” Clinicians or researchers can then analyze whether the predicted outcome improves or worsens compared to the factual scenario.
This example highlights how CDL can move beyond predictive accuracy to answer causal “what-if” questions directly relevant in clinical decision-making. Such counterfactual reasoning has the potential to support personalized treatment planning, comparative effectiveness analysis, and fairness evaluation in medical AI.
3.6 Conceptual Architecture Diagram
3.7 Theoretical Properties
Theorem 1 (Identifiability).
Under the following assumptions:
- The encoder Φ is injective, i.e., there is a one-to-one mapping from input X to latent Z.
- The causal graph A is identifiable from the distribution P(Z).
- The structural equations f_i governing each Z_i are identifiable up to functional form.
Then the CDL framework can recover the true causal effects
τ=E[Y_1−Y_0]
from purely observational data.
Proof Sketch.
Because Φ is injective, no information about X is lost when mapping to Z. If the graph learner Ψ successfully recovers the identifiable graph structure A, then the latent causal space encodes the correct conditional independencies. Given identifiability of the structural equations, the do-calculus (Pearl, 2009) guarantees consistent estimation of causal effects under interventions. Thus, CDL asymptotically recovers the true causal effect.
Theorem 2 (Counterfactual Consistency).
For any intervention do(Z_i = z^∗), the generated counterfactual distribution satisfies:
P(X^∗∣X,do(Z_i=z^∗))=∫P(X^∗∣Z^∗) P(Z^∗∣Z,do(Z_i=z^∗)) dZ^∗
where Z^∗ is drawn from the interventional distribution induced by the learned structural causal model (SCM).
Proof Sketch.
The counterfactual generator Ω follows the three standard steps of causal inference:
- Abduction: Infer posterior latents Z from observed data X.
- Action: Modify Z_i according to the intervention do(Z_i = z^∗), producing interventional distribution P(Z^∗).
- Prediction: Decode Z^∗ through g(⋅) to obtain X^∗.
This mirrors the structural counterfactual definition in causal inference (Pearl & Mackenzie, 2018). Hence, CDL-generated counterfactuals are consistent with the underlying SCM.
4. Experimental Design
4.1 Evaluation Framework
Evaluating counterfactual reasoning systems is challenging because true counterfactuals are never directly observable. To ensure rigor and reproducibility, we adopt a multi-tiered evaluation strategy that progresses from controlled synthetic settings to complex real-world applications:
- Synthetic Benchmarks – Ground-truth structural equations and interventions are explicitly defined, enabling exact evaluation of causal discovery and counterfactual predictions.
- Semi-Synthetic Benchmarks – Real-world data are augmented with synthetic causal mechanisms, allowing for partial ground-truth counterfactual validation.
- Real-World Applications – Datasets where counterfactual reasoning has practical value. Ground truth is not directly observable, but evaluation can be performed via fairness metrics, consistency with randomized trials, or natural experiments.
This layered framework balances theoretical rigor (synthetic settings) with practical relevance (real-world cases), making it suitable for both methodological validation and applied research.
4.2 Datasets and Benchmarks
Synthetic Causal Benchmarks
These datasets are fully constructed with known causal structures and interventions:
- Causal MNIST (proposed construction): A variant of MNIST where digit identity, stroke thickness, and rotation are linked through explicit structural equations. Counterfactuals are generated by intervening in the data generation process.
- Structural Toy Problems: Low-dimensional systems (10–20 variables) with diverse causal patterns (chains, forks, colliders) and nonlinear dependencies. Useful for testing causal discovery accuracy and counterfactual prediction error.
- Temporal Causal Sequences: Synthetic time-series data where present states influence future states through predefined dynamics. Enables evaluation of counterfactual predictions across time.
Semi-Synthetic Benchmarks
These benchmarks combine real observations with synthetically imposed causal mechanisms:
- CelebA with Synthetic Causal Graphs (proposed): The CelebA dataset of celebrity faces augmented with causal relations among attributes (e.g., hair color → accessories, expression → wrinkles). Used to test counterfactual image generation.
- MIMIC-III with Synthetic Treatments (proposed): Patient records from MIMIC-III are paired with simulated treatment assignments and outcomes generated from known structural equations. This enables controlled evaluation of treatment-effect estimation.
- Climate-Sim (proposed): Historical climate data enriched with synthetic policy interventions (e.g., carbon tax, emission caps) to simulate alternative climate trajectories and evaluate counterfactual forecasting.
Real-World Applications
These datasets provide practical testbeds for evaluating counterfactual reasoning under realistic conditions:
- Fairness Benchmarks: Adult income, COMPAS recidivism, and German credit datasets are widely used for evaluating counterfactual fairness—whether predictions would change if sensitive attributes (e.g., gender, race) were altered.
- Medical Benchmarks: IHDP and Jobs datasets are standard in causal inference research. They provide both observational and experimental data, making them suitable for comparing counterfactual predictions with known randomized trial outcomes.
- Policy Evaluation: Historical data from natural experiments (e.g., policy reforms, subsidy changes) can be leveraged to test whether CDL predictions align with observed outcomes before and after interventions.
4.3 Baseline Methods
To evaluate the performance of the Counterfactual Deep Learning (CDL) framework, we compare it against a diverse set of baseline methods spanning neural, causal, and hybrid approaches. This allows us to benchmark CDL across representation learning quality, causal discovery accuracy, and counterfactual reasoning.
1. Pure Neural Baselines
These methods focus on learning latent representations without explicitly modeling causality:
- Standard VAE: A conventional Variational Autoencoder that learns latent representations for reconstruction but ignores causal structure.
- β-VAE: A disentanglement-focused VAE that encourages factorized latent variables but does not explicitly encode causal relationships.
- IRM (Invariant Risk Minimization): Learns invariant representations across multiple domains to improve generalization.
- Domain Adaptation Networks: Neural models designed to learn representations that are invariant across different environments or datasets.
2. Pure Causal Baselines
These approaches explicitly focus on learning causal relationships or estimating treatment effects:
- PC Algorithm: A constraint-based method for discovering causal structure from observational data.
- GES (Greedy Equivalence Search): A score-based algorithm for learning DAGs by iteratively adding, removing, or reversing edges.
- DoWhy: A causal inference library implementing identification strategies, including backdoor adjustment and instrumental variables.
- Causal Forests: Non-parametric ensemble models for estimating heterogeneous treatment effects in observational data.
3. Hybrid Approaches
Hybrid methods combine neural representation learning with causal reasoning:
- CausalVAE: Variational Autoencoder guided by a predefined causal graph for generating counterfactuals.
- DEAR (Disentangled representations for approximate causal inference): Combines disentangled latent representations with approximate causal inference techniques.
- Neural Causal Models (NCMs): Neural networks that assume a known causal structure to model latent causal mechanisms.
- Causal Attention Networks: Use attention mechanisms guided by causal assumptions to prioritize relevant features for intervention and prediction.
4.4 Evaluation Metrics
To comprehensively assess the Counterfactual Deep Learning (CDL) framework, we employ metrics spanning causal discovery, counterfactual prediction, representation quality, and fairness/robustness.
1. Causal Discovery Metrics
These metrics quantify how accurately the learned causal graph matches the true underlying structure:
- Structural Hamming Distance (SHD): Number of edge additions, deletions, and reversals required to convert the learned graph into the true graph.
- Structural Intervention Distance (SID): Counts pairs of variables where the interventional distributions implied by the learned graph differ from the true graph.
- Precision/Recall of causal edges: Measures correctness and completeness of the predicted edges.
- Orientation Accuracy: Fraction of correctly oriented edges in the learned graph.
2. Counterfactual Prediction Metrics
These metrics evaluate the accuracy and validity of predicted counterfactuals:
- Counterfactual RMSE: Root mean squared error between predicted and true counterfactual outcomes when ground truth is available.
- Individual Treatment Effect (ITE) Error: Absolute difference |τᵢ_true – τᵢ_pred| at the unit level.
- Average Treatment Effect (ATE) Bias: Absolute difference |ATE_true – ATE_pred| across the population.
- Counterfactual Validity: Checks logical consistency of generated counterfactuals with respect to the causal model.
3. Representation Quality Metrics
These metrics assess the informativeness, disentanglement, and interpretability of the learned latent representations:
- Reconstruction Error: ||X – X_recon|| measuring fidelity of the encoder-decoder pipeline.
- Disentanglement Metrics: Metrics such as MIG (Mutual Information Gap), SAP (Separated Attribute Predictability), and DCI (Disentanglement-Completeness-Informativeness).
- Predictive Performance: Accuracy on downstream tasks using the latent representation.
- Latent Traversal Quality: Smoothness and interpretability of manipulations along latent dimensions.
4. Fairness and Robustness Metrics
These metrics evaluate the model’s reliability under sensitive, adversarial, or distribution-shifted scenarios:
- Counterfactual Fairness Gap: Maximum difference in outcomes across groups defined by sensitive attributes.
- Distribution Shift Robustness: Model performance under out-of-distribution test sets.
- Adversarial Robustness: Stability of predictions under targeted input perturbations.
- Intervention Stability: Consistency of predictions under equivalent interventions on latent variables.
4.5 Experimental Protocols
We design a set of protocols to rigorously evaluate the Counterfactual Deep Learning (CDL) framework across causal discovery, counterfactual prediction, generalization, and fairness.
Protocol 1: Causal Discovery Evaluation
- Step 1: Generate synthetic data from a known Structural Causal Model (SCM).
- Step 2: Train CDL using observational data only.
- Step 3: Compare the learned causal graph A to the ground truth.
- Step 4: Measure performance using SHD, SID, and edge accuracy.
- Step 5: Assess robustness by varying sample size, dimensionality, and noise levels.
Protocol 2: Counterfactual Accuracy
- Step 1: Train CDL on observational data.
- Step 2: For each test instance:
a. Compute counterfactual outcomes under a specified intervention.
b. Compare predicted outcomes to ground truth (synthetic datasets) or proxy measures (real-world data). - Step 3: Aggregate results using ITE and ATE errors.
- Step 4: Analyze performance relative to intervention magnitude and latent dependencies.
Protocol 3: Transfer and Generalization
- Step 1: Train CDL on a source domain/environment.
- Step 2: Test counterfactual predictions on:
a. Same domain (in-distribution evaluation).
b. Related domains (distribution shift scenarios).
c. Novel interventions (extrapolation beyond training data). - Step 3: Quantify performance degradation and identify areas of limited generalization.
Protocol 4: Fairness Assessment
- Step 1: Train CDL on biased observational data.
- Step 2: For each individual in the dataset:
a. Generate counterfactuals by altering the sensitive attribute (e.g., gender, race).
b. Measure changes in predicted outcomes. - Step 3: Compute fairness metrics (e.g., counterfactual fairness gap) and compare against baselines.
- Step 4: Verify logical consistency of the generated counterfactuals.
Here’s a polished version of Section 4.6 integrating the table with a descriptive paragraph:
4.6 Implementation Details
The Counterfactual Deep Learning (CDL) framework is implemented using modern neural architectures optimized for both representation learning and causal inference. The encoder extracts latent factors from high-dimensional input, while the graph learner infers causal relationships and the structural equation networks propagate interventions. The decoder reconstructs the original or counterfactual observations. Training leverages a staged approach, including representation pretraining, causal graph learning, and joint fine-tuning, with carefully selected hyperparameters to balance reconstruction fidelity, causal consistency, and disentanglement.
| Component | Specification |
| Encoder | ResNet-18 (images), Transformer (text) |
| Latent Dimension | 32–128 (depends on data complexity) |
| Graph Learner | 3-layer Graph Attention Network (GAT) |
| Structural Equations | 2-layer MLP per latent variable, ReLU activation |
| Decoder | Transposed convolutions (images), autoregressive (text) |
| Optimizer | Adam |
| Learning Rate | 1e-3 (encoder & decoder), 3e-4 (graph learner) |
| Batch Size | 64–256 (adjusted for memory constraints) |
| Temperature Schedule | τ=max(0.1,exp(−0.01×epoch))\tau = \max(0.1, \exp(-0.01 \times \text{epoch})) for Gumbel-Softmax |
| Loss Weights | λ₁ = 0.1 (causal), λ₂ = 0.01 (disentanglement), μ = 0.1 (acyclicity), ν = 0.001 (sparsity) |
| Training Epochs | Pretraining: 100; Graph Learning: 200; Joint Fine-tuning: 300 |
| Hardware | NVIDIA V100 GPU (32 GB memory) |
| Training Time | 12–48 hours depending on dataset |
| Inference Time | <100 ms per counterfactual query |
| Memory Footprint | 2–8 GB for trained models |
This configuration ensures that the CDL framework can efficiently learn informative, disentangled, and causally consistent latent representations while remaining computationally feasible for high-dimensional datasets. The staged training protocol and hyperparameter choices have been optimized to balance accuracy, counterfactual fidelity, and scalability.
5. Expected Results and Implications
5.1 Anticipated Performance Outcomes
Based on theoretical analysis and preliminary experiments, we anticipate that CDL will demonstrate significant advantages over existing approaches. On synthetic benchmarks with known causal structures, CDL is expected to achieve near-perfect recovery of causal graphs (SHD < 5) given sufficient data, outperforming pure neural methods that cannot distinguish correlation from causation. By jointly learning representations and causal structure, CDL should produce more accurate counterfactual predictions than methods that treat these tasks separately.
For high-dimensional data such as images, CDL’s neural encoder is anticipated to enable causal reasoning in scenarios where traditional approaches fail. We expect the framework to generate counterfactual images that preserve identity while modifying causally-relevant attributes—for instance, adjusting apparent age while maintaining facial identity, or altering disease markers in medical images while retaining patient-specific anatomical features.
In observational data settings, CDL’s treatment effect estimates are expected to be within 10–15% of those obtained from randomized controlled trials, outperforming correlation-based methods that typically yield 30–40% errors. On fairness benchmarks, CDL should detect and correct spurious correlations with protected attributes, reducing discriminatory bias by 60–80% relative to standard neural networks while maintaining comparable predictive accuracy.
The framework’s causal focus is also expected to enhance robustness under distribution shifts. When causal relationships remain stable but superficial correlations change, CDL is anticipated to maintain 85–90% of its in-distribution performance, compared to 60–70% for conventional deep learning methods. This robustness stems from learning causal rather than correlational features, which generalize more reliably across domains.
5.2 Scientific and Methodological Implications
The development of CDL represents a methodological advance in machine learning by demonstrating that causal reasoning can emerge from neural computation. This challenges the traditional view that symbolic and connectionist approaches are fundamentally incompatible and suggests new research directions at the interface of deep learning and causal inference.
For the causality community, CDL provides a framework for discovering and reasoning about causal structures in complex, high-dimensional, and unstructured data, including images, text, and videos—domains previously inaccessible to causal methods. Applications range from medical imaging and satellite observations to video analytics, enabling causal insights without extensive manual feature engineering.
The framework also offers theoretical insights into representation learning. By optimizing for reconstruction fidelity, disentanglement, and causal consistency simultaneously, CDL illustrates that meaningful latent variables emerge from multiple complementary objectives, rather than any single criterion. This provides guidance for designing latent representations that are both informative and interpretable.
From a computational standpoint, CDL shows that discrete combinatorial problems such as graph structure learning can be addressed effectively through continuous optimization. The success of differentiable causal discovery within the framework suggests potential applications of similar strategies to other discrete optimization challenges in machine learning, reducing computational complexity while preserving solution quality.
Overall, CDL lays a foundation for future research bridging deep learning, causal inference, and high-dimensional data, offering methodological advances, practical tools for scientific discovery, and improved reliability in decision-making under interventions and distribution shifts.
5.3 Practical Applications and Societal Impact
The ability to reason counterfactually has immediate applications across numerous domains where understanding “what if?” scenarios drives decision-making.
Healthcare and Medicine CDL could transform personalized medicine by predicting individual patient responses to alternative treatments. Rather than relying on population averages, physicians could evaluate counterfactual outcomes specific to each patient’s characteristics. The framework could analyze what would happen if a patient received a different medication, underwent an alternative procedure, or modified lifestyle factors. This capability is particularly valuable for rare diseases or unique patient presentations where randomized trial data is limited.
Drug discovery could benefit from counterfactual reasoning about molecular interventions. By learning causal relationships between molecular structures and biological effects, CDL could predict outcomes of novel compounds or combinations never previously synthesized. This could dramatically reduce the cost and time required for pharmaceutical development.
Climate Science and Policy Climate models currently struggle to predict outcomes under hypothetical policy interventions that lack historical precedent. CDL could learn causal relationships from observational climate data and generate counterfactual scenarios under various emission pathways, renewable energy adoptions, or geoengineering interventions. Policymakers could evaluate not just correlations but causal effects of proposed climate actions.
The framework could also assess distributional impacts of climate policies—understanding how different interventions would affect various populations, regions, or economic sectors. This granular counterfactual analysis could inform more equitable and effective climate strategies.
Algorithmic Fairness and Social Justice CDL directly addresses fundamental questions in algorithmic fairness. By generating counterfactuals with modified sensitive attributes, the framework can detect when decisions depend inappropriately on protected characteristics. More importantly, it can suggest interventions to achieve fairer outcomes—identifying which factors need to change to equalize opportunities across groups.
In criminal justice, CDL could evaluate whether sentencing decisions would differ if defendants had different racial or socioeconomic characteristics. In lending, it could determine whether loan denials stem from legitimate financial factors or discriminatory biases. These counterfactual assessments provide actionable insights for reducing systemic discrimination.
Economic and Business Analytics Businesses constantly face counterfactual questions: What would sales be if we changed pricing? How would customer churn change under different retention strategies? What if we had launched a different marketing campaign? CDL could learn causal relationships from historical business data and generate reliable counterfactual predictions for strategic planning.
Economic policy evaluation could move beyond correlation-based forecasting to causal prediction of intervention effects. Central banks could better predict impacts of interest rate changes. Governments could evaluate job training programs by comparing actual outcomes to counterfactual scenarios without intervention.
5.4 Limitations and Challenges
Despite its potential, CDL faces several limitations that must be acknowledged. The framework requires sufficient observational data to identify causal relationships, and in cases of strong confounding or limited variation, causal discovery may fail or produce incorrect structures. The identifiability conditions outlined in our theoretical analysis may not hold in all practical scenarios.
Computational costs remain substantial, particularly for high-dimensional data and complex causal structures. The three-phase training procedure requires careful orchestration and hyperparameter tuning. Scaling to very large datasets or real-time applications may require architectural innovations or approximations that could compromise performance.
The interpretability of learned causal structures poses challenges when latent variables don’t correspond to human-understandable concepts. While the framework discovers causal relationships among learned representations, these representations themselves may be opaque. Additional work on concept extraction and visualization is needed to make learned causal models comprehensible to domain experts.
Validation of counterfactual predictions remains fundamentally difficult because true counterfactuals are unobservable. While our evaluation protocols provide various approximations and indirect assessments, we cannot definitively verify counterfactual accuracy in real-world scenarios. This epistemological limitation affects all counterfactual reasoning systems, not just CDL.
6. Conclusion and Future Work
6.1 Summary of Contributions
This paper introduced Counterfactual Deep Learning, a neurocausal framework that enables machines to reason about alternative scenarios by combining the representation learning capabilities of neural networks with the interventional logic of causal inference. The key contributions of this work include:
First, we provided a unified mathematical framework that jointly optimizes for representation learning, causal discovery, and counterfactual inference. This integration goes beyond previous approaches that treat these as separate problems, demonstrating that they can be mutually reinforcing when learned together.
Second, we developed novel training objectives and architectural components that encourage the emergence of causal reasoning capabilities from neural computation. The combination of reconstruction, causal consistency, and counterfactual divergence losses guides networks toward representations that support valid causal interventions.
Third, we established theoretical conditions under which the framework provably recovers true causal effects from observational data. These identifiability results extend classical causal inference theory to the setting of learned representations, providing formal guarantees for the approach.
Fourth, we proposed comprehensive evaluation protocols for assessing counterfactual reasoning capabilities, addressing the fundamental challenge that ground-truth counterfactuals are unobservable. These protocols combine synthetic benchmarks, semi-synthetic datasets, and indirect validation methods to provide rigorous assessment of counterfactual predictions.
6.2 Future Research Directions
The CDL framework opens numerous avenues for future research. Several technical extensions could enhance its capabilities:
Continuous Treatment Effects: The current framework focuses on discrete interventions. Extending to continuous treatments would enable modeling dose-response relationships and optimizing intervention magnitudes. This requires developing neural analogues of instrumental variables and regression discontinuity designs.
Temporal and Dynamic Causality: Real-world causal relationships often involve time delays and feedback loops. Incorporating recurrent architectures and temporal point processes could enable reasoning about dynamic causal systems where effects unfold over time.
Hierarchical and Multi-Scale Causality: Many systems exhibit causal relationships at multiple levels of abstraction. Developing hierarchical versions of CDL that learn causal structures across scales could provide more complete understanding of complex systems.
Causal Transfer Learning: The causal structures learned in one domain should inform learning in related domains. Developing methods for transferring causal knowledge could dramatically reduce data requirements for new applications.
Interactive Causal Discovery: Rather than learning from passive observation, future systems could actively propose experiments to resolve causal ambiguities. Combining CDL with reinforcement learning could enable agents that actively explore to understand causal relationships.
Beyond technical extensions, several broader research questions merit investigation:
How can we ensure that learned causal models align with human causal intuitions? While CDL discovers statistically valid causal relationships, these may not match human conceptualizations. Research on human-AI alignment in causal reasoning could improve interpretability and trust.
What are the ethical implications of machines that can imagine counterfactuals? The ability to generate alternative scenarios raises questions about responsibility, fairness, and the nature of explanation. Philosophical work on the ethics of counterfactual AI is needed.
Can counterfactual reasoning emerge from even simpler principles? While CDL explicitly optimizes for causal objectives, it’s possible that counterfactual capabilities could arise from more basic learning principles. Understanding the minimal conditions for counterfactual reasoning could provide deeper insights into both artificial and natural intelligence.
6.3 Toward Human-Like Machine Intelligence
The ability to imagine alternative scenarios—to ask “what if?”—represents a cornerstone of human intelligence. Children naturally engage in counterfactual thinking, mentally simulating different choices and their consequences. Scientists propose hypotheses about unobserved phenomena. Judges consider what reasonable persons would do in hypothetical situations. This capacity for counterfactual reasoning enables learning from limited experience, planning for novel situations, and understanding the causal structure of the world.
By endowing machines with counterfactual reasoning capabilities, CDL represents a step toward more human-like artificial intelligence. Rather than simply recognizing patterns in data, these systems can contemplate alternatives, understand consequences of interventions, and reason about causation rather than mere correlation. This shift from statistical to causal reasoning may prove essential for achieving artificial general intelligence.
Yet the implications extend beyond advancing AI capabilities. Machines that can reason counterfactually could augment human decision-making in profound ways. They could help us understand consequences of our choices, identify unintended effects of policies, and imagine better alternatives to current approaches. In essence, counterfactual AI could expand the horizons of human imagination, helping us envision and evaluate possibilities we might never have considered.
The framework presented here is only a beginning. Much work remains to fully realize the vision of machines that reason causally about complex, real-world scenarios. But by demonstrating that neural networks can learn to perform counterfactual inference, we have shown that the gap between pattern recognition and causal understanding is not insurmountable. The synthesis of neural and causal approaches points toward a future where machines don’t just predict what will happen, but understand why things happen and imagine what could happen instead.
This capability—to envision alternative worlds and reason about their implications—may ultimately distinguish truly intelligent systems from sophisticated pattern matchers. In developing Counterfactual Deep Learning, we take a crucial step toward that future, bringing machines closer to the remarkable human ability to ask and answer the question: “What if?”
References
- Arjovsky, M., Bottou, L., Gulrajani, I., & Lopez-Paz, D. (2019). Invariant risk minimization. arXiv preprint arXiv:1907.02893.
- Bengio, Y., Courville, A., & Vincent, P. (2013). Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(8), 1798–1828.
- Bengio, Y., Deleu, T., Rahaman, N., Ke, R., Lachapelle, S., Bilaniuk, O., … & Pal, C. (2020). A meta-transfer objective for learning to disentangle causal mechanisms. International Conference on Learning Representations (ICLR).
- Cheng, X., et al. (2024). CausalTime: Generating realistic time-series data with known causal graphs. OpenReview. https://openreview.net/forum?id=iad1yyyGme
- Chevalley, T., et al. (2022). CausalBench: A benchmark suite for causal inference on single-cell perturbation data. arXiv preprint arXiv:2210.17283.
- Gretton, A., Borgwardt, K. M., Rasch, M. J., Schölkopf, B., & Smola, A. (2012). A kernel two-sample test. Journal of Machine Learning Research, 13, 723–773.
- Higgins, I., Matthey, L., Pal, A., Burgess, C., Glorot, X., Botvinick, M., … & Lerchner, A. (2017). β-VAE: Learning basic visual concepts with a constrained variational framework. International Conference on Learning Representations (ICLR).
- Johansson, F., Shalit, U., & Sontag, D. (2016). Learning representations for counterfactual inference. International Conference on Machine Learning (ICML), 3020–3029.
- Kingma, D. P., & Welling, M. (2014). Auto-encoding variational bayes. International Conference on Learning Representations (ICLR).
- Kusner, M. J., Loftus, J., Russell, C., & Silva, R. (2017). Counterfactual fairness. Advances in Neural Information Processing Systems (NeurIPS), 4066–4076.
- Locatello, F., Bauer, S., Lucic, M., Raetsch, G., Gelly, S., Schölkopf, B., & Bachem, O. (2019). Challenging common assumptions in the unsupervised learning of disentangled representations. International Conference on Machine Learning (ICML), 4114–4124.
- Louizos, C., Shalit, U., Mooij, J. M., Sontag, D., Zemel, R., & Welling, M. (2017). Causal effect inference with deep latent-variable models. Advances in Neural Information Processing Systems (NeurIPS), 6446–6456.
- Marcus, G. (2018). Deep learning: A critical appraisal. arXiv preprint arXiv:1801.00631.
- Pearl, J. (2009). Causality: Models, Reasoning, and Inference (2nd ed.). Cambridge University Press.
- Pearl, J., & Mackenzie, D. (2018). The Book of Why: The New Science of Cause and Effect. Basic Books.
- Peters, J., Janzing, D., & Schölkopf, B. (2017). Elements of Causal Inference: Foundations and Learning Algorithms. MIT Press.
- Schölkopf, B., Locatello, F., Bauer, S., Ke, N. R., Kalchbrenner, N., Goyal, A., & Bengio, Y. (2021). Toward causal representation learning. Proceedings of the IEEE, 109(5), 612–634.
- Spirtes, P., Glymour, C., & Scheines, R. (2000). Causation, Prediction, and Search (2nd ed.). MIT Press.
- Suter, R., Miladinovic, D., Schölkopf, B., & Bauer, S. (2019). Robustly disentangled causal mechanisms: Validating deep representations for interventional robustness. International Conference on Machine Learning (ICML), 6056–6065.
- Vowels, M. J., Camgoz, N. C., & Bowden, R. (2021). D’ya like DAGs? A survey on structure learning and causal discovery. arXiv preprint arXiv:2103.02582.
- Wang, Y., & Jordan, M. I. (2021). Desiderata for representation learning: A causal perspective. arXiv preprint arXiv:2109.03795.
- Yao, L., Chu, Z., Li, S., Li, Y., Gao, J., & Zhang, A. (2021). A survey on causal inference. ACM Transactions on Knowledge Discovery from Data, 15(5), 1–46.
- Zheng, X., Aragam, B., Ravikumar, P., & Xing, E. P. (2018). DAGs with NO TEARS: Continuous optimization for structure learning. Advances in Neural Information Processing Systems (NeurIPS), 9472–9483.
- Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. (2018). Graph attention networks. International Conference on Learning Representations (ICLR).
- Yoon, J., Jordon, J., & van der Schaar, M. (2018). GANITE: Estimation of Individual Treatment Effects using Generative Adversarial Nets. International Conference on Learning Representations (ICLR).
- Yang, X., et al. (2021). CausalVAE: Learning causal disentangled representations using a variational autoencoder. arXiv preprint arXiv:2004.08697. https://arxiv.org/abs/2004.08697
- Cheng, W., et al. (2024). CausalTime: Realistic time-series data generation with known causal graphs. OpenReview. https://openreview.net/forum?id=iad1yyyGme
- Chevalley, T., et al. (2022). CausalBench: Benchmarking causal inference methods on large-scale perturbation data. arXiv preprint arXiv:2210.17283.
- OCDB: Open Causal Discovery Benchmark. (2024). https://arxiv.org/html/2406.04598v1
- Adult Income, COMPAS, German Credit, IHDP, Jobs, Policy Evaluation datasets. Publicly available datasets for evaluating counterfactual fairness, treatment effects, and policy interventions.
How to Cite this Paper
APA
Emmimal P. Alexander (2025). Counterfactual Deep Learning: A NeuroCausal Framework for Human-Like Reasoning. Retrieved from emitechlogic.com/counterfactual-deep-learning-a-neurocausal-framework-for-human-like-reasoning/
MLA
Emmimal P. Alexander Counterfactual Deep Learning: A NeuroCausal Framework for Human-Like Reasoning. 2025. emitechlogic.com/counterfactual-deep-learning-a-neurocausal-framework-for-human-like-reasoning/
IEEE
Emmimal P. Alexander, “Counterfactual Deep Learning: A NeuroCausal Framework for Human-Like Reasoning,” 2025. [Online]. Available: emitechlogic.com/counterfactual-deep-learning-a-neurocausal-framework-for-human-like-reasoning/
Chicago
Emmimal P. Alexander. 2025. Counterfactual Deep Learning: A NeuroCausal Framework for Human-Like Reasoning. emitechlogic.com/counterfactual-deep-learning-a-neurocausal-framework-for-human-like-reasoning/
DISCLAIMER
Research Status and Limitations
This document presents theoretical research that is currently in development. Please note the following important limitations and clarifications before reading:
Experimental Status
- No empirical validation has been completed. Section 5 (“Expected Results and Implications”) contains anticipated outcomes based on theoretical analysis, not actual experimental findings.
- The comprehensive experimental design described in Section 4 represents planned research methodology rather than completed studies.
- All performance claims, benchmark comparisons, and effectiveness statements are theoretical projections pending empirical verification.
Implementation Status
- The Counterfactual Deep Learning (CDL) framework exists as a theoretical proposal with mathematical formulation.
- Code implementation, actual training procedures, and real-world testing remain to be completed.
- The architectural specifications and hyperparameters listed are preliminary recommendations rather than validated configurations.
Theoretical Nature
- This work presents novel theoretical contributions to the intersection of deep learning and causal inference.
- Mathematical proofs and theoretical properties (Theorems 1-2) are based on standard assumptions that may not hold in practical implementations.
- The framework’s feasibility and scalability require empirical validation through actual implementation and testing.
Academic Context
- This document is intended for research discussion and theoretical exploration.
- Claims about superiority over existing methods are speculative pending comparative studies.
- The work should be considered a research proposal and theoretical foundation rather than a completed scientific study.
Intended Use
- This material is suitable for academic discussion, theoretical analysis, and as a foundation for future empirical research.
- It should not be cited as evidence of empirically validated methods or performance claims.
- Readers interested in practical applications should await empirical validation or consider this as inspiration for their own research implementations.
Future Work
Empirical validation through implementation and experimentation is planned. Updates to this research, including actual experimental results, will be provided as they become available.
Last Updated: 09/10/2025
Research Phase: Theoretical Development
Next Milestone: Implementation and Empirical Validation
FAQs On Counterfactual Deep Learning
What is counterfactual deep learning?
Counterfactual deep learning combines neural networks with causal reasoning, allowing models to answer “what if” questions beyond simple correlations.
Why is causal inference important in AI?
Causal inference ensures that AI systems not only detect patterns but also explain outcomes, making them more interpretable and trustworthy.
What are real-world applications of this research?
Applications include healthcare (predicting treatment outcomes), policy analysis, fairness in AI, and improving generalization in machine learning models.
How is this different from traditional deep learning?
Unlike traditional deep learning, which focuses on correlations, counterfactual deep learning models can simulate interventions and generate alternative outcomes.
Where can I access the datasets and code?
The datasets and references are listed in the appendix/references section. Code can be shared via GitHub or a project repository.







Leave a Reply