Complete Guide to Find GCD in Python
Learn 7 different ways to find Greatest Common Divisor in Python. Perfect for beginners with simple explanations and interactive examples!
What You’ll Learn Today
What is GCD (Greatest Common Divisor)?
Think of GCD like finding the biggest puzzle piece that fits into two different puzzles. The Greatest Common Divisor is the largest number that can divide two numbers without leaving any remainder.
Simple Example:
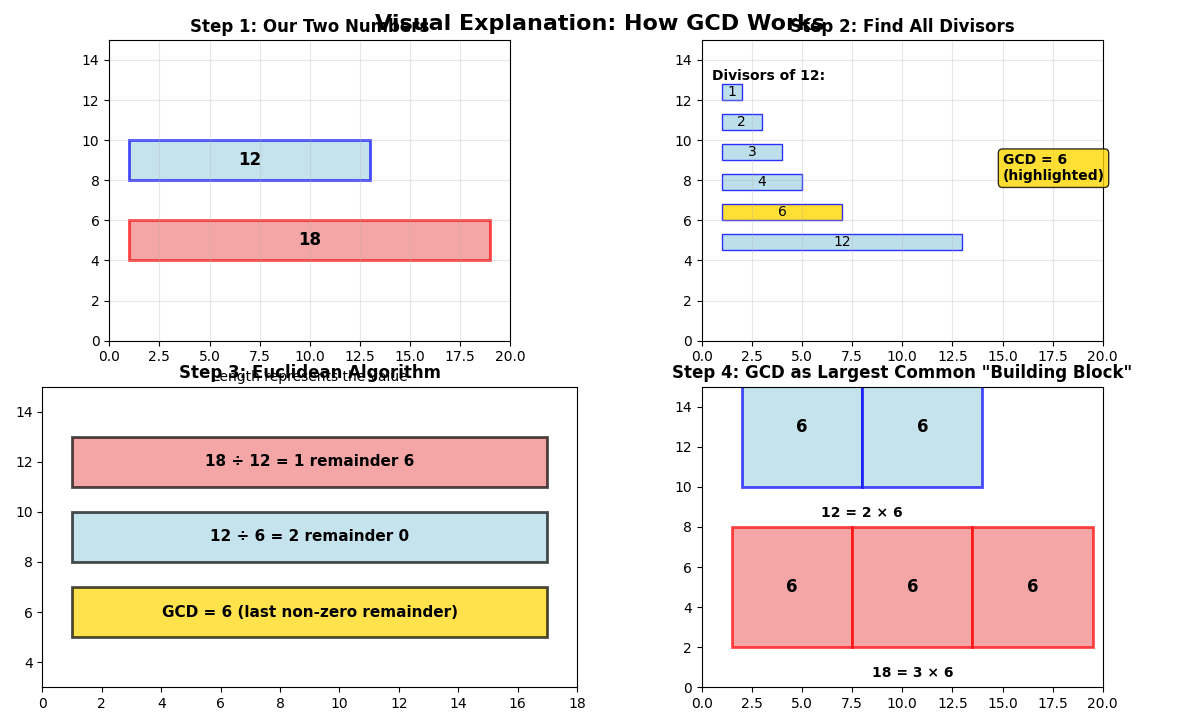
What’s the GCD of 12 and 18?
- Numbers that divide 12: 1, 2, 3, 4, 6, 12
- Numbers that divide 18: 1, 2, 3, 6, 9, 18
- Common divisors: 1, 2, 3, 6
- Greatest Common Divisor: 6
Why Should You Care About GCD?
In Programming:
- Simplifying fractions
- Building algorithms
- Solving math problems
In Real Life:
- Dividing things equally
- Planning schedules
- Security systems
Definition of GCD
The Greatest Common Divisor of two integers is the largest positive integer that divides both numbers evenly. In mathematical terms, if we have two numbers a and b, their GCD is the largest number d such that d divides a and d divides b.
Real-world Applications of GCD
GCD isn’t just a math concept. It’s used everywhere:
- Cryptography: RSA encryption relies heavily on GCD calculations
- Music: Finding rhythmic patterns and beats
- Graphics: Pixel arrangements and screen resolutions
- Engineering: Gear ratios and mechanical systems
Importance of GCD in Number Theory and Programming
Understanding GCD helps you grasp fundamental concepts in:
- Algorithm efficiency and optimization
- Mathematical problem solving
- Data structure design
- Competitive programming challenges
Method 1: Using Python’s Built-in math.gcd()
The easiest way to find GCD in Python is using the built-in function. It’s like having a calculator that already knows how to do the hard work for you!
Basic Syntax
import math
# Find GCD of two numbers
result = math.gcd(number1, number2)Step-by-Step Example
Let’s find the GCD of 48 and 18:
# Step 1: Import the math module
import math
# Step 2: Define our numbers
num1 = 48
num2 = 18
# Step 3: Find GCD using math.gcd()
gcd_result = math.gcd(num1, num2)
# Step 4: Print the result
print(f"GCD of {num1} and {num2} is: {gcd_result}")
# Output: GCD of 48 and 18 is: 6Expected Output:
GCD of 48 and 18 is: 6
More Examples
import math
# Example 1: Small numbers
print(math.gcd(12, 8)) # Output: 4
# Example 2: Large numbers
print(math.gcd(1071, 462)) # Output: 21
# Example 3: One number is multiple of another
print(math.gcd(15, 5)) # Output: 5
# Example 4: Prime numbers
print(math.gcd(13, 17)) # Output: 1Important Notes:
- math.gcd() only works with two numbers at a time
- Both numbers must be integers
- It automatically handles negative numbers
- Perfect for beginners learning Python basics
Syntax of math.gcd()
math.gcd(a, b)
# Parameters:
# a, b: integers (can be positive, negative, or zero)
# Returns:
# int: The greatest common divisor of a and bLimitations of math.gcd() in Python
Keep These in Mind:
- Only works with two integers: Can’t directly find GCD of multiple numbers
- Integer requirement: Won’t work with floating-point numbers
- No custom algorithms: You can’t modify how it calculates GCD
Practice Time: Try It Yourself!
Use the interactive Python playground below to practice finding GCD with different numbers.
Challenge Yourself:
- 1. Find GCD of 24 and 36
- 2. Find GCD of 100 and 75
- 3. What happens with GCD of 7 and 11?
Method 2: Euclidean Algorithm (The Smart Way)
The Euclidean Algorithm is like a magic trick. It finds GCD super fast using a simple pattern. Don’t worry – it sounds fancy but it’s actually pretty simple!
What is the Euclidean Algorithm for GCD?
The Euclidean Algorithm is one of the oldest algorithms in mathematics. It was described by the Greek mathematician Euclid around 300 BC. The algorithm is based on a simple principle: the GCD of two numbers doesn’t change if the larger number is replaced by its difference with the smaller number.
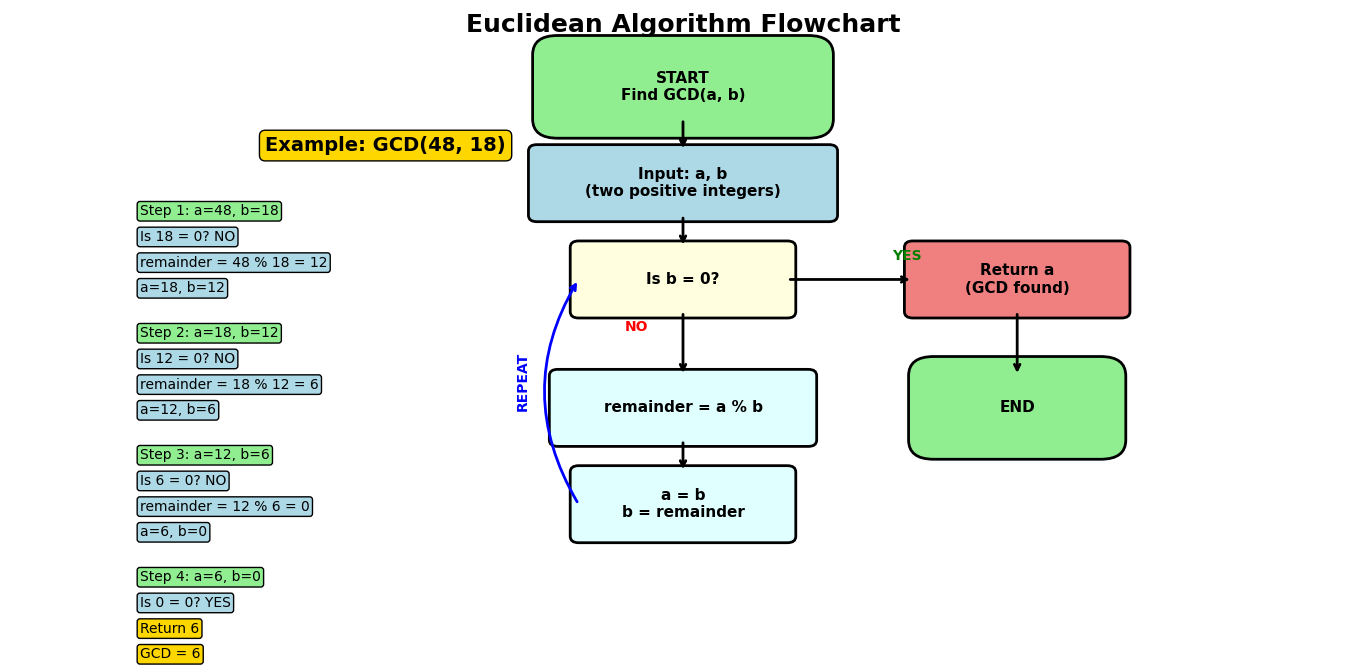
How It Works:
- Divide the bigger number by the smaller number
- Take the remainder
- Replace the bigger number with the smaller number
- Replace the smaller number with the remainder
- Repeat until remainder is 0
Step-by-Step Logic Breakdown
Finding GCD of 48 and 18:
Step 1: 48 ÷ 18 = 2 remainder 12 Step 2: 18 ÷ 12 = 1 remainder 6 Step 3: 12 ÷ 6 = 2 remainder 0 Answer: GCD is 6 (last non-zero remainder)
Python Implementation of Euclidean Algorithm
def gcd_euclidean(a, b):
"""
Find GCD using Euclidean Algorithm
This is super efficient!
"""
# Keep going until b becomes 0
while b:
# This line does the magic:
# a becomes b, b becomes remainder of a÷b
a, b = b, a % b
# When b is 0, a contains our GCD
return a
# Test it out
num1 = 48
num2 = 18
result = gcd_euclidean(num1, num2)
print(f"GCD of {num1} and {num2} = {result}")
# Output: GCD of 48 and 18 = 6Expected Output:
GCD of 48 and 18 = 6
Code Explanation with Detailed Walkthrough
# Detailed step-by-step execution
def gcd_euclidean_detailed(a, b):
print(f"Finding GCD of {a} and {b}")
step = 1
while b:
remainder = a % b
print(f"Step {step}: {a} ÷ {b} = {a//b} remainder {remainder}")
a, b = b, remainder
step += 1
print(f"Final answer: {a}")
return a
# Run the detailed version
gcd_euclidean_detailed(48, 18)Expected Output:
Finding GCD of 48 and 18 Step 1: 48 ÷ 18 = 2 remainder 12 Step 2: 18 ÷ 12 = 1 remainder 6 Step 3: 12 ÷ 6 = 2 remainder 0 Final answer: 6
Why This Method Rocks:
- Super fast even with huge numbers
- Used in advanced algorithms
- Works great with while loops
- Essential for understanding number theory
Method 3: Brute Force (The Simple Way)
Sometimes the simplest approach is the best for learning. The brute force method checks every possible number to find the GCD. It’s like checking every key to see which one opens the lock!
How Brute Force Works
- Find the smaller of the two numbers
- Start from that number and go down to 1
- Check if the number divides both original numbers
- The first number that works is our GCD!
Python Implementation
def gcd_brute_force(a, b):
"""
Find GCD by checking all possible divisors
Easy to understand but slower for big numbers
"""
# Find the smaller number
smaller = min(a, b)
# Start from the smaller number and go down
for i in range(smaller, 0, -1):
# Check if i divides both numbers
if a % i == 0 and b % i == 0:
# Found our GCD!
return i
# This should never happen with positive integers
return 1
# Test the function
num1 = 24
num2 = 36
result = gcd_brute_force(num1, num2)
print(f"GCD of {num1} and {num2} = {result}")
# Output: GCD of 24 and 36 = 12Expected Output:
GCD of 24 and 36 = 12
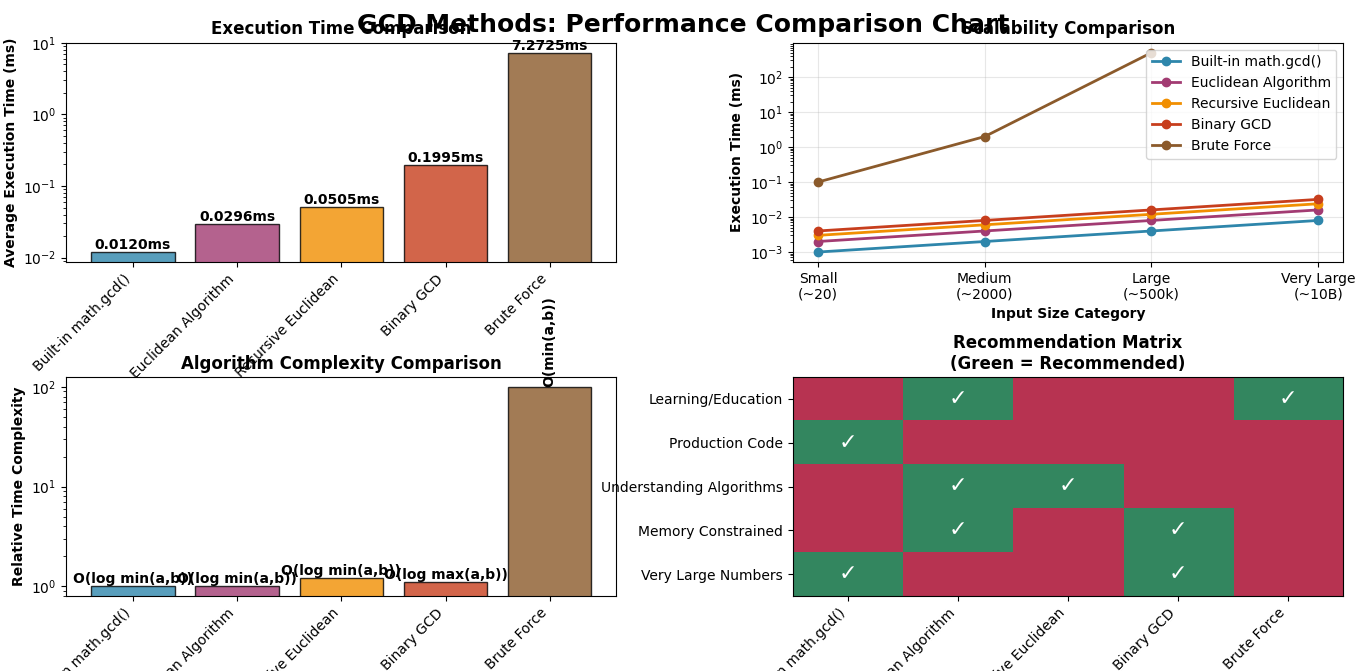
Performance Comparison: Brute Force vs Euclidean Algorithm
Pros:
- Very easy to understand
- Great for learning logical concepts
- No complex math needed
Cons:
- Very slow for large numbers
- Inefficient algorithm
- Not suitable for production code
Time Complexity Analysis
Understanding why different methods have different speeds:
- Brute Force: O(min(a,b)) – checks every number from smallest down to 1
- Euclidean Algorithm: O(log(min(a,b))) – much faster because it eliminates numbers quickly
- Built-in math.gcd(): Uses optimized Euclidean algorithm internally
Compare Different Methods
Try implementing both brute force and Euclidean methods with the same numbers and see which one you prefer!
Challenge Yourself:
- 1. Compare speed with numbers 1000 and 750
- 2. Test with prime numbers like 17 and 19
- 3. See what happens with identical numbers
Method 4: Recursive Approach to Find GCD
Recursion is when a function calls itself. It’s like looking into a mirror that reflects another mirror! The recursive GCD method is elegant and demonstrates the mathematical beauty of the Euclidean algorithm.
Recursive Approach to Find GCD of Two Numbers
def gcd_recursive(a, b):
"""
Find GCD using recursion
This mirrors the mathematical definition beautifully
"""
if b == 0:
return a
else:
return gcd_recursive(b, a % b)
# Test the recursive function
num1 = 56
num2 = 42
result = gcd_recursive(num1, num2)
print(f"GCD of {num1} and {num2} = {result}")
# Output: GCD of 56 and 42 = 14Expected Output:
GCD of 56 and 42 = 14
Explanation with Stack Trace
Let’s trace through how the recursive calls work:
gcd_recursive(56, 42) ↓ a=56, b=42, so call gcd_recursive(42, 56%42) gcd_recursive(42, 14) ↓ a=42, b=14, so call gcd_recursive(14, 42%14) gcd_recursive(14, 0) ↓ a=14, b=0, so return 14 Final result: 14
Example with Step-by-Step Breakdown
def gcd_recursive_detailed(a, b, depth=0):
"""
Recursive GCD with detailed output
Shows exactly what happens at each step
"""
indent = " " * depth
print(f"{indent}gcd_recursive({a}, {b})")
if b == 0:
print(f"{indent}Base case reached: return {a}")
return a
else:
print(f"{indent}Calling gcd_recursive({b}, {a % b})")
result = gcd_recursive_detailed(b, a % b, depth + 1)
print(f"{indent}Returning {result}")
return result
# Run detailed version
print("Finding GCD of 48 and 18:")
gcd_recursive_detailed(48, 18)Expected Output:
Finding GCD of 48 and 18:
gcd_recursive(48, 18)
Calling gcd_recursive(18, 12)
gcd_recursive(18, 12)
Calling gcd_recursive(12, 6)
gcd_recursive(12, 6)
Calling gcd_recursive(6, 0)
gcd_recursive(6, 0)
Base case reached: return 6
Returning 6
Returning 6
Returning 6
Why Use Recursion for GCD?
- Mirrors the mathematical definition perfectly
- Very clean and readable code
- Great for understanding advanced programming concepts
- Demonstrates the power of divide-and-conquer algorithms
Things to Watch Out For:
- Can cause stack overflow with very large numbers
- Uses more memory than iterative version
- Slightly slower due to function call overhead
Method 5: Find GCD of Multiple Numbers
What if you need to find the GCD of more than two numbers? Python makes this easy with some clever tricks!
How to Find GCD of Multiple Numbers Using functools.reduce
from math import gcd
from functools import reduce
def find_gcd_list(numbers):
"""
Find GCD of a list of numbers
Uses reduce to apply gcd function repeatedly
"""
return reduce(gcd, numbers)
# Test with multiple numbers
numbers = [24, 36, 60, 12]
result = find_gcd_list(numbers)
print(f"GCD of {numbers} = {result}")
# Output: GCD of [24, 36, 60, 12] = 12Expected Output:
GCD of [24, 36, 60, 12] = 12
Example: GCD of [24, 36, 60]
Let’s see how this works step by step:
Step 1: gcd(24, 36) = 12 Step 2: gcd(12, 60) = 12 Final result: 12
Explanation of reduce() Usage
The reduce() function applies a function cumulatively to items in a sequence. Here’s how it works with GCD:
from math import gcd
def find_gcd_manual(numbers):
"""
Find GCD without using reduce - shows what reduce does internally
"""
if len(numbers) < 2:
return numbers[0] if numbers else 0
result = numbers[0]
for i in range(1, len(numbers)):
result = gcd(result, numbers[i])
print(f"Step {i}: gcd({result if i==1 else 'previous'}, {numbers[i]}) = {result}")
return result
# Test manual version
numbers = [48, 18, 24]
print(f"Finding GCD of {numbers}:")
result = find_gcd_manual(numbers)
print(f"Final GCD: {result}")Expected Output:
Finding GCD of [48, 18, 24]: Step 1: gcd(48, 18) = 6 Step 2: gcd(6, 24) = 6 Final GCD: 6
Cool Applications:
- Finding common factors in data analysis
- Simplifying complex fractions
- Solving scheduling problems with multiple constraints
- Working with arrays and lists in mathematical computations
Method 6: Find GCD and LCM in Python Together
GCD and LCM (Least Common Multiple) are best friends in mathematics. Once you know one, finding the other is super easy!
Mathematical Relationship Between GCD and LCM
The Magic Formula:
GCD(a,b) × LCM(a,b) = a × b
This means: LCM(a,b) = (a × b) ÷ GCD(a,b)
Code to Calculate Both Values
from math import gcd
def gcd_and_lcm(a, b):
"""
Calculate both GCD and LCM of two numbers
Uses the mathematical relationship between them
"""
# Calculate GCD first
gcd_value = gcd(a, b)
# Calculate LCM using the formula
lcm_value = abs(a * b) // gcd_value
return gcd_value, lcm_value
# Test the function
num1 = 12
num2 = 18
gcd_result, lcm_result = gcd_and_lcm(num1, num2)
print(f"Numbers: {num1} and {num2}")
print(f"GCD = {gcd_result}")
print(f"LCM = {lcm_result}")
print(f"Verification: {gcd_result} × {lcm_result} = {gcd_result * lcm_result}")
print(f"Original product: {num1} × {num2} = {num1 * num2}")Expected Output:
Numbers: 12 and 18 GCD = 6 LCM = 36 Verification: 6 × 36 = 216 Original product: 12 × 18 = 216
Practical Use Cases
GCD Applications:
- Simplifying fractions
- Finding common denominators
- Cryptographic algorithms
LCM Applications:
- Scheduling recurring events
- Finding common multiples
- Synchronizing processes
Applications of GCD in Real-World Python Projects
Where Is GCD Used in Programming?
Cryptography (RSA Algorithm)
GCD plays a crucial role in RSA encryption, one of the most widely used encryption methods:
from math import gcd
def is_coprime(a, b):
"""
Check if two numbers are coprime (GCD = 1)
Essential for RSA key generation
"""
return gcd(a, b) == 1
# Example: RSA requires coprime numbers
p, q = 61, 53 # Prime numbers
n = p * q # Public key component
phi = (p-1) * (q-1) # Euler's totient
# Choose e such that gcd(e, phi) = 1
e = 17
if is_coprime(e, phi):
print(f"e = {e} is valid for RSA")
print(f"gcd({e}, {phi}) = {gcd(e, phi)}")
else:
print(f"e = {e} is not valid for RSA")Simplifying Fractions
from math import gcd
def simplify_fraction(numerator, denominator):
"""
Simplify a fraction using GCD
"""
common_divisor = gcd(numerator, denominator)
simplified_num = numerator // common_divisor
simplified_den = denominator // common_divisor
return simplified_num, simplified_den
# Examples
fractions = [(12, 18), (24, 36), (15, 25)]
for num, den in fractions:
simple_num, simple_den = simplify_fraction(num, den)
print(f"{num}/{den} simplifies to {simple_num}/{simple_den}")Expected Output:
12/18 simplifies to 2/3 24/36 simplifies to 2/3 15/25 simplifies to 3/5
Scheduling and Time-based Calculations
from math import gcd
from functools import reduce
def find_sync_time(intervals):
"""
Find when multiple periodic events synchronize
Uses LCM which requires GCD
"""
def lcm(a, b):
return abs(a * b) // gcd(a, b)
return reduce(lcm, intervals)
# Example: When do these events align?
events = {
"Daily backup": 1, # Every 1 day
"Weekly report": 7, # Every 7 days
"Monthly audit": 30, # Every 30 days
}
intervals = list(events.values())
sync_day = find_sync_time(intervals)
print("Event synchronization:")
for event, interval in events.items():
print(f" {event}: every {interval} days")
print(f"\nAll events align every {sync_day} days")Common Mistakes While Finding GCD in Python
Avoiding Pitfalls When Implementing GCD Functions
Using Incorrect Loop Conditions
Wrong Way:
# This will miss the correct answer!
def gcd_wrong(a, b):
smaller = min(a, b)
for i in range(1, smaller): # Missing smaller itself!
if a % i == 0 and b % i == 0:
result = i
return resultCorrect Way:
# Start from smaller and go DOWN
def gcd_correct(a, b):
smaller = min(a, b)
for i in range(smaller, 0, -1): # Include smaller, go down to 1
if a % i == 0 and b % i == 0:
return i # Return immediately when found
return 1Forgetting Integer Division
Watch Out For:
- Using
/instead of//can give float results - Not handling negative numbers properly
- Forgetting to check for zero values
Not Handling Negative or Zero Values
def gcd_robust(a, b):
"""
Handle edge cases properly
"""
# Handle negative numbers
a, b = abs(a), abs(b)
# Handle zero cases
if a == 0:
return b
if b == 0:
return a
# Regular Euclidean algorithm
while b:
a, b = b, a % b
return a
# Test edge cases
test_cases = [(0, 5), (-12, 18), (15, -25), (-20, -30)]
for a, b in test_cases:
result = gcd_robust(a, b)
print(f"gcd({a}, {b}) = {result}")Testing GCD Programs in Python
How to Write Unit Tests for GCD Functions
Testing your code is crucial for making sure it works correctly. Here's how to test GCD functions:
import unittest
from math import gcd
class TestGCDFunctions(unittest.TestCase):
def test_basic_gcd(self):
"""Test basic GCD calculations"""
self.assertEqual(gcd(12, 18), 6)
self.assertEqual(gcd(48, 18), 6)
self.assertEqual(gcd(100, 75), 25)
def test_prime_numbers(self):
"""Test GCD of prime numbers"""
self.assertEqual(gcd(13, 17), 1)
self.assertEqual(gcd(7, 11), 1)
def test_identical_numbers(self):
"""Test GCD of identical numbers"""
self.assertEqual(gcd(15, 15), 15)
self.assertEqual(gcd(100, 100), 100)
def test_edge_cases(self):
"""Test edge cases"""
self.assertEqual(gcd(0, 5), 5)
self.assertEqual(gcd(7, 0), 7)
self.assertEqual(gcd(1, 100), 1)
# Run the tests
if __name__ == '__main__':
unittest.main()Sample Test Cases for Different GCD Methods
Essential Test Cases:
- Basic cases: gcd(12, 18) = 6
- Prime numbers: gcd(13, 17) = 1
- One divides other: gcd(15, 5) = 5
- Large numbers: gcd(1071, 462) = 21
- Edge cases: gcd(0, 5) = 5
Performance Tips for Calculating GCD in Python
Optimizing GCD Calculations for Large Numbers
Use Efficient Algorithms
For the best performance, always prefer these methods in order:
- math.gcd(): Fastest, optimized C implementation
- Euclidean Algorithm: Fast, easy to understand
- Recursive approach: Elegant but uses more memory
- Brute force: Only for learning, too slow for real use
Avoid Unnecessary Calculations
import time
from math import gcd
def benchmark_gcd_methods(a, b, iterations=10000):
"""
Compare performance of different GCD methods
"""
# Test built-in method
start = time.time()
for _ in range(iterations):
result = gcd(a, b)
builtin_time = time.time() - start
# Test Euclidean method
def gcd_euclidean(x, y):
while y:
x, y = y, x % y
return x
start = time.time()
for _ in range(iterations):
result = gcd_euclidean(a, b)
euclidean_time = time.time() - start
print(f"Built-in gcd(): {builtin_time:.4f} seconds")
print(f"Euclidean algorithm: {euclidean_time:.4f} seconds")
print(f"Speed difference: {euclidean_time/builtin_time:.2f}x")
# Test with large numbers
benchmark_gcd_methods(123456789, 987654321)Leverage Built-in Libraries Where Possible
Pro Tips:
- Always use
math.gcd()for production code - Implement custom algorithms only when learning
- Use
functools.reduce()for multiple numbers - Consider input validation for user-provided numbers
Test Your Knowledge: Interactive GCD Quiz
Let's see how well you understand GCD concepts! Click on the answers to check if you're correct.
Question 1: What is the GCD of 24 and 36?
Question 2: Which method is fastest for large numbers?
Question 3: What is the GCD of two prime numbers?
Question 4: What Python module contains the built-in gcd() function?
Question 5: In the Euclidean algorithm, when do we stop?
Frequently Asked Questions (FAQ)
Conclusion: Choose the Right GCD Method in Python
Congratulations! You've learned 7 different ways to find GCD in Python. Each method has its place and purpose in programming.
When to Use Built-in vs Custom Methods
Use math.gcd() when:
- Building production applications
- Working with large numbers
- You need maximum performance
- Simplicity is important
Use custom implementations when:
- Learning algorithms
- Technical interviews
- Understanding the math
- Educational purposes
Importance of Understanding the Logic Behind Each Method
Even though Python gives you ready-made tools, understanding how they work makes you a better programmer. The concepts you learned here apply to:
- Algorithm design and analysis
- Mathematical problem solving
- Optimization techniques
- Understanding complexity and efficiency
Encouragement to Try All Approaches
Don't stop here! Try implementing these methods with different inputs:
- Very large numbers (like 123456789 and 987654321)
- Small numbers (like 3 and 7)
- Numbers where one divides the other
- Lists of multiple numbers
Your GCD Journey Continues:
You now have the tools to tackle GCD problems with confidence. Keep practicing, and remember that the best way to learn programming is by doing. Try building a calculator that can find both GCD and LCM, or implement a fraction simplifier!
Want to explore more Python concepts? Check out our guides on string formatting and variable swapping techniques.
External Resources
For deeper learning about GCD algorithms and implementations, check out these additional resources:
- UpGrad's GCD Tutorial - Comprehensive guide with examples
- Programiz HCF Examples - More practice problems and solutions
- GeeksforGeeks GCD Article - Advanced techniques and optimizations




Leave a Reply