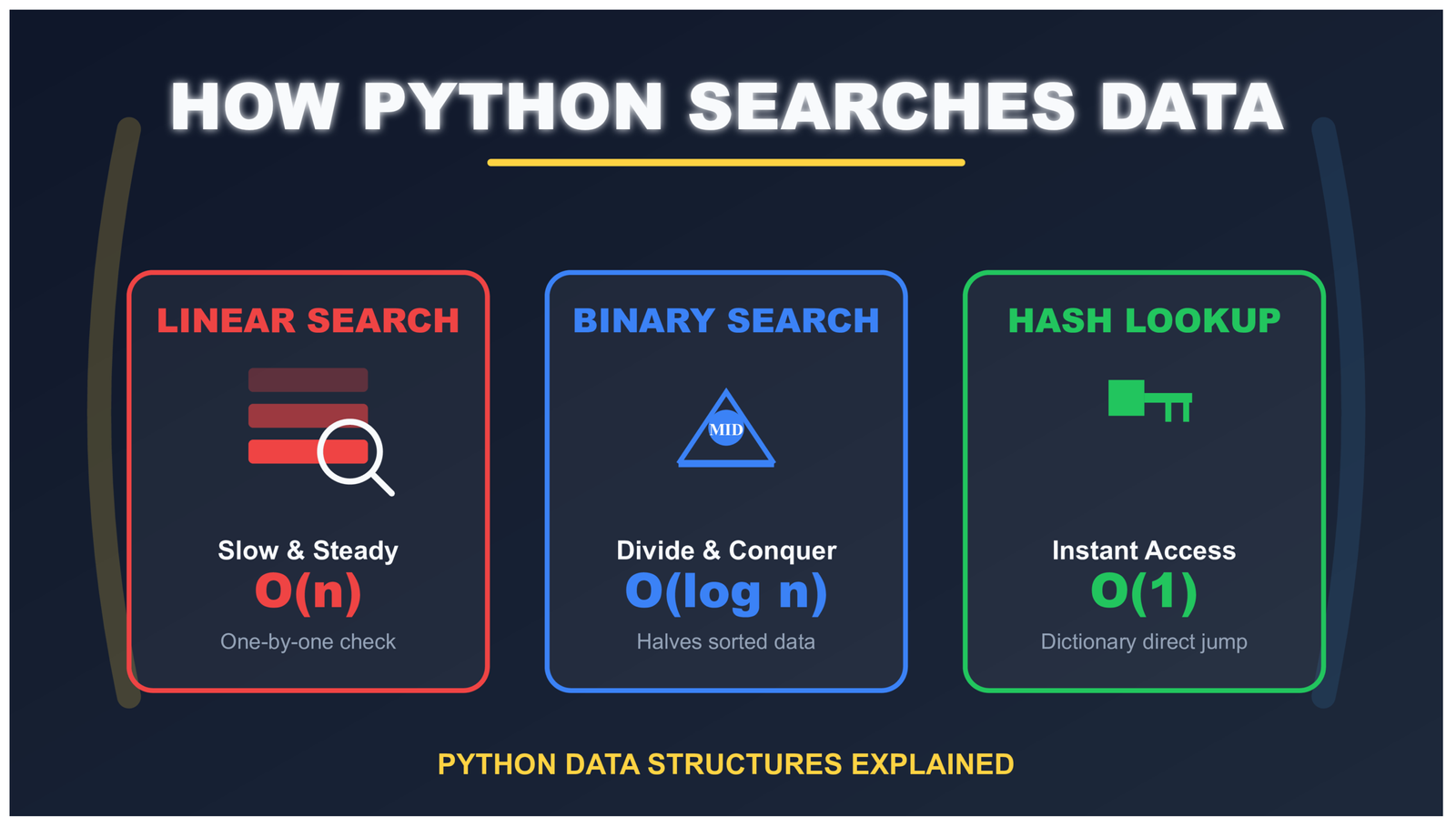
How Python Searches Data: Linear Search, Binary Search, and Hash Lookup

The Simple Code That Hides Three Different Search Methods

Let me show you something you probably write every day:

if user_id in active_users:
    grant_access()

See that word “in”? It looks simple. Just checking if something exists in a collection. You write it without thinking.

But here’s the interesting part: that tiny word makes Python search through your data. And depending on what type of collection you used (a list, a set, or a dictionary), Python searches in completely different ways.

Think of it like looking for a book. You can:

• Check every book on the shelf one by one (that’s linear search)
• If books are sorted alphabetically, jump to the middle and eliminate half the books at once (that’s binary search)
• Use a catalog that tells you exactly where the book is (that’s hash lookup)

Python does the same thing with your data. The search method depends on what kind of collection you chose when you wrote your code. Let’s understand how each method works, when to use them, and why it matters for your programs.

Why Understanding Search Methods Matters for Your Python Programs

Here’s something important: Python doesn’t automatically pick the fastest way to search your data. It can’t read your mind.

When you write x in my_collection, Python looks at one thing: what type is my_collection?

Is it a list? Python searches one way.
Is it a set? Python searches a different way.
Is it a dictionary? Python searches yet another way.

Let me show you with real examples:

# Example 1: Using a list
users_list = ["alice", "bob", "charlie"]
if "alice" in users_list:  # Python checks: bob? no. alice? yes!
    print("Found!")

# Example 2: Using a set
users_set = {"alice", "bob", "charlie"}
if "alice" in users_set:  # Python jumps directly to alice
    print("Found!")

Both examples do the same thing – they find “alice”. But the second one is much faster. Why? Because sets use a completely different search method than lists.

Here’s the speed difference:

• With a list: If you have 1,000,000 items, Python might check all 1,000,000 of them
• With a set: If you have 1,000,000 items, Python finds it in about 1 step

That’s not a small difference. That’s the difference between your program finishing instantly or taking several seconds. When you’re building real applications, this matters a lot.

Let’s learn about each search method so you can pick the right one for your programs. We’ll start with the simplest: linear search.

Linear Search in Python Lists: Checking Items One by One

Linear search is the simplest way to find something. Let me explain it like you’re looking for a friend in a line of people.

Imagine 10 people standing in a line. You’re looking for your friend Sarah. What do you do?

You start at the first person. “Are you Sarah?” No.
Move to the second person. “Are you Sarah?” No.
Move to the third person. “Are you Sarah?” Yes! Found her!

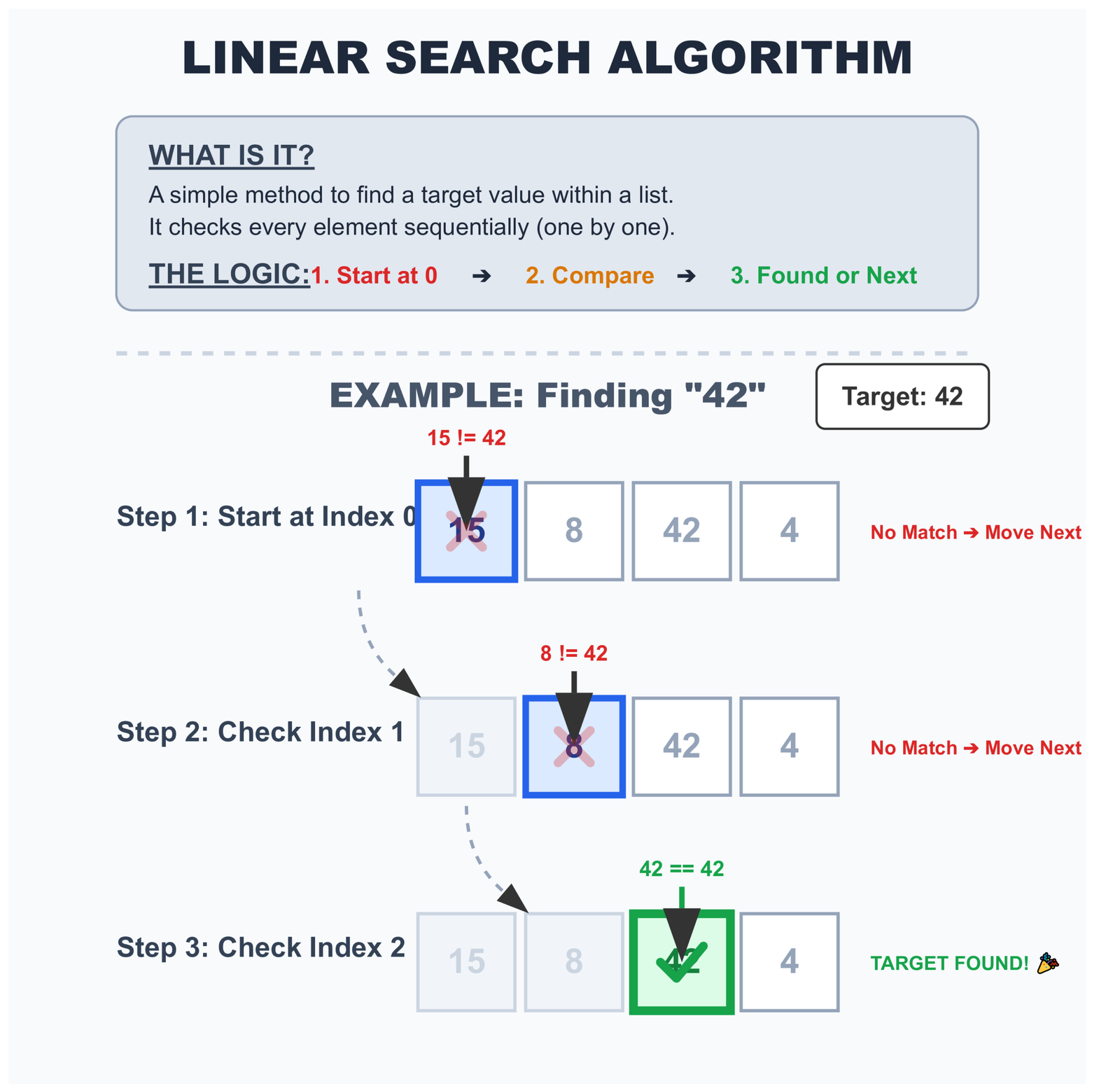
That’s exactly how linear search works. Python starts at the first item and checks each one until it finds what you’re looking for.

How Python Does Linear Search Step by Step

When you write x in my_list, here’s what Python does:

# Your code
numbers = [10, 25, 30, 45, 50]
search_for = 30

if search_for in numbers:
    print("Found it!")

# What Python actually does behind the scenes:
# Step 1: Check index 0 → Is 10 equal to 30? No
# Step 2: Check index 1 → Is 25 equal to 30? No
# Step 3: Check index 2 → Is 30 equal to 30? Yes! Found it!

Python doesn’t skip ahead. It doesn’t take shortcuts. It checks every single item in order until it finds a match or runs out of items.

Here’s the code that shows how linear search works:

def linear_search_explained(items, target):
    """Search for target in items, showing each step"""
    
    print(f"Looking for: {target}")
    print(f"Searching in: {items}")
    print()
    
    for index in range(len(items)):
        current_item = items[index]
        print(f"Step {index + 1}: Checking position {index} → {current_item}")
        
        if current_item == target:
            print(f"✓ Found {target} at position {index}!")
            return True
    
    print(f"✗ {target} not found in the list")
    return False

# Let's try it
numbers = [5, 12, 8, 30, 15]
linear_search_explained(numbers, 30)

# Output:
# Looking for: 30
# Searching in: [5, 12, 8, 30, 15]
#
# Step 1: Checking position 0 → 5
# Step 2: Checking position 1 → 12
# Step 3: Checking position 2 → 8
# Step 4: Checking position 3 → 30
# ✓ Found 30 at position 3!

Understanding How Many Checks Python Makes

The number of checks Python makes depends on where your item is located:

# Example list
fruits = ["apple", "banana", "cherry", "date", "elderberry"]

# Case 1: Item is first
if "apple" in fruits:  # Python checks 1 item - FAST!
    print("Found")

# Case 2: Item is in the middle
if "cherry" in fruits:  # Python checks 3 items - MEDIUM
    print("Found")

# Case 3: Item is last
if "elderberry" in fruits:  # Python checks 5 items - SLOWER
    print("Found")

# Case 4: Item doesn't exist
if "fig" in fruits:  # Python checks ALL 5 items - SLOWEST
    print("Found")

Let me show you the pattern with numbers:

• Best case: Item is first → 1 check (very lucky!)
• Average case: Item is somewhere in the middle → checks half the items
• Worst case: Item is last or doesn’t exist → checks every single item

This becomes important with large lists. Imagine you have a list of 100,000 user IDs. If the user you’re looking for is at the end, Python makes 100,000 comparisons. Every single time someone logs in!

That’s why understanding search methods matters. For small lists (10-20 items), you won’t notice the difference. But for large lists, the speed difference becomes huge.

How Python Optimizes Linear Search Without Changing the Algorithm

Python’s linear search runs in C, not pure Python. This seemingly small detail makes a surprisingly big difference.

Look at these two approaches:

# Writing your own search loop (slower)
def find_user_manual(user_id, user_list):
    for user in user_list:
        if user == user_id:
            return True
    return False

# Using Python's built-in (faster)
def find_user_builtin(user_id, user_list):
    return user_id in user_list

Both perform identical operations. Both check the same number of items. Yet the second version runs noticeably faster because:

• The C implementation bypasses Python’s interpreter overhead on each iteration
• Memory access patterns get optimized at the C level
• Type checking happens once instead of repeatedly

The algorithm hasn’t changed. The execution speed has. This is why using Python’s built-in functions matters more than you might think.

Why Linear Search Is Still Useful (Even Though It’s Slow)

You might be thinking: “If linear search is slow, why do we use it at all?”

Good question! The truth is, linear search is still the right choice in many situations. Let me explain why.

When Linear Search Is Actually the Best Choice

Reason 1: Your data is small

# Small list - linear search is fine
favorite_colors = ["red", "blue", "green", "yellow"]

if "blue" in favorite_colors:
    print("Blue is a favorite!")
    
# With only 4 items, Python checks at most 4 times
# This happens in microseconds - you'll never notice!

Reason 2: Your data isn’t sorted

# Unsorted data from user input
shopping_cart = []
shopping_cart.append("milk")
shopping_cart.append("eggs")
shopping_cart.append("bread")
shopping_cart.append("apples")

# Checking is easy
if "milk" in shopping_cart:
    print("Milk is in cart")
    
# If we sorted this list just to search faster,
# we'd waste time sorting when we only search once!

Reason 3: Your data changes frequently

# Chat room with users joining and leaving
active_users = []

# User joins
active_users.append("Alice")
active_users.append("Bob")

# User leaves
active_users.remove("Alice")

# User joins
active_users.append("Charlie")

# For data that changes a lot, keeping it sorted
# or in a dictionary might be more work than it's worth

Reason 4: The item you want is usually near the start

# Recent notifications (newest first)
notifications = [
    "New message from Alice",  # Just received
    "New email",                # 2 minutes ago
    "Calendar reminder",        # 5 minutes ago
    # ... older notifications
]

# When checking "New message from Alice"
# Linear search finds it on the first try!

The Simple Rule for When to Use Linear Search

Use linear search when:

• Your list has fewer than 100 items
• You’re only searching once or twice
• Your data isn’t sorted and sorting would take more time
• Your data changes frequently

Don’t use linear search when:

• Your list has thousands of items
• You’re searching many times
• Speed really matters

In those cases, use a set or dictionary instead!

Understanding Python List Memory Layout and Search Performance

Lists in Python are arrays of pointers. When Python performs a linear search, it:

1. Accesses contiguous memory locations in sequence
2. Benefits from CPU cache prefetching
3. Avoids jumping around to random memory addresses

This memory access pattern works well with modern CPU caches. For small-to-medium lists, the entire search might complete without a single cache miss.

Compare this to searching through a linked list or tree structure where each step requires following a pointer to a potentially random memory location. Linear search through an array wins decisively for small N, even if the theoretical complexity suggests otherwise.

Binary Search: The Smart Way to Search Sorted Data

Let me teach you a clever searching trick. Imagine you’re looking for a word in a dictionary.

You don’t start at “A” and check every single word until you find yours. That would take forever!

Instead, you open the dictionary somewhere in the middle. If your word comes before the middle page, you look in the left half. If it comes after, you look in the right half. Then you repeat this process.

Each time you look, you cut the remaining pages in half. That’s binary search!

How Binary Search Works Step by Step

Let’s see binary search in action with a simple example:

# We have a sorted list of numbers
numbers = [2, 5, 8, 12, 16, 23, 38, 45, 56, 67, 78]

# We're looking for 23

# Step 1: Check the middle (index 5)
# Middle value = 23
# Found it in just 1 step!

# Let's try looking for 67 to see more steps:

# Step 1: Check middle (index 5) → value is 23
#         67 > 23, so look in RIGHT half [38, 45, 56, 67, 78]

# Step 2: Check middle of right half (index 8) → value is 56
#         67 > 56, so look in RIGHT half [67, 78]

# Step 3: Check middle (index 9) → value is 67
#         Found it in 3 steps!

# With linear search, we would have checked 10 items
# With binary search, we only checked 3 items

Here’s the code that shows exactly how binary search works:

def binary_search_explained(sorted_list, target):
    """Binary search with detailed explanation of each step"""
    
    left = 0  # Start of the search range
    right = len(sorted_list) - 1  # End of the search range
    step = 0
    
    print(f"Looking for: {target}")
    print(f"In sorted list: {sorted_list}")
    print()
    
    while left <= right:
        step += 1
        middle = (left + right) // 2  # Find middle position
        middle_value = sorted_list[middle]
        
        print(f"Step {step}:")
        print(f"  Checking middle position {middle} → value is {middle_value}")
        
        if middle_value == target:
            print(f"  ✓ Found {target}!")
            print(f"\nTotal steps: {step}")
            print(f"Binary search is {len(sorted_list) - step} steps faster!")
            return middle
        
        elif middle_value < target:
            print(f"  {middle_value} < {target}, search RIGHT half")
            left = middle + 1
        
        else:
            print(f"  {middle_value} > {target}, search LEFT half")
            right = middle - 1
        
        print()
    
    print(f"✗ {target} not found")
    print(f"Total steps: {step}")
    return -1

# Try it yourself
numbers = [3, 7, 12, 18, 24, 29, 35, 41, 48, 55, 62, 70]
binary_search_explained(numbers, 41)

The output shows each step:

Looking for: 41
In sorted list: [3, 7, 12, 18, 24, 29, 35, 41, 48, 55, 62, 70]

Step 1:
  Checking middle position 5 → value is 29
  29 < 41, search RIGHT half

Step 2:
  Checking middle position 8 → value is 48
  48 > 41, search LEFT half

Step 3:
  Checking middle position 6 → value is 35
  35 < 41, search RIGHT half

Step 4:
  Checking middle position 7 → value is 41
  ✓ Found 41!

Total steps: 4
Binary search is 8 steps faster!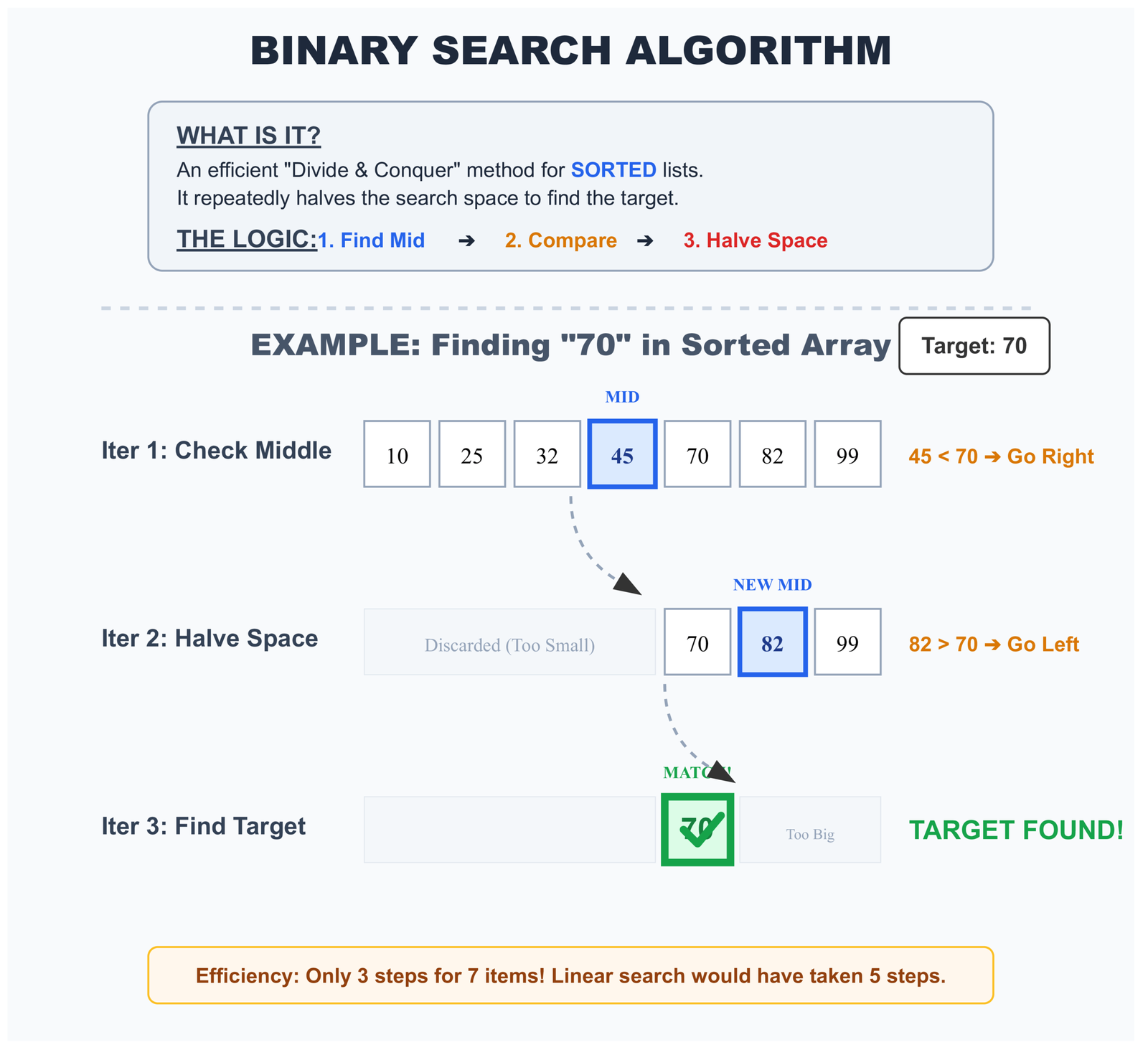

The One Rule You Must Follow: Your Data Must Be Sorted

Binary search only works if your data is sorted. This is super important!

# This works - data is sorted
sorted_numbers = [1, 5, 9, 13, 17, 21, 25]
# Binary search will work correctly

# This FAILS - data is NOT sorted
unsorted_numbers = [5, 1, 17, 9, 25, 13, 21]
# Binary search will give WRONG answers!

Why does binary search need sorted data? Because it makes decisions based on comparisons. When we check the middle and find 15, we decide "my target is bigger than 15, so it must be in the right half." But that only works if the data is sorted!

If your data isn't sorted, you have two choices:

1. Use linear search (check items one by one)
2. Sort your data first, then use binary search

For more advanced sorting techniques, check out our guide on sorting algorithms in Python.

Here's how the algorithm works:

def binary_search(sorted_list, target):
    left, right = 0, len(sorted_list) - 1
    comparisons = 0
    
    while left <= right:
        comparisons += 1
        mid = (left + right) // 2
        
        if sorted_list[mid] == target:
            return True, comparisons
        elif sorted_list[mid] < target:
            left = mid + 1  # Target must be in right half
        else:
            right = mid - 1  # Target must be in left half
    
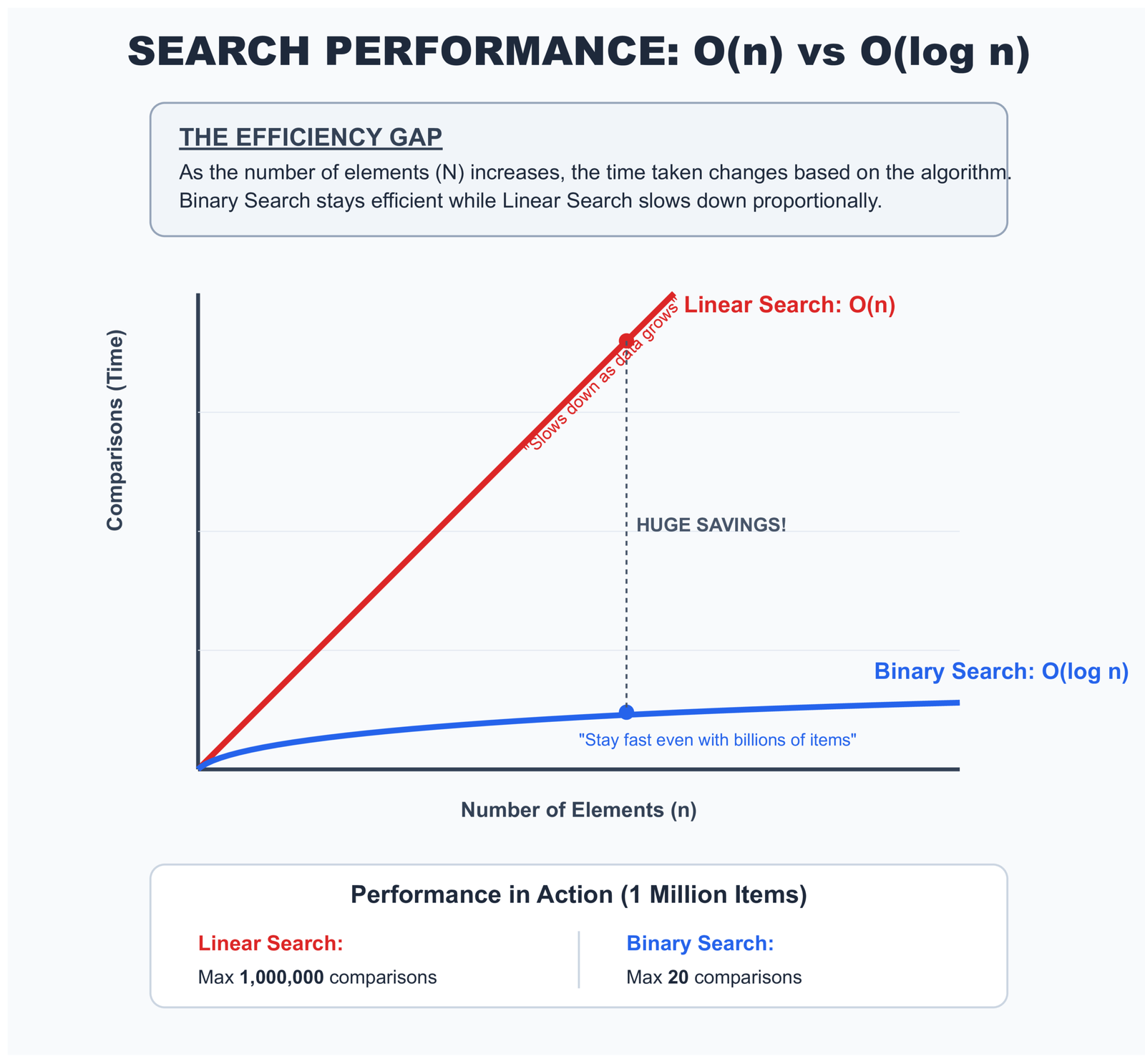
    return False, comparisons

For a sorted collection with N elements, binary search needs at most log₂(N) comparisons:

• 1,000 items: maximum 10 comparisons
• 1,000,000 items: maximum 20 comparisons
• 1,000,000,000 items: maximum 30 comparisons

Watch that pattern. As your data grows exponentially, the comparisons grow logarithmically. With large datasets, the difference between linear and binary search becomes the difference between "instant" and "unusable."

If you're working with sorting algorithms, understanding binary search becomes even more valuable since you can leverage sorted data for faster lookups.

Using Python's Bisect Module for Production-Ready Binary Search

Python won't apply binary search automatically. Even with perfectly sorted data, writing x in my_list still triggers a linear search.

You need to explicitly tell Python to use binary search through the bisect module:

import bisect

# Sorted list of user IDs
active_users = [101, 205, 347, 892, 1205, 2341, 5672]

# Linear search (slower) - Python's default
if user_id in active_users:
    grant_access()

# Binary search (faster) - explicit choice
index = bisect.bisect_left(active_users, user_id)
if index < len(active_users) and active_users[index] == user_id:
    grant_access()

The bisect module gives you these tools:

• bisect_left(): Finds where to insert an item, favoring the left position
• bisect_right(): Finds where to insert an item, favoring the right position
• insort_left(): Inserts an item while keeping the list sorted
• insort_right(): Inserts an item while keeping the list sorted

Understanding how functions work in Python helps you better utilize these bisect operations in your own code.

Should You Sort Your Data Before Searching? It Depends!

Here's a question many people ask: "If binary search is faster, should I always sort my data first?"

The answer: Not always! Sorting takes time too. Sometimes sorting costs more than it saves.

Understanding the Cost of Sorting

Let me show you with a real example:

# Imagine you have a list of 1000 numbers
numbers = [45, 12, 89, 33, 67, 23, ... ]  # 1000 unsorted numbers

# Option 1: Search without sorting (Linear Search)
# Cost: Check up to 1000 items = 1000 checks

if 67 in numbers:
    print("Found it!")

# Option 2: Sort first, then search (Binary Search)
# Cost: Sorting = about 10,000 operations
#       Then binary search = about 10 checks
# Total = 10,010 operations

sorted_numbers = sorted(numbers)  # This takes time!
# Then use binary search
# Total cost is HIGHER for just one search!

See the problem? For one search, sorting actually makes things slower!

When Sorting Makes Sense

Sorting becomes worth it when you search multiple times:

# Scenario: You need to search 100 times
numbers = [list of 1000 numbers]

# Option 1: Linear search 100 times
# Cost: 1000 checks × 100 searches = 100,000 checks total!

# Option 2: Sort once, then binary search 100 times
# Cost: 10,000 (sorting) + 10 (search) × 100 = 11,000 total
# This is MUCH faster!

# So for multiple searches:
sorted_numbers = sorted(numbers)  # Sort once

# Then search many times
for search_value in [67, 23, 89, 45, ... ]:  # 100 different searches
    if search_value in sorted_numbers:  # Each search is fast!
        print(f"Found {search_value}")

The Simple Decision Guide

Here's the code for each approach:

# Approach 1: One-time search - Just use linear search
user_ids = [101, 205, 309, 412, ...]
if 205 in user_ids:  # Simple and fine for one search
    print("User found")

# Approach 2: Multiple searches - Sort then binary search
import bisect

user_ids = sorted([101, 205, 309, 412, ...])  # Sort once

# Now search many times
for search_id in [205, 101, 412, 309]:
    index = bisect.bisect_left(user_ids, search_id)
    if index < len(user_ids) and user_ids[index] == search_id:
        print(f"User {search_id} found")

# Approach 3: Constant searching - Use a set
user_ids = {101, 205, 309, 412, ...}  # Create set once

# Search as many times as you want - always instant!
if 205 in user_ids:  # O(1) - Instant!
    print("User found")

Learning about Python optimization strategies will help you make these decisions more confidently in your own projects.

The decision matrix:

Scenario	Recommendation	Reason
One-time search	Linear search	Sorting cost exceeds search benefit
2-5 searches	Depends on N	Break-even point varies with data size
10+ searches	Sort then binary search	Amortized cost pays off
Continuous searches	Maintain sorted order	Use bisect.insort for insertions
Frequent modifications	Consider set/dict instead	Avoid repeated sorting overhead

Here's how to think about it:

# Wasteful: Sorting before every single search
def check_user_access(user_id, user_list):
    sorted_users = sorted(user_list)  # O(N log N) every time
    return user_id in sorted_users    # Then O(N) linear search!

# Better: Sort once, search many times
class UserDatabase:
    def __init__(self, user_list):
        self.users = sorted(user_list)  # Sort once during setup
    
    def has_user(self, user_id):
        index = bisect.bisect_left(self.users, user_id)
        return index < len(self.users) and self.users[index] == user_id

# Best: Use the right data structure from the start
class UserDatabase:
    def __init__(self, user_list):
        self.users = set(user_list)  # O(N) conversion once
    
    def has_user(self, user_id):
        return user_id in self.users  # O(1) lookup every time

If you're building applications that need to manage user data efficiently, learning about Python sets becomes essential for optimal performance.

Hash Lookup: The Instant Way to Find Things

Hash lookup is like having a magical index that tells you exactly where everything is. Let me explain with a real-world example.

Imagine you're a teacher with 30 students. You need to quickly find each student's grade.

Method 1 (List - Linear Search): You have a list of all students. To find Sarah's grade, you check: "Is this Sarah? No. Is this Sarah? No..." until you find her.

Method 2 (Dictionary - Hash Lookup): You have a grade book where each student's name is written on a tab. You just flip directly to the "S" section and find Sarah instantly!

That's the difference between a list and a dictionary. Dictionaries use "hash lookup" - they jump straight to the answer.

How Python Dictionaries Find Things Instantly

Let me show you with real code:

# Using a list (slower for searching)
student_grades_list = [
    ("Alice", 95),
    ("Bob", 87),
    ("Charlie", 92),
    ("Diana", 88),
    ("Eve", 90)
]

# To find Bob's grade, Python checks each student
for name, grade in student_grades_list:
    if name == "Bob":
        print(f"Bob's grade: {grade}")
        # Python had to check Alice, then Bob - 2 checks

# Using a dictionary (faster for searching)
student_grades_dict = {
    "Alice": 95,
    "Bob": 87,
    "Charlie": 92,
    "Diana": 88,
    "Eve": 90
}

# To find Bob's grade, Python jumps directly to it
print(f"Bob's grade: {student_grades_dict['Bob']}")
# Python jumped straight to Bob - 1 check!

# Or checking if a student exists
if "Bob" in student_grades_dict:
    print("Bob is in the class")
    # This is instant, regardless of how many students there are!

Understanding Hash Functions in Simple Terms

How does Python know where to jump? It uses something called a "hash function."

Think of a hash function like a formula that turns any name into a storage location number:

# Simplified example of how hashing works
# (Python's actual hash function is more complex)

def simple_hash(name):
    """Turn a name into a number"""
    total = 0
    for letter in name:
        total += ord(letter)  # Get number value of each letter
    return total

# Examples:
print(simple_hash("Bob"))     # Might give: 281
print(simple_hash("Alice"))   # Might give: 405
print(simple_hash("Charlie")) # Might give: 683

# Python uses these numbers to know exactly where to store
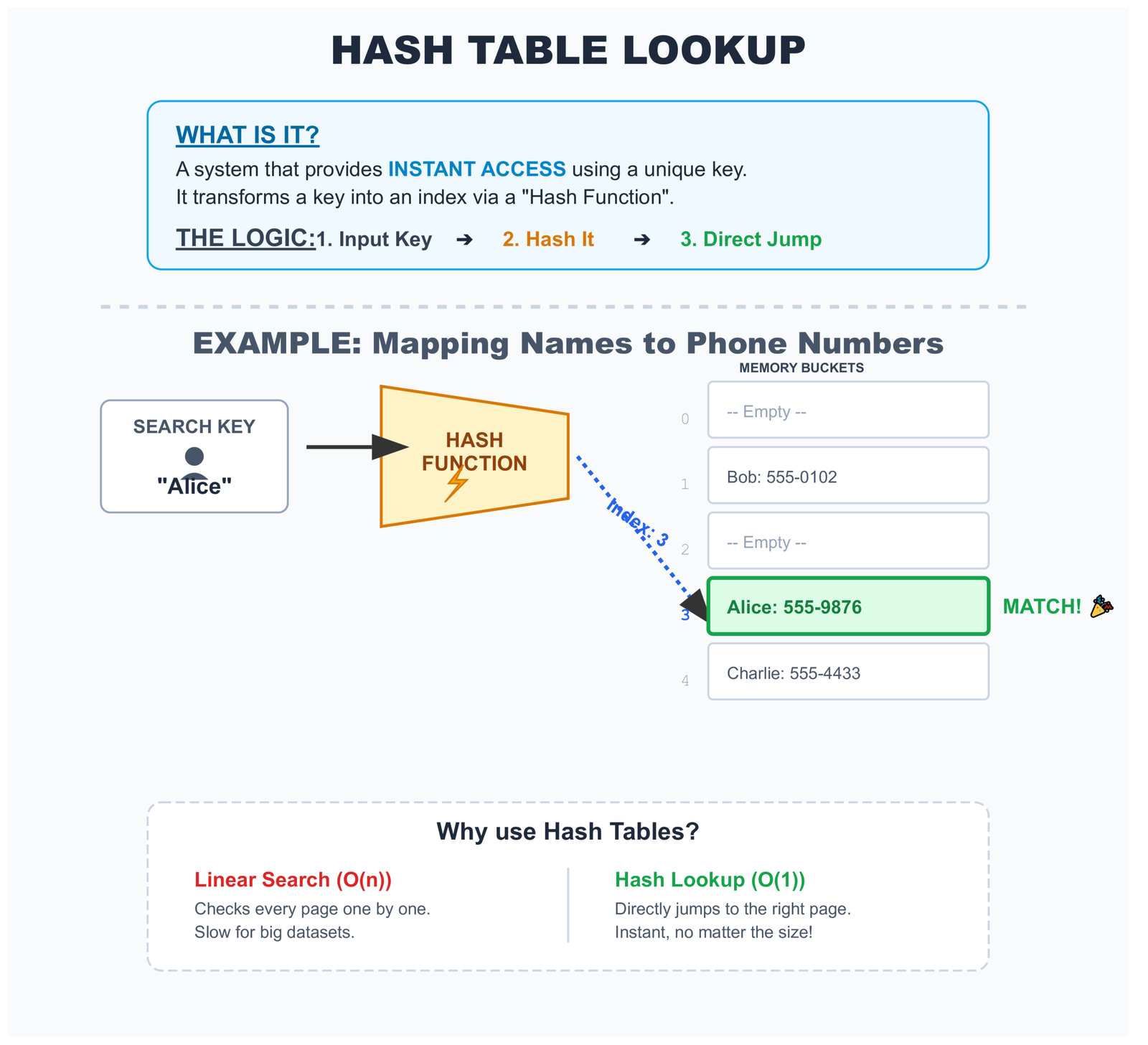
# and find each student's grade

When you ask for student_grades_dict["Bob"]:

1. Python calculates Bob's hash number (let's say 281)
2. Python jumps to storage location 281
3. Python finds Bob's grade right there - no searching needed!

Why Sets and Dictionaries Are So Fast

Both sets and dictionaries use hash lookup. That's why they're so fast for checking if something exists:

# Set example - checking if an email is on the blocklist
blocked_emails = {
    "spam1@bad.com",
    "spam2@bad.com", 
    "spam3@bad.com",
    # ... imagine 10,000 more emails
}

email = "test@good.com"

# This is instant, even with 10,000 blocked emails!
if email in blocked_emails:
    print("Email is blocked")
else:
    print("Email is allowed")

# Compare with a list:
blocked_emails_list = [
    "spam1@bad.com",
    "spam2@bad.com",
    "spam3@bad.com",
    # ... 10,000 more emails
]

# This might check thousands of emails one by one
if email in blocked_emails_list:
    print("Email is blocked")

The speed difference is huge:

• With a list of 10,000 emails: Python might check all 10,000 items
• With a set of 10,000 emails: Python checks 1 location and finds the answer

This is why experienced Python developers use sets and dictionaries for membership testing. If you're frequently checking "is this item in my collection?", always use a set or dictionary, not a list!

Understanding Hash Functions and Memory Addressing in Python

The process works in three quick steps:

1. Hash computation: Python calls hash(key) and gets back an integer
2. Index calculation: That hash value gets converted to a table index using modulo math
3. Direct access: Python reads that specific memory location immediately

# Simplified concept (not Python's actual implementation)
class SimpleHashTable:
    def __init__(self, size=8):
        self.size = size
        self.table = [None] * size
    
    def _hash(self, key):
        return hash(key) % self.size
    
    def __contains__(self, key):
        index = self._hash(key)
        bucket = self.table[index]
        
        if bucket is None:
            return False
        
        # Handle collisions: bucket might store multiple items
        for stored_key, value in bucket:
            if stored_key == key:
                return True
        return False

Most of the time, this completes in constant time O(1). The lookup speed stays the same whether your dictionary contains 10 items or 10 million items.

Why Python Sets and Dictionaries Outperform Lists for Membership Testing

The numbers speak clearly:

Operation	List	Set	Dict
Membership test (average)	O(N)	O(1)	O(1)
Membership test (worst)	O(N)	O(N)*	O(N)*
Add item	O(1)	O(1)	O(1)
Remove item	O(N)	O(1)	O(1)
Memory overhead	Low	High	High

* Worst case occurs with hash collisions, extremely rare in practice

Hash Collision Handling and Real-World Dictionary Performance Limitations

Hash tables aren't perfect. They trade memory for speed, and they rely on hash functions distributing keys evenly across the available space.

What Happens When Two Keys Hash to the Same Index

Hash collisions are mathematically inevitable. With limited table space and unlimited possible keys, some keys must occasionally map to the same position.

Python handles this using open addressing with random probing. When a collision happens:

1. Python calculates a secondary probe sequence
2. It checks the next location in that sequence
3. It continues until finding either an empty slot or your key

Theoretically, worst-case performance can degrade to O(N) if many keys collide repeatedly. But Python's hash function distributes keys so evenly that you'll rarely see this in practice.

Memory Overhead and When Dictionaries Become Inefficient

Every performance gain comes with a cost. For hash tables, that cost is memory.

Python dictionaries:

• Reserve extra space for future growth
• Keep their load factor below 66% to minimize collisions
• Store both keys and values (while sets only store keys)
• Use additional memory for hash table infrastructure

A dictionary holding 1,000 integers typically uses about 10 times more memory than a list holding those same integers.

import sys

numbers = list(range(1000))
numbers_set = set(range(1000))
numbers_dict = {i: i for i in range(1000)}

print(f"List: {sys.getsizeof(numbers)} bytes")
print(f"Set: {sys.getsizeof(numbers_set)} bytes")
print(f"Dict: {sys.getsizeof(numbers_dict)} bytes")

# Typical output:
# List: 9016 bytes
# Set: 32984 bytes
# Dict: 36968 bytes

When memory matters more than speed, lists win. When you're storing millions of items on limited hardware, that overhead adds up quickly.

Python Interpreter Optimizations That Affect Search Performance

Python includes optimizations that don't show up in pure algorithmic analysis but make a real difference in practice.

Why Built-in Membership Tests Beat Manual Loop Implementation

Writing your own search loop in Python runs slower than using the in operator, even when both perform identical operations.

import time

data = list(range(100000))
target = 99999

# Manual loop implementation
start = time.perf_counter()
found = False
for item in data:
    if item == target:
        found = True
        break
manual_time = time.perf_counter() - start

# Built-in operator
start = time.perf_counter()
found = target in data
builtin_time = time.perf_counter() - start

print(f"Manual loop: {manual_time:.6f}s")
print(f"Built-in: {builtin_time:.6f}s")
print(f"Speed improvement: {manual_time / builtin_time:.2f}x")

The built-in version runs faster because:

• It's implemented in C, not Python bytecode
• It bypasses Python's interpreter overhead on each iteration
• Memory access patterns get optimized at the C level
• It avoids creating Python objects during iteration

This matters for correctness, not just speed. Keep experimental code in practice files. Production code should use Python's built-in functionality whenever possible.

Understanding CPython Memory Layout and Cache Performance

Python lists store pointers to objects, not the actual objects themselves. This design choice has real implications for search performance:

• Good cache locality: The pointer array is contiguous and cache-friendly
• Indirection cost: Each comparison requires following a pointer to the actual object
• Type checking overhead: Python must verify types before performing comparisons

For small objects like integers or short strings, this overhead becomes noticeable. For larger objects like custom class instances or complex data structures, the indirection cost becomes negligible compared to the comparison operation itself.

Practical Decision Framework: Choosing the Right Search Strategy for Your Use Case

Forget algorithmic complexity for a moment. Real decisions require context.

Real-World Scenarios and Recommended Approaches

# Scenario 1: User authentication system
# Inefficient: List of valid usernames
valid_users = ['alice', 'bob', 'charlie', ...]
if username in valid_users:  # O(N) on every login attempt

# Efficient: Set of valid usernames
valid_users = {'alice', 'bob', 'charlie', ...}
if username in valid_users:  # O(1) on every login attempt


# Scenario 2: Rate limiting by IP address
# Inefficient: List of recent IPs with timestamps
recent_requests = [('192.168.1.1', time), ...]
for ip, timestamp in recent_requests:  # O(N) per request
    if ip == current_ip:
        check_rate_limit()

# Efficient: Dictionary mapping IP to timestamp
recent_requests = {'192.168.1.1': time, ...}
if current_ip in recent_requests:  # O(1) per request
    check_rate_limit()


# Scenario 3: Finding available seat numbers
# Inefficient: Unsorted list of taken seats
taken_seats = [15, 8, 23, 4, 42, ...]
if seat_number in taken_seats:  # O(N) check

# Efficient: Set of taken seats
taken_seats = {15, 8, 23, 4, 42, ...}
if seat_number in taken_seats:  # O(1) check


# Scenario 4: Product inventory with ordered search
# When you need both fast lookup and maintain order
from bisect import bisect_left, insort

class ProductInventory:
    def __init__(self):
        self.product_ids = []  # Kept sorted
    
    def add_product(self, product_id):
        insort(self.product_ids, product_id)  # Maintains sort order
    
    def has_product(self, product_id):
        i = bisect_left(self.product_ids, product_id)
        return i < len(self.product_ids) and self.product_ids[i] == product_id

For more complex data handling scenarios, you might want to explore working with different file formats or data analysis with pandas to handle larger datasets efficiently.

Common Python Search Performance Mistakes Developers Make Repeatedly

Some mistakes appear everywhere. Learning to spot them saves hours of debugging and prevents performance problems before they start.

Mistake 1: Using Binary Search on Unsorted Data Without Validation

# Silent correctness bug - no error, just wrong results
user_ids = [105, 203, 199, 501, 432]  # NOT sorted!

# This produces incorrect results without warning
from bisect import bisect_left
target = 199
index = bisect_left(user_ids, target)
found = index < len(user_ids) and user_ids[index] == target
print(found)  # Might print False even though 199 exists!

Binary search on unsorted data fails silently. Python won't raise an error. Your tests might miss it if they only check small datasets. If you're working with sorted data, always validate the sort order programmatically.

Mistake 2: Converting Between Data Structures Inside Hot Loops

# Performance disaster waiting to happen
def process_events(events, valid_event_ids):
    for event in events:
        # Converting to set on EVERY single iteration!
        if event.id in set(valid_event_ids):  # O(N) conversion repeated!
            handle_event(event)

# Correct approach - convert once
def process_events(events, valid_event_ids):
    valid_ids = set(valid_event_ids)  # O(N) once before loop
    for event in events:
        if event.id in valid_ids:  # O(1) per iteration
            handle_event(event)

Understanding how loops work in Python helps you avoid these expensive mistakes.

Mistake 3: Using Lists When Only Membership Testing Matters

# Inefficient choice - list when order doesn't matter
processed_user_ids = []
for user_id in incoming_requests:
    if user_id not in processed_user_ids:  # O(N) every check
        process_request(user_id)
        processed_user_ids.append(user_id)

# Efficient choice - set for membership tracking
processed_user_ids = set()
for user_id in incoming_requests:
    if user_id not in processed_user_ids:  # O(1) every check
        process_request(user_id)
        processed_user_ids.add(user_id)

If you only need to track "have I seen this before?", a set beats a list every time.

Mistake 4: Reimplementing Built-in Search in Application Code

# Don't write this in production code
def contains(items, target):
    for item in items:
        if item == target:
            return True
    return False

# Python already has this, optimized in C
result = target in items

Educational code belongs in learning environments. Production code should use battle-tested built-ins. If you're learning how to write functions, that's great for practice—just don't deploy it.

Mistake 5: Sorting Data Just to Use Binary Search Once

# Wasteful approach
user_list = get_users()  # Unsorted data
sorted_users = sorted(user_list)  # O(N log N) sorting cost
found = binary_search(sorted_users, target_user)  # O(log N) search
# Total cost: O(N log N) for one search

# Better approach
user_list = get_users()
found = target_user in user_list  # O(N) linear search
# Total cost: O(N) - actually faster!

Unless you're searching multiple times, sorting first costs more than it saves. Keep this in mind when optimizing your code.

Performance Measurement: Testing Search Performance in Real Python Code

Measure before optimizing. Intuition fails at scale.

import time
import random
from bisect import bisect_left

def benchmark_searches(size=100000, searches=1000):
    # Prepare data
    data_list = list(range(size))
    data_sorted = sorted(data_list)
    data_set = set(data_list)
    data_dict = {i: i for i in data_list}
    
    search_targets = [random.randint(0, size) for _ in range(searches)]
    
    # Benchmark linear search
    start = time.perf_counter()
    for target in search_targets:
        _ = target in data_list
    linear_time = time.perf_counter() - start
    
    # Benchmark binary search
    start = time.perf_counter()
    for target in search_targets:
        i = bisect_left(data_sorted, target)
        _ = i < len(data_sorted) and data_sorted[i] == target
    binary_time = time.perf_counter() - start
    
    # Benchmark set lookup
    start = time.perf_counter()
    for target in search_targets:
        _ = target in data_set
    set_time = time.perf_counter() - start
    
    # Benchmark dict lookup
    start = time.perf_counter()
    for target in search_targets:
        _ = target in data_dict
    dict_time = time.perf_counter() - start
    
    print(f"Results for {searches} searches in {size} items:")
    print(f"Linear search: {linear_time:.4f}s")
    print(f"Binary search: {binary_time:.4f}s")
    print(f"Set lookup: {set_time:.4f}s")
    print(f"Dict lookup: {dict_time:.4f}s")
    print(f"\nSpeed-up (set vs linear): {linear_time / set_time:.0f}x")

benchmark_searches()

The Fundamental Truth About Python Search Performance Most Tutorials Miss

Search algorithms don't exist in isolation. They're consequences of the data structure choices you made earlier.

Python doesn't decide how to search your data. You decided the moment you typed list, set, or dict.

That single choice propagates through everything that follows. Every membership test. Every lookup. Every existence check.

Data Structures Determine Algorithm Behavior in Python

Look at this sequence:

# This line determines everything that comes after
users = []  # vs. users = set() vs. users = {}

# Performance was already decided three lines ago
if current_user in users:
    grant_access()

The algorithm Python uses depends on that first line. Not on what's stored in the collection. Not on how many items exist. Just on the type you chose.

Real optimization isn't about writing clever code. It's about choosing appropriate data structures from the beginning. Understanding Python classes and objects helps you make better structural decisions in your code.

Why Python Leaves Search Strategy Decisions to Developers

Some languages try to optimize automatically. Python deliberately doesn't.

Python could theoretically detect repeated membership tests on a list and convert it to a set internally. It doesn't, and here's why:

• Lists maintain insertion order; sets don't care about order
• Lists allow duplicate values; sets automatically remove duplicates
• Lists use less memory; sets trade memory for lookup speed
• Converting has its own cost that might exceed any benefit

Python trusts you to understand your needs. It provides the tools. You decide when and how to use them. Learning about mutable versus immutable types helps you make these decisions more effectively.

What You Should Do Now: Practical Steps to Use This Knowledge

You've learned about three different ways Python searches data. Now let's put this knowledge to work in your own programs!

Step 1: Check Your Existing Code

Look at your programs and find places where you write if x in my_collection:

Ask yourself these questions:

• How many items are in my collection? (If less than 100, you're fine with a list)
• How often do I search? (If many times, consider a set or dict)
• Is my data sorted? (If yes, you could use binary search)

Step 2: Make Simple Improvements

Here are the most common improvements you can make right now:

# BEFORE: Using a list for frequent membership checks
blocked_users = ["user1", "user2", "user3", ...]

if current_user in blocked_users:  # Slow with many users
    deny_access()

# AFTER: Using a set for frequent membership checks
blocked_users = {"user1", "user2", "user3", ...}

if current_user in blocked_users:  # Fast! Always instant
    deny_access()

# BEFORE: Searching through a list many times
product_ids = [101, 205, 309, 412, ...]

for order_id in customer_orders:  # Searches list each time
    if order_id in product_ids:
        process_order(order_id)

# AFTER: Convert to set once, search many times
product_ids = {101, 205, 309, 412, ...}

for order_id in customer_orders:  # Instant lookup each time!
    if order_id in product_ids:
        process_order(order_id)

Step 3: Learn When to Use Each Method

Step 4: Keep Learning

Understanding search methods is just the beginning. Here are related topics that will help you write better Python code:

• Writing better functions to organize your search code
• Error handling for when items aren't found
• Classes and objects for building more complex data structures
• Data analysis with Pandas for working with large datasets

The Most Important Thing to Remember

The data structure you choose determines how Python searches. It's not about making your search algorithm faster - it's about picking the right tool from the start.

Think of it like this:

• Need to check membership often? → Use a set
• Need to look up values by key? → Use a dict
• Need to keep things in order? → Use a list
• Have sorted data and search often? → Use list + bisect

That's it! Start applying these ideas in your code today. Your programs will run faster, and you'll understand exactly why.

Frequently Asked Questions About Python Search Algorithms

External Resources for Further Learning

Test Your Knowledge: Python Search Algorithms Quiz