How to Build a Neural Network from scratch using Python
Introduction
In this, we will take a closer look at Neural network, a key part of machine learning and artificial intelligence (AI). Neural networks help computers learn from data and make smart decisions. They are used in many areas, from recognizing faces in photos to translating languages.
Our goal here is simple: to guide you through building a neural network from scratch using Python. We’ll start from the basics and work our way up, making it easy to understand. By the end of this post, you’ll know how to code your own neural network in Python.
Understanding Neural Network
What is a Neural Network?
Imagine your brain is like a big, complex network of tiny computers, each called a “neuron.” These neurons work together to understand things and make decisions.
A neural network in computers works like this. It’s a system made up of many small units called “nodes” that are connected in layers. Each node takes in some information, does a little bit of work with it, and then passes it along to the next layer of nodes.
Just like your brain learns from experience and gets better at recognizing patterns or making decisions, a neural network learns from data. It uses this learning to make predictions or decisions based on the information it has processed.
In short, a neural network is a simple version of how our brains work, using nodes to learn from data and make decisions.
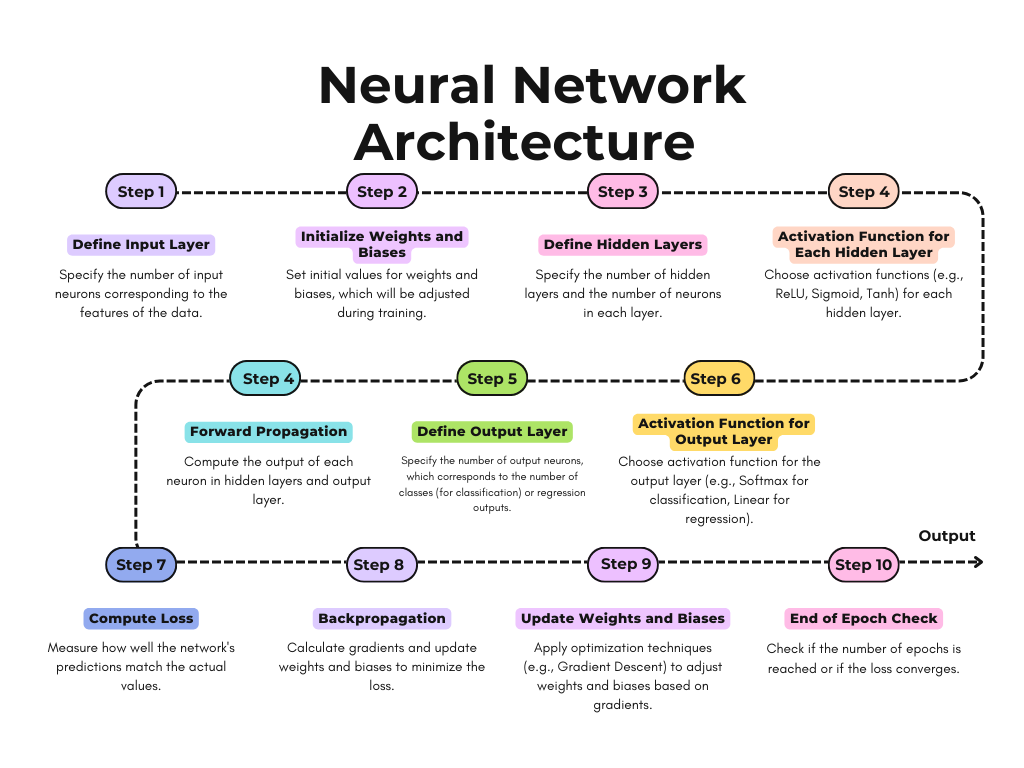
Explanation of Neural Network Architecture
In a neural network, the information moves through several layers. Each layer does its job and passes the results along to the next layer, kind of like a relay race where the baton (or information) keeps moving forward until the final result is achieved.
- Neurons: These are the basic units of a neural network, similar to how nerve cells work in our brain. Each neuron receives input, processes it, and passes the result to the next layer.
- Layers: Neural networks are made up of layers:
- Input Layer: This is where data enters the network.
- Hidden Layers: These are the layers between the input and output. They help the network learn complex patterns.
- Output Layer: This layer produces the final result or prediction.
- Weights: Think of the connections between neurons like roads in a city. Each road has a different width, which represents how important it is for getting traffic from one place to another. In a neural network, these “roads” are called weights. When the network is learning, it changes the width of these roads to make sure information travels more effectively. By adjusting these weights, the network gets better at making accurate predictions.
Understanding the architecture of a neural network helps explain how it processes and learns from data.
Types of Neural Networks
Neural networks come in various types, each designed for different tasks. Here are some of the most common ones:
Feedforward Neural Networks
Feedforward Neural Networks are like a simple conveyor belt system. Imagine you have a series of steps where something moves from start to finish in one smooth path.
- Input Layer: This is where the information enters the system. Think of it as the starting point of the conveyor belt.
- Hidden Layers: After the information enters the input layer, it moves through one or more intermediate layers called hidden layers. These layers process the information and help figure out patterns.
- Output Layer: Finally, the information reaches the output layer, where the network makes its final decision or prediction.
In a Feedforward Neural Network, this movement is always in one direction—from the input layer, through the hidden layers, and to the output layer. There’s no looping back or revisiting previous layers.
This straightforward design makes Feedforward Neural Networks useful for basic tasks like sorting data into categories (classification) or predicting values based on input (regression).
Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs) are like specialized tools designed for working with images and visual data. Here’s how they work and why they’re so effective:
- Visual Data Processing: These are built to handle images, which are complex because they have different patterns and features. Imagine trying to recognize a face in a crowd or detect a cat in a photo—this is where CNNs shine.
- Pattern Recognition: CNNs are particularly good at spotting patterns in images. They can identify specific features like edges, shapes, and textures, which are essential for recognizing objects or faces.
- Special Layers: Convolutional Neural Networks use unique layers called convolutional layers to do this pattern recognition. These layers act like a series of small windows that slide over the image. Each window looks at a small portion of the image at a time, detecting different features like edges or corners. By combining information from these windows, CNNs build up a detailed understanding of what’s in the image.
- Spatial Hierarchies: CNNs also use layers called pooling layers that help reduce the amount of detail while keeping important features. This process helps the network focus on the most critical aspects of the image without being overwhelmed by too much detail.
- Deep Understanding: As information passes through multiple convolutional and pooling layers, CNNs learn increasingly complex features. For instance, the first layers might detect simple shapes, while deeper layers might recognize more complex objects like faces or animals.
Overall, CNNs are excellent at analyzing visual data because they’re designed to understand and interpret patterns in images, making them perfect for tasks like object recognition or facial recognition.
Recurrent Neural Networks (RNNs)
Recurrent Neural Networks (RNNs) are like memory-equipped tools designed for handling sequences of information, such as time series data or text. Here’s how they work and why they’re useful:
- Handling Sequences: These are built to work with data that comes in a sequence, like a series of words in a sentence or measurements over time. Unlike some other neural networks, RNNs can keep track of the order and context of this sequential data.
- Memory of Previous Inputs: Imagine you’re reading a sentence. To understand the meaning of a word, you need to remember the words that came before it. RNNs have a special ability to remember previous inputs, which helps them make more accurate predictions. This is because they have connections that loop back, allowing information to be carried from one step in the sequence to the next.
- Making Predictions: This memory feature lets RNNs use past information to improve their predictions. For example, in language translation, knowing the context of previous words helps the RNN predict the next word more accurately. In speech recognition, remembering previous sounds helps in understanding and transcribing spoken words.
- Applications: RNNs are great for tasks that involve sequences. They are used in:
- Language Translation: RNNs can translate text from one language to another by understanding the sequence and context of words.
- Speech Recognition: They can convert spoken words into written text by analyzing the sequence of sounds and their context.
- Time Series Analysis: RNNs can analyze patterns in data collected over time, such as stock prices or weather data.
By understanding these types of neural networks, you can choose the right one for your specific problem and improve your machine learning projects.
Key Concepts in Neural Network
Activation Functions
These are like the decision-makers in a neural network. They help determine how a neuron should react to the input it receives. Here’s a detailed look at what they do and some common types:
What Activation Functions Do:
Role: Activation functions decide whether a neuron should be “activated” or not. This means they help decide if the neuron should “fire” (send a signal to the next layer) based on the input it gets.
Purpose: Without activation functions, the network would just be a series of linear equations, and it wouldn’t be able to learn complex patterns. Activation functions add non-linearity to the network, allowing it to learn and model more complex relationships.
Common Activation Functions:
Sigmoid Function:
How It Works: This function squashes the output of the neuron to be between 0 and 1. Think of it like compressing a range of numbers into a narrow band.
When to Use: It’s commonly used in problems where you need to classify something into one of two categories. For example, if you want to determine whether an image contains a cat or not, the sigmoid function will give you a probability between 0 and 1. A value close to 0 means “no cat,” while a value close to 1 means “cat.”
ReLU (Rectified Linear Unit):
How It Works: ReLU outputs the input directly if it’s positive. If the input is negative, it outputs zero. It’s like having a gate that only lets positive values through and blocks negatives.
When to Use: ReLU is popular because it speeds up learning and helps avoid issues like vanishing gradients, which can slow down training. It’s often used in tasks like image recognition, where you need the network to detect various features in images.
Tanh (Hyperbolic Tangent):
How It Works: Tanh scales the output to be between -1 and 1. It’s like having a function that stretches and squashes values so they’re centered around zero.
When to Use: Tanh is useful when you need the output to reflect both positive and negative patterns. For example, in cases where the network needs to understand varying intensities or directions, tanh can be a good choice.
Why Understanding Activation Functions Matters:
Choosing the Right One: Knowing how each activation function works helps you pick the right one for your neural network. The right choice can make your network learn more effectively and perform better on tasks.
In summary, activation functions are essential because they help the network make decisions about which signals to pass on and how to process them. By understanding these functions, you can design better neural networks that are capable of solving complex problems.
Loss Functions
These are like report cards for your neural network. They tell you how well your network is doing by comparing its predictions to the actual results. Here’s a detailed look at what loss functions are and how they work:
What Loss Functions Do
Purpose: Loss functions measure the difference between what the network predicted and what the actual result was. This difference is called an “error,” and the loss function calculates how big that error is.
Feedback: By calculating this error, loss functions provide feedback to the network. This feedback helps the network learn and improve by adjusting its weights and biases to reduce the error.
Common Loss Functions
Mean Squared Error (MSE)
How It Works: MSE calculates the average of the squared differences between the predicted values and the actual values. Squaring the differences makes larger errors more significant.
When to Use: It’s commonly used in tasks where you need to predict continuous values. For example, if you’re predicting house prices based on various features (like size and location), MSE helps measure how close your predicted prices are to the actual prices.
Cross-Entropy
How It Works: Cross-Entropy measures how well the network’s predicted probabilities match the actual categories. It’s particularly useful for classification tasks, where the network predicts a probability for each category (like whether an image contains a dog or a cat).
When to Use: It’s used when you have a classification problem with probabilities as outputs. For instance, if your network needs to decide whether an image is a dog or a cat, cross-entropy helps improve the network’s ability to make accurate classifications.
Why Loss Functions Are Important:
Guiding Training: Loss functions are crucial because they guide the training process. By showing how far off the network’s predictions are from the actual results, they help the network learn and adjust its parameters.
Improving Accuracy: With the feedback from the loss function, the network can adjust its settings to reduce errors and improve its accuracy over time.
In summary, loss functions are essential tools that measure how well a neural network is performing. They help guide the training process by showing how close or far off the network’s predictions are from the true values, enabling the network to make adjustments and improve its accuracy.
Backpropagation
Backpropagation is like the learning process for a neural network, helping it improve by correcting its mistakes. Here’s a step-by-step explanation of how it works:
Forward Pass
What Happens: The network starts by making a prediction. It does this by passing the input data through its layers—like sending a message through a series of filters.
Example: Imagine you’re trying to guess the price of a house based on its features (size, location, etc.). The network makes a guess about the price.
Calculate Loss
What Happens: Once the network has made a prediction, the loss function calculates how far off the prediction is from the actual result. This “error” shows how wrong the network was.
Example: If the actual price of the house is $300,000 and the network guessed $280,000, the loss function calculates the difference between these two numbers.
Backward Pass
What Happens: Backpropagation starts now. It calculates how much each weight (connection strength between neurons) contributed to the error. This is done by finding the gradient of the loss function with respect to each weight.
How It Works: Imagine each weight is like a dial on a machine. Backpropagation figures out how turning each dial would affect the overall error.
Update Weights
What Happens: Using the information from the backward pass, the network adjusts the weights. The goal is to adjust these weights so that future predictions are more accurate.
Example: If the network learned that increasing certain features (like house size) should lead to a higher price prediction, it adjusts the weights related to those features accordingly.
Learning Process
What It Achieves: By repeatedly using backpropagation, the network continuously adjusts its weights based on the errors it makes. Over time, this helps the network make better predictions because it learns from its mistakes and improves its accuracy.
In summary, backpropagation is the key process that helps neural networks learn. It involves making predictions, calculating errors, and then adjusting the connections between neurons to reduce those errors. This process makes the network better at making accurate predictions as it trains.
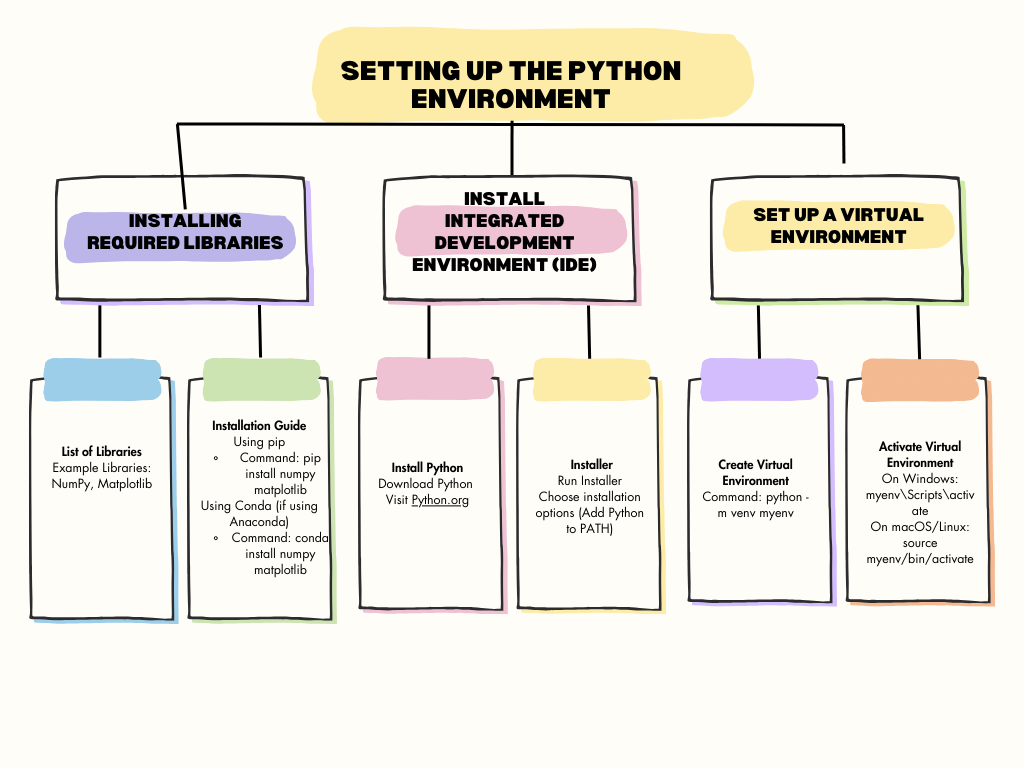
Setting Up Your Development Environment
To code efficiently, it’s important to set up a good development environment. Here’s a detailed step-by-step guide to get everything ready:
1. Install Python
- What to Do: Download and install the latest version of Python from the official Python website.
- Important Step: During installation, make sure to check the box that says “Add Python to PATH.” This allows you to use Python from the command line or terminal.
2. Choose an IDE or Code Editor
An Integrated Development Environment (IDE) or a code editor helps you write and manage your code more easily. Here are two popular options:
- Visual Studio Code (VS Code):
- What It Is: A free, versatile code editor that supports many programming languages and has a lot of extensions for Python.
- How to Get It: Download and install Visual Studio Code from the official website.
- PyCharm:
- What It Is: A dedicated Python IDE with many built-in features for coding, debugging, and managing Python projects.
- How to Get It: Download and install PyCharm from the official website.
3. Set Up a Virtual Environment
A virtual environment helps you manage the specific packages and libraries your project needs, without affecting your system-wide Python installation. Here’s how to set it up:
- Open Your Command Line or Terminal: This is where you’ll type the commands to create and manage your virtual environment.
- Navigate to Your Project Folder: Use the
cdcommand to move to the directory where you want to keep your project. - Create a Virtual Environment:
python -m venv myenv
This command creates a new virtual environment named myenv.
Activate the Virtual Environment:
- Windows
myenv\Scripts\activate
- Mac/Linux
source myenv/bin/activate
Activating the virtual environment changes your command line prompt to show that you’re now working inside the myenv environment.
4. Installing Required Libraries
Python libraries are packages of pre-written code that make it easier to perform specific tasks, such as handling data or building neural networks. Here’s a list of key libraries you’ll need and how to install them:
NumPy
- What It Is: NumPy is a library used for numerical operations. It’s great for working with arrays and performing mathematical computations, which are fundamental in neural networks.
- Why You Need It: Neural networks require a lot of mathematical operations, and NumPy helps manage these efficiently.
- How to Install: Open your command line or terminal and type the following command:
pip install numpy
Matplotlib
- What It Is: Matplotlib is a library for creating visualizations like plots and graphs. It helps you visualize your data and understand how your neural network is performing.
- Why You Need It: Visualizations are crucial for analyzing data and monitoring the progress of your neural network training.
- How to Install: In the command line or terminal, type the following command:
pip install matplotlib
TensorFlow or PyTorch
What They Are: TensorFlow and PyTorch are powerful libraries specifically designed for building and training neural networks. They provide tools and functions to create and optimize neural network models.
Why You Need Them: These libraries are essential for implementing neural networks. You can choose either based on your preference or the requirements of your project.
TensorFlow Installation: TensorFlow is developed by Google and is widely used in the industry. To install it, type the following command:
pip install tensorflow
PyTorch Installation: PyTorch is developed by Facebook and is popular for research and academic use. Visit the PyTorch website to get installation commands tailored to your operating system. The site will provide the specific command based on your environment and preferences.
By installing these libraries, you’ll set up a perfect environment for building and working with neural networks.
5. Verify the Setup
To make sure everything is set up correctly, you can run a simple Python script to check if the libraries are installed:
- Create a New Python File: Open your IDE or code editor and create a new Python file, such as
test_setup.py. - Add the Following Code
import numpy as np
import matplotlib.pyplot as plt
print("Setup is complete!")
- Run the Script: Save the file and run it from your command line or terminal with:
python test_setup.py
If everything is installed correctly, you should see the message “Setup is complete!” in the output.
By following these steps, you’ll set up a well-organized Python environment ready for coding and working with neural networks.
Building a Neural Network from Scratch
Building a neural network from scratch involves several steps. Here’s a detailed guide to help you understand and implement each step using Python code.
Step 1: Initializing the Network
Before you train your neural network, you need to set up its basic components, which include weights and biases. These components are crucial because they determine how data flows through the network and how it learns.
1. What Are Weights and Biases?
- Weights: These are the parameters that determine the strength of the connection between neurons in different layers. In simple terms, they decide how much influence one neuron has on another.
- Biases: These are additional parameters added to the output of neurons. They help the network make better predictions by shifting the activation function.
2. Why Initialize Weights and Biases?
- Initialization: At the start, weights are usually set to random values, and biases are often set to zero. This is because you need a starting point to begin the learning process. During training, these weights will be adjusted based on the errors made by the network.
3. Code Example
Here’s how you can initialize a simple neural network using Python and NumPy:
import numpy as np
# Initialize weights and biases
def initialize_network(input_size, hidden_size, output_size):
# Randomly initialize weights for the connections between the input and hidden layers
weights_input_hidden = np.random.randn(input_size, hidden_size)
# Initialize biases for the hidden layer to zeros
biases_hidden = np.zeros((1, hidden_size))
# Randomly initialize weights for the connections between the hidden and output layers
weights_hidden_output = np.random.randn(hidden_size, output_size)
# Initialize biases for the output layer to zeros
biases_output = np.zeros((1, output_size))
return weights_input_hidden, biases_hidden, weights_hidden_output, biases_output
# Example sizes for the layers
input_size = 3 # Number of features in the input data
hidden_size = 5 # Number of neurons in the hidden layer
output_size = 2 # Number of neurons in the output layer (e.g., classes or predictions)
# Initialize the network with the given sizes
weights_input_hidden, biases_hidden, weights_hidden_output, biases_output = initialize_network(input_size, hidden_size, output_size)
4. Explanation of the Code
- Import NumPy: We use NumPy, a powerful library for numerical operations, to handle arrays and random number generation.
- Define the
initialize_networkFunction:weights_input_hidden: Initializes the weights connecting the input layer to the hidden layer. Random values are used here to start the learning process.biases_hidden: Initializes biases for the hidden layer to zeros.weights_hidden_output: Initializes the weights connecting the hidden layer to the output layer with random values.biases_output: Initializes biases for the output layer to zeros.
- Specify Sizes:
input_size: The number of features or input variables.hidden_size: The number of neurons in the hidden layer (you can choose this based on your problem).output_size: The number of output neurons (e.g., the number of classes for classification).
- Initialize the Network: Call the
initialize_networkfunction with the sizes of your layers to get the weights and biases ready for training.
In this first step, you set up the neural network by initializing the weights and biases. This initial setup is important because it provides the starting point for the network to begin learning from the data. As training progresses, these weights and biases will be adjusted to improve the network’s performance.
Must Read
- How to Check if Dictionary Values Are Sorted in Python
- Check If a Tuple Is Sorted in Python — 5 Methods Explained
- How to Check If a List Is Sorted in Python (Without Using sort()) – 5 Efficient Methods
- How Python Searches Data: Linear Search, Binary Search, and Hash Lookup Explained
- I Implemented Every Sorting Algorithm in Python — The Results Nobody Talks About (Benchmarked on CPython)
Step 2: Forward Propagation
Forward propagation is a crucial part of how a neural network makes predictions. It involves sending input data through the network and computing the output.
How Forward Propagation Works
- Input Layer:
- Role: The input layer is where the raw data enters the neural network.
- Process: Each feature of the input data is multiplied by its corresponding weight. These weights determine the importance of each feature for the network’s prediction.
- Hidden Layers:
- Role: The hidden layers are where the main processing happens. They are called “hidden” because they are not directly visible in the input or output.
- Process: The weighted inputs from the input layer are processed through one or more hidden layers. Each neuron in these layers applies an activation function to decide how much it should “fire” or activate. This helps the network learn complex patterns.
- Output Layer:
- Role: The output layer generates the final prediction of the network.
- Process: The processed information from the hidden layers is passed to the output layer, which applies its own activation function to produce the final result.
Code Example
Here’s a simple Python code example to illustrate forward propagation:
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def forward_propagation(X, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output):
# Calculate inputs to hidden layer
hidden_layer_input = np.dot(X, weights_input_hidden) + biases_hidden
# Apply activation function to hidden layer
hidden_layer_output = sigmoid(hidden_layer_input)
# Calculate inputs to output layer
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output) + biases_output
# Apply activation function to output layer
output_layer_output = sigmoid(output_layer_input)
return output_layer_output
# Example input data
X = np.array([[0.1, 0.2, 0.3]])
output = forward_propagation(X, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
Explanation of the Code
- Sigmoid Function:
- What It Does: The
sigmoidfunction transforms its input into a value between 0 and 1. This is useful for creating probabilities or deciding whether a neuron should be activated. - Why It’s Important: It adds non-linearity to the network, which allows it to learn complex patterns. Without this function, the network would only be able to learn linear relationships.
- What It Does: The
- Forward Propagation Function:
- Inputs:
X: The input data to the network.weights_input_hidden,biases_hidden,weights_hidden_output,biases_output: The weights and biases for the connections between the layers.
- Process:
- Hidden Layer Input: Compute by multiplying the input data
Xby the weights connecting the input layer to the hidden layer and adding the biases for the hidden layer. - Hidden Layer Output: Apply the
sigmoidfunction to the hidden layer input to get the activated output of the hidden layer. - Output Layer Input: Compute by multiplying the hidden layer output by the weights connecting the hidden layer to the output layer and adding the biases for the output layer.
- Output Layer Output: Apply the
sigmoidfunction to this input to get the final output of the network.
- Hidden Layer Input: Compute by multiplying the input data
- Inputs:
- Result:
- What It Represents: The
output_layer_outputgives you the network’s prediction based on the input data. In this case, the output will be between 0 and 1, representing the network’s confidence in its prediction.
- What It Represents: The
Step 3: Computing the Loss
Computing the loss is a crucial step in training a neural network. It helps you measure how far off your network’s predictions are from the actual results. The goal is to minimize this loss, which means improving the accuracy of the network’s predictions.
What is the Loss Function?
- Purpose: The loss function quantifies the difference between the predicted outputs of the network and the actual labels. A smaller loss value indicates that the predictions are closer to the true values, while a larger loss indicates more errors.
- How It Works: It calculates the error between the predicted values (
y_pred) and the actual values (y_true). The network uses this error to make adjustments during training to improve its predictions.
Why Use the Cross-Entropy Loss Function?
For classification tasks, where the network needs to classify input data into categories (like identifying whether an image is of a cat or dog), the cross-entropy loss function is commonly used.
- Cross-Entropy Loss: This loss function measures how well the predicted probabilities match the true class labels. It is particularly effective when dealing with probabilities, which is common in classification problems.
Code Example
Here’s an example of Python code for calculating cross-entropy loss:
import numpy as np
def compute_loss(y_true, y_pred):
m = y_true.shape[0] # Number of samples
# Cross-entropy loss formula
loss = -np.sum(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)) / m
return loss
# Example true labels and predictions
y_true = np.array([[1, 0]]) # True labels
y_pred = np.array([[0.8, 0.2]]) # Predicted probabilities
# Compute the loss
loss = compute_loss(y_true, y_pred)
print("Loss:", loss)
Explanation of the Code
- Function Definition:
compute_loss(y_true, y_pred)- Inputs:
y_true: The true labels for the samples. For binary classification, these are typically 0 or 1.y_pred: The predicted probabilities from the network. These values are between 0 and 1, representing the network’s confidence in its predictions.
- Steps:
- Calculate Number of Samples:
m = y_true.shape[0]gives the number of samples in the batch. - Compute Loss:
- Formula:
-np.sum(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)) / my_true * np.log(y_pred): This term calculates the loss for the correctly predicted classes.(1 - y_true) * np.log(1 - y_pred): This term calculates the loss for the incorrectly predicted classes.-np.sum(...): Summing the results and taking the negative to get the loss value./ m: Averaging the loss over all samples.
- Formula:
- Calculate Number of Samples:
- Inputs:
- Example Usage:
- True Labels:
y_true = np.array([[1, 0]])indicates that the actual label for the sample is class 1. - Predicted Probabilities:
y_pred = np.array([[0.8, 0.2]])shows that the network predicted a probability of 0.8 for class 1 and 0.2 for class 0. - Compute Loss: The function calculates how well these predicted probabilities match the true labels.
- True Labels:
Computing the loss is an important step in training a neural network. By using the cross-entropy loss function, you can measure how well the network’s predictions align with the actual class labels. This measurement guides the network in adjusting its weights during training to improve its accuracy
Step 4: Backpropagation
Backpropagation is a key step in training neural networks. It helps the network learn by adjusting the weights and biases based on the errors made during prediction. Here’s how it works, explained in a simple way:
Code Example
Here’s a Python code example that demonstrates backpropagation:
import numpy as np
def sigmoid_derivative(x):
# Derivative of the sigmoid function
return x * (1 - x)
def backpropagation(X, y_true, y_pred, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output):
m = y_true.shape[0] # Number of samples
# Calculate error at output layer
output_error = y_pred - y_true
# Calculate delta for output layer (how much to adjust the weights)
output_delta = output_error * sigmoid_derivative(y_pred)
# Calculate hidden layer output
hidden_layer_output = sigmoid(np.dot(X, weights_input_hidden) + biases_hidden)
# Calculate error at hidden layer
hidden_error = np.dot(output_delta, weights_hidden_output.T)
# Calculate delta for hidden layer
hidden_delta = hidden_error * sigmoid_derivative(hidden_layer_output)
return output_delta, hidden_delta
# Example true labels and predictions
y_true = np.array([[1, 0]])
X = np.array([[0.1, 0.2, 0.3]])
weights_input_hidden = np.random.randn(3, 5)
biases_hidden = np.zeros((1, 5))
weights_hidden_output = np.random.randn(5, 2)
biases_output = np.zeros((1, 2))
# Forward pass to get predictions (example)
output = sigmoid(np.dot(X, weights_input_hidden) + biases_hidden)
output = sigmoid(np.dot(output, weights_hidden_output) + biases_output)
# Compute deltas
output_delta, hidden_delta = backpropagation(X, y_true, output, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
Explanation of the Code
- Sigmoid Derivative Function:
sigmoid_derivative(x)calculates how the sigmoid function’s output changes. This is important for determining how much each weight contributed to the error. - Backpropagation Function:
- Inputs:
X: Input data.y_true: True labels.y_pred: Predicted outputs from the network.weights_input_hidden,biases_hidden,weights_hidden_output,biases_output: Parameters of the network.
- Calculate Output Error:
output_error = y_pred - y_truegives the difference between the predicted and actual values at the output layer. - Calculate Output Delta:
output_delta = output_error * sigmoid_derivative(y_pred)adjusts the weights in the output layer based on the error and the sigmoid function’s derivative. - Hidden Layer Error:
hidden_error = np.dot(output_delta, weights_hidden_output.T)calculates the error propagated back to the hidden layer. - Calculate Hidden Delta:
hidden_delta = hidden_error * sigmoid_derivative(hidden_layer_output)adjusts the weights in the hidden layer.
- Inputs:
- Using the Code:
- Forward Pass: To get
output, the input dataXis passed through the network layers. - Compute Deltas: The
backpropagationfunction calculates how much to adjust each weight based on the error and the derivative of the activation functions.
- Forward Pass: To get
Backpropagation is essential for training neural networks as it adjusts the weights and biases to minimize errors. By calculating how much each weight and bias should change based on the errors made, the network improves its predictions over time.
Step 5: Updating Weights
After calculating how much each weight and bias in the neural network should change during backpropagation, the next step is to update these parameters. This process is essential for improving the network’s performance. Here’s a detailed explanation of how to do it:
What Does Updating Weights Mean?
Updating weights and biases involves adjusting them in the direction that reduces the error of the network’s predictions. This is done using optimization techniques like gradient descent. Essentially, you are fine-tuning the parameters to make the neural network’s predictions more accurate.
How to Update Weights
- Calculate Gradients:
- Gradients are the changes needed for each weight and bias. They tell us how to adjust the parameters to reduce the error. During backpropagation, you calculate these gradients.
- Apply Updates:
- Learning Rate: This is a small number that controls how big a step you take when adjusting weights. A smaller learning rate means more gradual changes, while a larger learning rate means bigger steps.
- Update Weights and Biases: Use the gradients and learning rate to update the weights and biases. The general idea is to subtract a fraction of the gradient from the current value of each weight and bias.
Code Example
Here’s a Python code snippet showing how to update the weights and biases:
import numpy as np
def update_weights(weights_input_hidden, biases_hidden, weights_hidden_output, biases_output, output_delta, hidden_delta, X, learning_rate):
# Update weights and biases for the output layer
weights_hidden_output -= learning_rate * np.dot(hidden_layer_output.T, output_delta)
biases_output -= learning_rate * np.sum(output_delta, axis=0, keepdims=True)
# Update weights and biases for the hidden layer
weights_input_hidden -= learning_rate * np.dot(X.T, hidden_delta)
biases_hidden -= learning_rate * np.sum(hidden_delta, axis=0, keepdims=True)
return weights_input_hidden, biases_hidden, weights_hidden_output, biases_output
# Example learning rate
learning_rate = 0.01
weights_input_hidden, biases_hidden, weights_hidden_output, biases_output = update_weights(weights_input_hidden, biases_hidden, weights_hidden_output, biases_output, output_delta, hidden_delta, X, learning_rate)
Explanation of the Code
update_weightsFunction:- Inputs:
weights_input_hidden,biases_hidden,weights_hidden_output,biases_output: Current weights and biases in the network.output_delta,hidden_delta: Gradients calculated during backpropagation.X: Input data.learning_rate: Determines the size of the update step.
- Update Weights and Biases:
- For the Output Layer:
- Weights:
weights_hidden_output -= learning_rate * np.dot(hidden_layer_output.T, output_delta)- This calculates how much to adjust the weights by taking the dot product of the hidden layer’s output and the output delta, scaled by the learning rate.
- Biases:
biases_output -= learning_rate * np.sum(output_delta, axis=0, keepdims=True)- This adjusts the biases by summing the output deltas and scaling by the learning rate.
- Weights:
- For the Hidden Layer:
- Weights:
weights_input_hidden -= learning_rate * np.dot(X.T, hidden_delta)- This updates the weights by taking the dot product of the input data and the hidden delta, scaled by the learning rate.
- Biases:
biases_hidden -= learning_rate * np.sum(hidden_delta, axis=0, keepdims=True)- This adjusts the biases by summing the hidden deltas and scaling by the learning rate.
- Weights:
- For the Output Layer:
- Inputs:
- Learning Rate:
- Set to
0.01in this example. It controls how much to adjust weights and biases during each update. If the learning rate is too high, the network might not converge well. If it’s too low, learning might be very slow.
- Set to
Updating weights and biases is a crucial part of training a neural network. It involves using gradients calculated during backpropagation and a learning rate to adjust the parameters so the network’s predictions improve over time. By continually updating the weights and biases based on the error, the neural network becomes better at making accurate predictions.
Training the Neural Network
Training a neural network involves several key steps to ensure the network learns effectively and performs well on new data. Here’s a detailed guide to help you through the process:
Step 1: Preparing the Data
Before you start training your neural network, you need to prepare your data. Properly prepared data can significantly improve how well the network learns and performs.
1. Data Normalization
What is Normalization? Normalization is the process of scaling your data to fit within a specific range, usually between 0 and 1. This helps the neural network learn more effectively by ensuring that all input features are on a similar scale.
Why Normalize Data?
- Improves Learning: Neural networks often perform better when the input data is on a similar scale. Normalization helps the network converge faster and improves training efficiency.
- Avoids Issues: Large differences in scale can cause numerical instability and make the learning process slow or difficult.
How to Normalize Data: You use a technique called Min-Max Scaling which transforms each feature to fit within the range [0, 1].
Code Example
import numpy as np
from sklearn.preprocessing import MinMaxScaler
# Example dataset with features and target labels
X = np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6], [0.7, 0.8, 0.9]])
y = np.array([[0], [1], [0]])
# Create a scaler object
scaler = MinMaxScaler()
# Fit the scaler to the data and transform the data
X_normalized = scaler.fit_transform(X)
MinMaxScaler: This tool scales your features so that they fall between 0 and 1.fit_transform: This method first calculates the scaling parameters and then applies the scaling to your data.
2. Data Splitting
What is Data Splitting?
Data splitting involves dividing your dataset into separate parts: one for training the network and one for testing its performance. This ensures that you can evaluate how well your network performs on new, unseen data.
Why Split the Data?
- Training Set: Used to train the neural network. The model learns from this data.
- Testing Set: Used to evaluate how well the network performs after training. This helps in assessing the generalization of the model.
How to Split Data: You usually divide the data into a training set and a testing set. A common practice is to use around 80% of the data for training and 20% for testing.
Code Example
from sklearn.model_selection import train_test_split
# Split the normalized data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X_normalized, y, test_size=0.2, random_state=42)
train_test_split: This function divides the data into training and testing sets.test_size=0.2: Specifies that 20% of the data should be used for testing.random_state=42: Ensures that the split is reproducible. Using the same seed value will give you the same split every time.
By preparing your data through normalization and splitting, you set the stage for effective training and evaluation of your neural network. This ensures that your network learns well and performs accurately on unseen data.
Training Loop: The Heart of Neural Network Learning
The training loop is the core of the neural network learning process. It involves repeatedly updating the network based on the data to improve its performance. Here’s a detailed breakdown of how it works and how you can implement it in Python.
What is the Training Loop?
The training loop is a repetitive process where the neural network learns from the data by continuously improving its performance. This involves several key steps:
- Forward Propagation: The network makes predictions based on the input data.
- Compute Loss: The network calculates the error between its predictions and the actual results.
- Backpropagation: The network adjusts its internal parameters (weights and biases) based on the error.
- Update Weights: The network updates its weights and biases to reduce the error.
This loop runs for a set number of iterations, called epochs, where each epoch is a complete pass through the training data.
We have already explored backward and forward propagation, loss computation, and update weights in detail. Now, let’s see how to implement these in Python code.
In-Depth Overview of Each Step
1. Forward Propagation
What Happens Here? In forward propagation, the input data is fed through the network’s layers to produce an output. This output is the network’s prediction.
Why is it Important? Forward propagation allows the network to generate predictions based on the current state of its weights and biases. This step is essential for evaluating how well the network is performing.
Code Example
output = forward_propagation(X_train, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
2. Compute Loss
What Happens Here? After obtaining predictions, the network computes the loss or error using a loss function. The loss function measures how far the network’s predictions are from the actual values.
Why is it Important? The loss tells us how well or poorly the network is performing. Lower loss indicates better performance. The goal is to minimize this loss through training.
Code Example
loss = compute_loss(y_train, output)
3. Backpropagation
What Happens Here? Backpropagation calculates the gradients of the loss function with respect to the weights and biases. It helps in determining how to adjust these parameters to reduce the loss.
Why is it Important? This step is crucial for learning. By understanding how much each parameter contributed to the loss, the network can make precise adjustments to improve performance.
Code Example
output_delta, hidden_delta = backpropagation(X_train, y_train, output, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
4. Update Weights
What Happens Here? The network updates its weights and biases using the gradients calculated during backpropagation. This step is done using an optimization technique like gradient descent.
Why is it Important? Updating weights helps the network reduce the loss. This is how the network learns from its mistakes and improves its predictions over time.
Code Example
weights_input_hidden, biases_hidden, weights_hidden_output, biases_output = update_weights(weights_input_hidden, biases_hidden, weights_hidden_output, biases_output, output_delta, hidden_delta, X_train, learning_rate)
Putting It All Together
Here’s how you combine these steps into a training loop:
Code Example
def train_network(X_train, y_train, epochs, learning_rate):
for epoch in range(epochs):
# Forward propagation
output = forward_propagation(X_train, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
# Compute loss
loss = compute_loss(y_train, output)
# Backpropagation
output_delta, hidden_delta = backpropagation(X_train, y_train, output, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
# Update weights
weights_input_hidden, biases_hidden, weights_hidden_output, biases_output = update_weights(weights_input_hidden, biases_hidden, weights_hidden_output, biases_output, output_delta, hidden_delta, X_train, learning_rate)
# Print loss every 100 epochs
if epoch % 100 == 0:
print(f'Epoch {epoch}, Loss: {loss}')
# Example training
epochs = 1000
learning_rate = 0.01
train_network(X_train, y_train, epochs, learning_rate)
By following these steps and running the loop for a specified number of epochs, the network gradually learns and improves its predictions, becoming more accurate over time.
Monitoring Training Progress: Understanding How Well Your Neural Network is Learning
Monitoring the training progress of your neural network is essential for ensuring that your model is learning effectively. This process involves visualizing metrics like loss and accuracy to assess how well your model is performing and if any adjustments are needed. Here’s a detailed look at how you can do this:
Why Monitor Training Progress?
- Track Learning: By monitoring the loss and accuracy, you can see if your network is learning and improving over time. A decreasing loss indicates that the model is learning to make better predictions.
- Detect Issues: If the loss isn’t decreasing as expected or if it starts to increase, it may indicate problems such as overfitting, underfitting, or issues with the learning rate.
- Fine-Tune Parameters: Visualizing training progress helps you adjust hyperparameters like the learning rate or the number of epochs to optimize the training process.
How to Monitor Training Progress
1. Plotting Loss Over Epochs
Loss is a measure of how well the network’s predictions match the actual results. By plotting the loss over the epochs, you can visualize how the loss changes as the network learns.
Code Example
import matplotlib.pyplot as plt
def plot_training_progress(losses):
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Over Epochs')
plt.show()
2. Integrating Progress Monitoring into Training
During training, you need to collect the loss values at each epoch and then plot them. Here’s how you can integrate this into your training loop:
Code Example
def train_network_with_progress(X_train, y_train, epochs, learning_rate):
losses = [] # List to store loss values for each epoch
for epoch in range(epochs):
# Forward propagation to get predictions
output = forward_propagation(X_train, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
# Compute the loss
loss = compute_loss(y_train, output)
losses.append(loss) # Store loss for this epoch
# Backpropagation to calculate gradients
output_delta, hidden_delta = backpropagation(X_train, y_train, output, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
# Update weights based on the gradients
weights_input_hidden, biases_hidden, weights_hidden_output, biases_output = update_weights(weights_input_hidden, biases_hidden, weights_hidden_output, biases_output, output_delta, hidden_delta, X_train, learning_rate)
# Print loss every 100 epochs for feedback
if epoch % 100 == 0:
print(f'Epoch {epoch}, Loss: {loss}')
# Plot the training progress after the loop is finished
plot_training_progress(losses)
train_network_with_progress(X_train, y_train, epochs, learning_rate) Function: This function trains the network and monitors progress.
losses = []: Initializes a list to store loss values.losses.append(loss): Adds the loss value for each epoch to the list.plot_training_progress(losses): Plots the loss values after training is complete.
Why is This Important?
Visual Feedback: Seeing how the loss changes over time provides immediate feedback on the model’s performance. This helps you understand if the network is learning effectively or if there might be issues with the model or data.
Decision Making: By analyzing the plot, you can make informed decisions about adjusting hyperparameters or tweaking the model architecture to improve performance.
Model Evaluation: Regular monitoring helps you evaluate if the network is generalizing well to unseen data, ensuring that it performs well not just on training data but also on test data.
In summary, monitoring the training progress through visualizing metrics like loss helps you track the learning process, identify potential issues, and make necessary adjustments to improve your neural network’s performance.
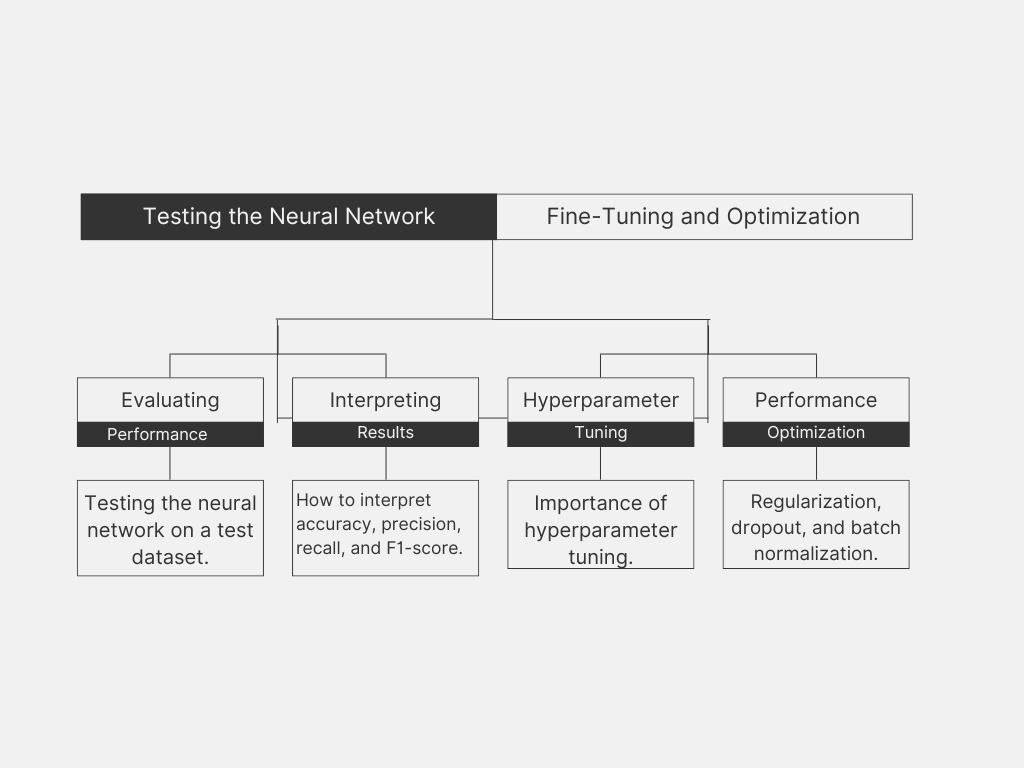
Evaluating Your Neural Network: Testing Performance with New Data
Once your neural network is trained, the next crucial step is to test its performance to ensure it can make accurate predictions on new, unseen data. This process involves evaluating how well the network generalizes to data it hasn’t encountered during training. Here’s a detailed guide on how to do this:
Why Test Your Neural Network?
- Assess Generalization: Testing with a separate dataset (test dataset) helps evaluate how well the network has learned to generalize from the training data to new, unseen data.
- Measure Accuracy: Testing provides insights into the network’s accuracy, which indicates the proportion of correct predictions out of the total predictions.
- Identify Overfitting: A significant difference in performance between the training and test datasets may suggest that the model is overfitting, meaning it performs well on training data but poorly on new data.
How to Test Your Neural Network
1. Prepare Your Test Data
Ensure that your test data is separate from the training data. This test dataset should not be used during the training process to provide a true evaluation of the network’s performance.
2. Forward Propagation on Test Data
Forward propagation involves passing the test data through the network to get predictions. This step processes the test inputs using the trained weights and biases.
Code Example
def test_network(X_test, y_test, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output):
# Forward propagation on test data
predictions = forward_propagation(X_test, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
# Convert predictions to binary labels (for classification)
predictions_binary = (predictions > 0.5).astype(int)
# Calculate accuracy
accuracy = np.mean(predictions_binary == y_test)
return predictions_binary, accuracy
# Example test data
predictions, accuracy = test_network(X_test, y_test, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)
print(f'Test Accuracy: {accuracy * 100:.2f}%')
Explanation of the Code
- Forward Propagation: The function
forward_propagation(X_test, weights_input_hidden, biases_hidden, weights_hidden_output, biases_output)is used to pass the test data (X_test) through the network. This generates the network’s predictions for the test set. - Binary Predictions: Since we are dealing with a classification problem, the predictions are converted into binary labels (0 or 1). This is done by applying a threshold of 0.5 to the predictions: values greater than 0.5 are classified as 1, and values less than or equal to 0.5 are classified as 0.
predictions_binary = (predictions > 0.5).astype(int)
- Accuracy Calculation: Accuracy is calculated by comparing the binary predictions (
predictions_binary) to the actual test labels (y_test). The mean of the boolean array (where True = 1 and False = 0) provides the proportion of correct predictions.
accuracy = np.mean(predictions_binary == y_test)
- Print Accuracy: The accuracy is printed as a percentage to give a clear measure of how well the network performs on the test data.
print(f'Test Accuracy: {accuracy * 100:.2f}%')
Why These Steps Matter
Forward Propagation: This is where the network makes predictions on the test data. It’s crucial for evaluating how well the network generalizes its learning to new data.
Binary Predictions: Converting the network’s outputs to binary labels makes it easier to calculate performance metrics like accuracy, especially for classification tasks.
Accuracy Calculation: This metric tells you the proportion of correct predictions, giving a straightforward measure of how well the model performs. High accuracy means the network is effectively learning and generalizing, while low accuracy may indicate issues that need addressing.
Testing Your Network: By testing your neural network, you ensure that it can make accurate predictions on new data, which is vital for its practical application. Monitoring accuracy helps you understand the network’s performance and guide further improvements if needed.
Interpreting Neural Network Results: Understanding Key Metrics
When evaluating how well your neural network performs, you need to look at various metrics to get a comprehensive picture of its effectiveness. Here’s a detailed guide on the key metrics and how to interpret them:
Interpreting Neural Network Results: Understanding Key Metrics
When evaluating how well your neural network performs, you need to look at various metrics to get a comprehensive picture of its effectiveness. Here’s a detailed guide on the key metrics and how to interpret them:
Key Metrics
1. Accuracy
- What It Is: Accuracy is the percentage of correctly predicted results out of all predictions made. It’s a straightforward measure of overall performance.
- Interpretation: High accuracy indicates that the network is making many correct predictions relative to the total number of predictions. However, accuracy alone might not be sufficient, especially in cases where the dataset is imbalanced (e.g., many more negative samples than positive ones).
Example
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, predictions_binary)
print(f'Accuracy: {accuracy:.2f}')
2. Precision
- What It Is: Precision measures the proportion of positive predictions that were actually correct. It answers the question: “Of all the times the network predicted a positive result, how often was it correct?”
- Interpretation: High precision means that when the network predicts a positive outcome, it is likely to be correct. This metric is crucial when the cost of false positives (incorrect positive predictions) is high.
Example
from sklearn.metrics import precision_score
precision = precision_score(y_test, predictions_binary)
print(f'Precision: {precision:.2f}')
3. Recall
- What It Is: Recall measures the proportion of actual positives that were correctly identified by the network. It answers the question: “Of all the actual positive cases, how many did the network correctly identify?”
- Interpretation: High recall means that the network is good at finding positive cases, but it might also include more false positives. This metric is important when missing a positive case (false negative) has a high cost.
Example
from sklearn.metrics import recall_score
recall = recall_score(y_test, predictions_binary)
print(f'Recall: {recall:.2f}')
4. F1-Score
- What It Is: The F1-score is the harmonic mean of precision and recall. It provides a single metric that balances both precision and recall.
- Interpretation: The F1-score is useful when you need to balance precision and recall, especially in situations where both false positives and false negatives are costly. It gives a better measure of the network’s performance when you need to consider both aspects together.
Example
from sklearn.metrics import f1_score
f1 = f1_score(y_test, predictions_binary)
print(f'F1 Score: {f1:.2f}')
By computing and analyzing these metrics, you can gain a well-rounded understanding of how your neural network performs:
- Accuracy gives an overall measure of performance.
- Precision tells you how often positive predictions are correct.
- Recall shows how well the network identifies positive cases.
- F1-Score balances precision and recall into one metric, useful when both are important.
These metrics help you assess the quality of your neural network’s predictions and make informed decisions about how to improve it.
Fine-Tuning and Optimization: Enhancing Neural Network Performance
Once you’ve successfully Evaluating Your Neural Network, the next step is to further improve its performance through fine-tuning and optimization. This involves adjusting various settings and techniques to make your model more accurate and efficient. Here’s a detailed guide on how to approach this process:
Hyperparameter Tuning
What is Hyperparameter Tuning?
Hyperparameter tuning is the process of selecting the best set of parameters that are not learned from the data but are set before the training process begins. These parameters are crucial as they control various aspects of the training process and the network’s architecture. Examples include:
- Learning Rate: Determines how much to adjust the weights with each update.
- Number of Epochs: Specifies how many times the training process will iterate over the entire dataset.
- Batch Size: Defines how many samples are processed before updating the weights.
- Number of Layers and Neurons: Specifies the architecture of the neural network, such as how many layers and how many neurons in each layer.
Why is it Important?
Proper tuning of these hyperparameters can significantly enhance your model’s performance. It helps the network to:
- Learn Effectively: Fine-tuning helps the network learn from the data more efficiently and accurately.
- Generalize Well: It improves the network’s ability to perform well on new, unseen data, avoiding issues like overfitting or underfitting.
Practical Tips for Hyperparameter Tuning
- Learning Rate:
- What It Is: The learning rate controls how big of a step you take in adjusting the weights with each iteration.
- Impact: A higher learning rate can speed up convergence but might overshoot the optimal solution. A lower learning rate provides more precise updates but can slow down convergence.
- Tip: Start with a moderate learning rate and adjust based on how well the network is learning.
- Number of Epochs:
- What It Is: The number of epochs defines how many times the entire dataset is used to update the weights.
- Impact: More epochs generally mean better learning, but too many epochs can lead to overfitting (where the model performs well on the training data but poorly on new data).
- Tip: Use techniques like early stopping to halt training when the performance on the validation set starts to degrade.
- Batch Size:
- What It Is: Batch size is the number of training samples processed before the model’s weights are updated.
- Impact: Smaller batch sizes can lead to more generalization and stability in training. Larger batch sizes can make the training faster but might lead to overfitting.
- Tip: Experiment with different batch sizes to find the one that provides the best trade-off between training time and model performance.
Code Example: Grid Search for Hyperparameter Tuning
Grid search is a popular method to find the optimal hyperparameters by testing various combinations. Here’s how you can use grid search with a neural network in Python:
from sklearn.model_selection import GridSearchCV
from sklearn.neural_network import MLPClassifier
# Define the parameter grid
param_grid = {
'hidden_layer_sizes': [(10,), (20,), (30,)],
'activation': ['tanh', 'relu'],
'solver': ['sgd', 'adam'],
'alpha': [0.0001, 0.001, 0.01],
'learning_rate': ['constant', 'adaptive'],
}
# Create a neural network model
mlp = MLPClassifier(max_iter=1000)
# Perform grid search
grid_search = GridSearchCV(estimator=mlp, param_grid=param_grid, cv=3)
grid_search.fit(X_train, y_train)
# Get the best parameters
best_params = grid_search.best_params_
print(f'Best Hyperparameters: {best_params}')
Explanation of the Code
- Parameter Grid: The
param_griddictionary contains different hyperparameters and their possible values that you want to test. - MLPClassifier: This is a neural network model provided by scikit-learn.
- GridSearchCV: This performs an exhaustive search over the specified parameter values. It evaluates the performance of the model for each combination of hyperparameters using cross-validation.
- Best Parameters: After running grid search, the
best_params_attribute provides the set of hyperparameters that resulted in the best model performance.
Performance Optimization: Enhancing Neural Network Efficiency
To get the best performance out of your neural network, you can employ several optimization techniques. These techniques help improve accuracy, speed up training, and ensure that your model generalizes well to new data. Here’s a detailed explanation of some key techniques:
1. Regularization
What is Regularization?
Regularization is a technique used to prevent overfitting, which occurs when a model learns the training data too well, including its noise and outliers. Overfitting makes the model perform poorly on new, unseen data.
How Does It Work?
Regularization adds a penalty to the loss function for larger weights. This penalty discourages the model from fitting the training data too closely and helps it to generalize better to new data.
Code Example
from sklearn.neural_network import MLPClassifier
# Create a model with regularization
model = MLPClassifier(alpha=0.001, max_iter=1000) # alpha is the regularization parameter
model.fit(X_train, y_train)
Explanation:
alpha: This parameter controls the amount of regularization. A higher alpha value increases the penalty for large weights.max_iter: Specifies the number of iterations (epochs) for training.
Regularization helps maintain a balance between fitting the data and keeping the model simple, improving its ability to handle new data.
2. Dropout
What is Dropout?
Dropout is a regularization technique used to prevent overfitting by randomly “dropping out” or deactivating a portion of neurons during each training iteration.
How Does It Work?
During training, dropout randomly sets a fraction of the neurons to zero, meaning they don’t participate in the forward and backward passes for that iteration. This prevents the network from becoming overly dependent on specific neurons, which helps it generalize better.
Code Example (using TensorFlow/Keras)
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
# Create a neural network model
model = Sequential([
Dense(64, activation='relu', input_shape=(input_size,)),
Dropout(0.5), # Dropout layer with a 50% dropout rate
Dense(32, activation='relu'),
Dense(output_size, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=10, batch_size=32)
Explanation:
Dropout(0.5): This specifies that 50% of the neurons will be randomly dropped during training. The dropout rate can be adjusted based on the network’s complexity and the dataset.
Dropout helps prevent overfitting by ensuring that the network doesn’t rely too heavily on any particular set of neurons, encouraging a more strong model.
3. Batch Normalization
What is Batch Normalization?
Batch normalization is a technique used to improve the speed and stability of training by normalizing the outputs of each layer. It adjusts and scales activations during training to ensure that they maintain a consistent mean and variance.
How Does It Work?
Batch normalization normalizes the input to each layer by subtracting the batch mean and dividing by the batch standard deviation. This helps in stabilizing and accelerating the training process.
Code Example (using TensorFlow/Keras)
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, BatchNormalization
# Create a neural network model
model = Sequential([
Dense(64, activation='relu', input_shape=(input_size,)),
BatchNormalization(), # Batch normalization layer
Dense(32, activation='relu'),
Dense(output_size, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=10, batch_size=32)
Explanation
BatchNormalization(): This layer normalizes the output of the previous layer. It ensures that the distribution of activations remains stable during training.
Batch normalization improves training speed and helps the model converge faster by stabilizing the learning process.
By incorporating these techniques, you can create a more accurate and efficient neural network that performs well both on training data and unseen data.
Complete code to Building a Neural Network from Scratch to Solve the XOR Problem Using Python
Here’s a basic implementation of a simple feedforward neural network in Python:
import numpy as np
# Activation functions and their derivatives
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
def relu(x):
return np.maximum(0, x)
def relu_derivative(x):
return np.where(x > 0, 1, 0)
# Initialize network parameters
def initialize_parameters(input_dim, hidden_dim, output_dim):
np.random.seed(42)
W1 = np.random.randn(input_dim, hidden_dim) * np.sqrt(2.0 / input_dim)
b1 = np.zeros((1, hidden_dim))
W2 = np.random.randn(hidden_dim, output_dim) * np.sqrt(2.0 / hidden_dim)
b2 = np.zeros((1, output_dim))
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2
}
return parameters
# Forward propagation
def forward_propagation(X, parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(X, W1) + b1
A1 = relu(Z1)
Z2 = np.dot(A1, W2) + b2
A2 = sigmoid(Z2)
cache = {
"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2
}
return A2, cache
# Compute loss
def compute_loss(Y, A2):
m = Y.shape[0]
loss = -np.sum(Y * np.log(A2) + (1 - Y) * np.log(1 - A2)) / m
return loss
# Backward propagation
def backward_propagation(X, Y, parameters, cache):
m = X.shape[0]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2 - Y
dW2 = np.dot(A1.T, dZ2) / m
db2 = np.sum(dZ2, axis=0, keepdims=True) / m
dA1 = np.dot(dZ2, W2.T)
dZ1 = dA1 * relu_derivative(A1)
dW1 = np.dot(X.T, dZ1) / m
db1 = np.sum(dZ1, axis=0, keepdims=True) / m
grads = {
"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2
}
return grads
# Update parameters
def update_parameters(parameters, grads, learning_rate):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
W1 -= learning_rate * dW1
b1 -= learning_rate * db1
W2 -= learning_rate * dW2
b2 -= learning_rate * db2
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2
}
return parameters
# Training the neural network
def train_neural_network(X, Y, input_dim, hidden_dim, output_dim, num_iterations, learning_rate):
parameters = initialize_parameters(input_dim, hidden_dim, output_dim)
for i in range(num_iterations):
A2, cache = forward_propagation(X, parameters)
loss = compute_loss(Y, A2)
grads = backward_propagation(X, Y, parameters, cache)
parameters = update_parameters(parameters, grads, learning_rate)
if i % 1000 == 0:
print(f"Loss after iteration {i}: {loss}")
return parameters
# Making predictions
def predict(X, parameters):
A2, _ = forward_propagation(X, parameters)
predictions = (A2 > 0.5).astype(int)
return predictions
# Example Usage
if __name__ == "__main__":
# Sample data for XOR problem
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [1], [1], [0]])
# Network dimensions
input_dim = 2
hidden_dim = 10 # Increased number of neurons in the hidden layer
output_dim = 1
# Training the neural network
parameters = train_neural_network(X, Y, input_dim, hidden_dim, output_dim, num_iterations=10000, learning_rate=0.01)
# Making predictions
predictions = predict(X, parameters)
print("Predictions:")
print(predictions)
Output
Loss after iteration 0: 0.9060411745704565
Loss after iteration 1000: 0.528406430990051
Loss after iteration 2000: 0.45628637802258565
Loss after iteration 3000: 0.3721464705702542
Loss after iteration 4000: 0.2714371025032263
Loss after iteration 5000: 0.1847126755791574
Loss after iteration 6000: 0.12826228304741744
Loss after iteration 7000: 0.09373873854329356
Loss after iteration 8000: 0.0718495778805388
Loss after iteration 9000: 0.05729855913925554
Predictions:
[[0]
[1]
[1]
[0]]
Process finished with exit code 0Conclusion
Building a neural network from scratch using Python is a rewarding experience that helps you truly understand how these powerful models work. By putting together each part—from forward propagation to backpropagation—you get a hands-on look at the inner workings of neural networks. This approach not only improves your coding skills but also sets you up to handle more complex machine learning projects in the future. With this solid foundation, you’re ready to enter into advanced topics and apply neural networks to real-world problems.
Additional Resources
To continue your journey in learning about neural networks and improving your skills, here are some recommended readings, tools, and libraries:
Recommended Reading
- “Deep Learning” by Ian Goodfellow, Yoshua Bengio, and Aaron Courville:
- A comprehensive book that covers a wide range of topics in deep learning.
- “Neural Networks and Deep Learning” by Michael Nielsen:
- An accessible introduction to neural networks and deep learning, available for free online.
- “Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow” by Aurélien Géron:
- A practical guide to building and training neural networks with popular Python libraries.
Tools and Libraries
- TensorFlow:
- An open-source library developed by Google for building and training neural networks.
- Keras:
- A high-level neural networks API, written in Python and capable of running on top of TensorFlow, CNTK, or Theano.
- PyTorch:
- An open-source machine learning library developed by Facebook’s AI Research lab, known for its flexibility and ease of use.
- Scikit-Learn:
- A simple and efficient tool for data mining and data analysis, built on NumPy, SciPy, and Matplotlib.
- Google Colab:
- A free cloud service that provides Jupyter notebooks and access to GPUs, which is great for running machine learning experiments.
Libraries for Specific Tasks
- OpenCV:
- A library focused on computer vision tasks.
- NLTK:
- A library for natural language processing in Python.
- Pandas:
- A powerful data manipulation and analysis library.
By using these resources, you can deepen your understanding of neural networks and explore advanced topics and techniques.









Leave a Reply