Skip to content
Home » Blog » How to Write a Python Program to Find LCM

How to Write a Python Program to Find LCM

Complete Guide to Finding LCM in Python: 4 Methods with Examples and Interactive Quiz

Complete Guide to Finding LCM in Python: 4 Methods with Examples and Interactive Quiz

Master Python LCM calculation with proven methods, expert tips, and interactive examples perfect for competitive programming

Published: January 2025 | Reading Time: 15 minutes | Level: Beginner to Advanced

Table of Contents

Introduction

Why Learn LCM in Python Programming?

Learning LCM (Least Common Multiple) in Python is essential for competitive programming, algorithm design, and solving real-world synchronization problems. This comprehensive guide covers all methods from basic to advanced.

Finding the Least Common Multiple (LCM) is a fundamental mathematical operation that every Python programmer should master. Whether you’re preparing for coding interviews, competitive programming contests, or building real-world applications, understanding LCM calculation methods will give you a significant advantage.

In this comprehensive tutorial, we’ll explore four different methods to calculate LCM in Python, each with its own benefits and use cases. You’ll also get hands-on practice with our interactive calculator and test your knowledge with a challenging quiz.

What You’ll Learn:

  • 4 proven methods to calculate LCM in Python
  • When to use each method for optimal performance
  • Real-world applications and use cases
  • Common mistakes and how to avoid them
  • Latest shortcuts and expert tricks for 2025
  • Interactive examples and hands-on practice

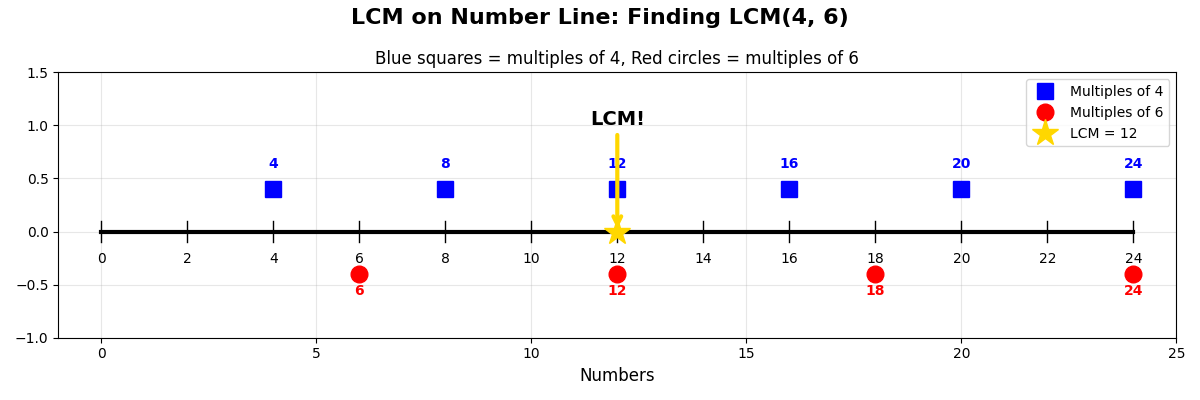
What is LCM in Programming and Mathematics?

Definition of LCM

Simple Definition

The Least Common Multiple (LCM) is the smallest positive number that can be divided by two or more numbers without leaving a remainder.

Basic LCM Examples

Numbers Multiples LCM Explanation
4, 6 4: 4, 8, 12, 16, 20, 24
6: 6, 12, 18, 24		 12 First common multiple
8, 12 8: 8, 16, 24, 32
12: 12, 24, 36		 24 Smallest shared multiple
15, 25 15: 15, 30, 45, 60, 75
25: 25, 50, 75		 75 Common multiple found

Understanding LCM is crucial for many programming scenarios. When you’re working with function parameters and return values in Python, you might need to synchronize different data processing cycles or handle periodic tasks.

Why Learn to Find LCM Using Python?

Use Cases in Software Development

Game Development

Synchronize animations, spawn enemies at regular intervals, create rhythm-based mechanics in games.

Task Scheduling

Schedule automated tasks, backup systems, and periodic maintenance operations efficiently.

Data Processing

Synchronize data streams, batch processing jobs, and real-time analytics systems.

Algorithm Design

Essential for machine learning algorithms and competitive programming solutions.

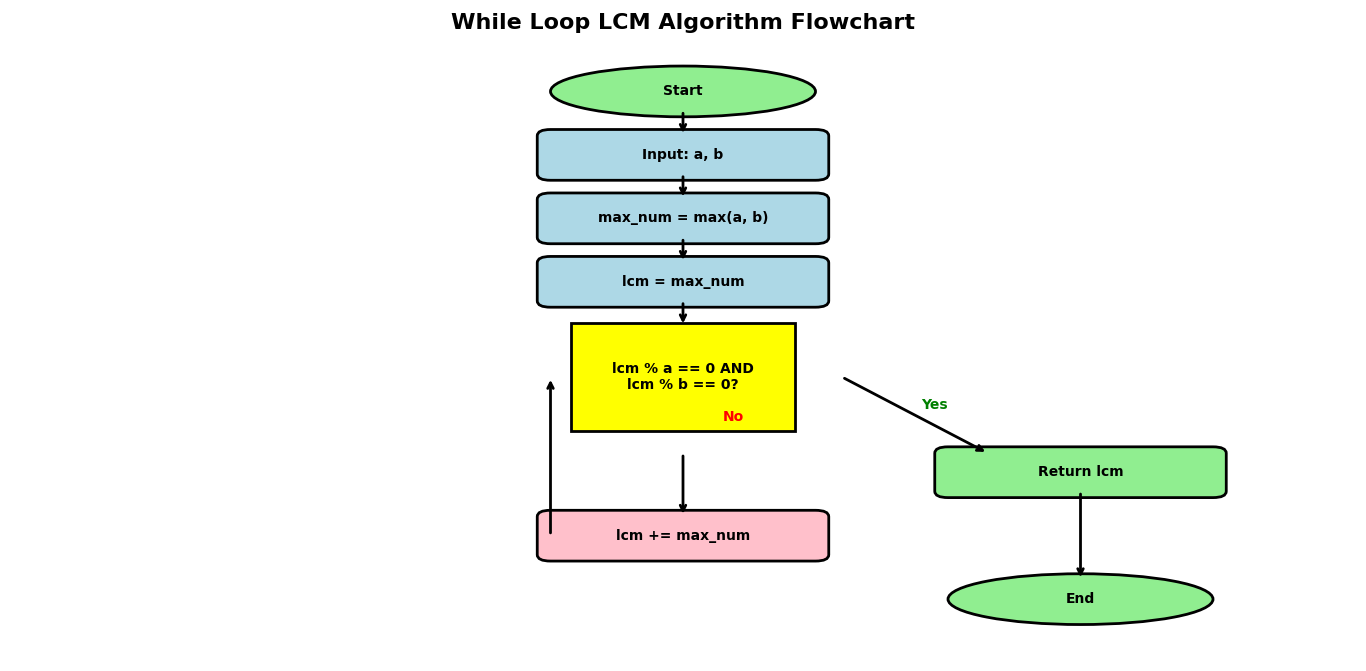
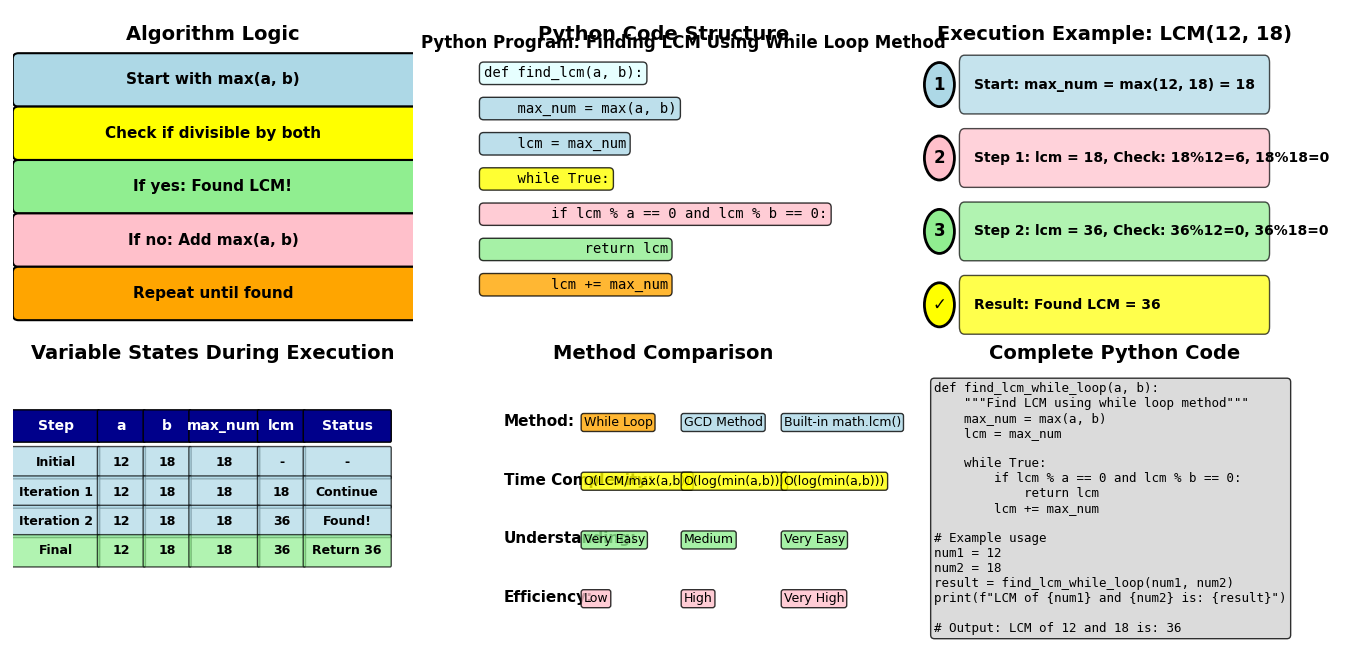
Python Program to Find LCM of Two Numbers Using While Loop

Simple Brute-Force Approach

The while loop method is the most intuitive approach for beginners. It systematically checks multiples until finding the LCM.

Method 1: Using While Loop to Find LCM
# Method 1: Using While Loop to Find LCM def find_lcm_while_loop(a, b): “”” Find LCM of two numbers using while loop This is the easiest method to understand! “”” # Start with the larger number max_num = max(a, b) lcm = max_num # Keep checking until we find LCM while True: if lcm % a == 0 and lcm % b == 0: return lcm lcm += max_num # Example usage num1 = 12 num2 = 18 result = find_lcm_while_loop(num1, num2) print(f”LCM of {num1} and {num2} is: {result}”) # Let’s trace through the steps: print(“\n— Step by step calculation —“) a, b = 12, 18 max_num = max(a, b) # 18 print(f”Starting with: {max_num}”) step = 1 lcm = max_num while True: print(f”Step {step}: Checking {lcm}”) if lcm % a == 0 and lcm % b == 0: print(f”Found LCM: {lcm}”) break else: print(f” {lcm} ÷ {a} = {lcm//a} remainder {lcm%a}”) print(f” {lcm} ÷ {b} = {lcm//b} remainder {lcm%b}”) lcm += max_num step += 1
Output:
LCM of 12 and 18 is: 36 — Step by step calculation — Starting with: 18 Step 1: Checking 18 18 ÷ 12 = 1 remainder 6 18 ÷ 18 = 1 remainder 0 Step 2: Checking 36 36 ÷ 12 = 3 remainder 0 36 ÷ 18 = 2 remainder 0 Found LCM: 36

When to Use

Best for: Learning purposes, small numbers, when you need to understand the step-by-step process

Time Complexity: O(max(a,b)) in worst case

Space Complexity: O(1)

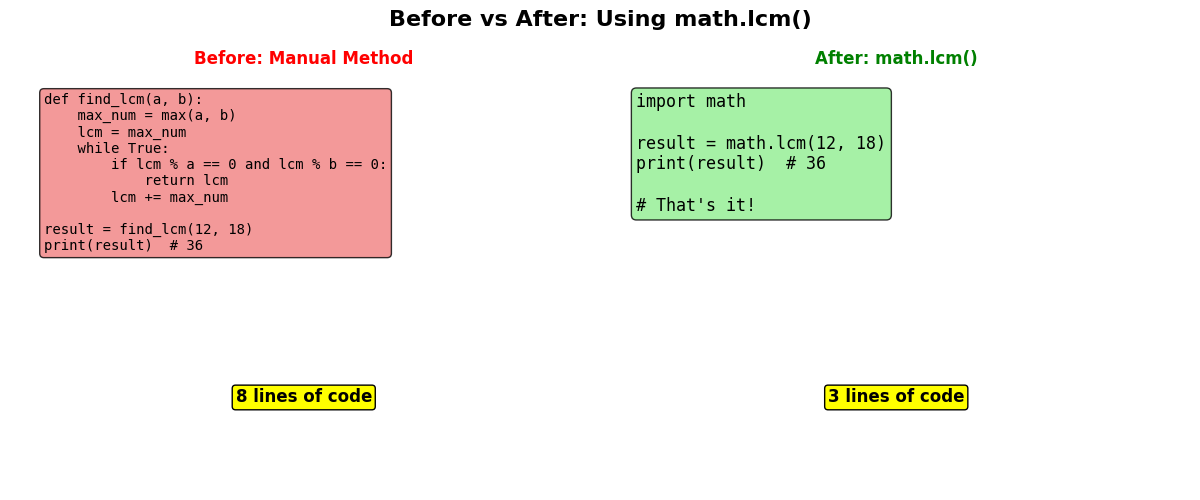
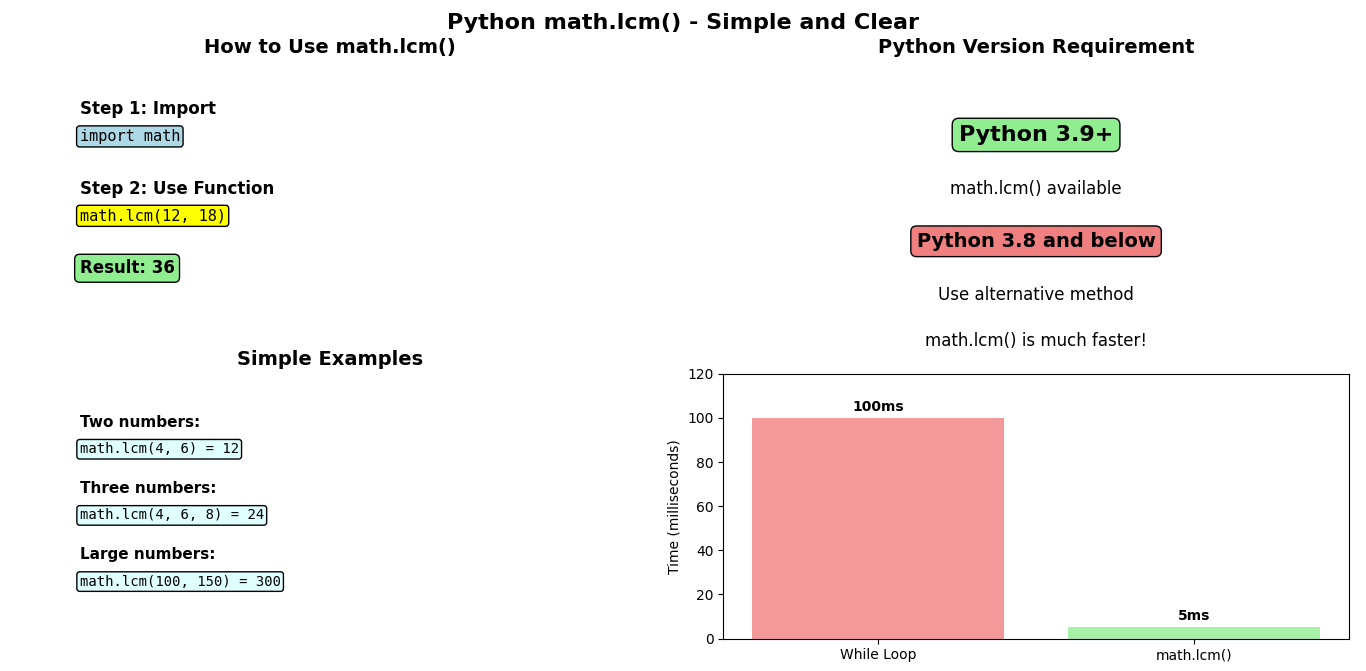
Shortcut Method: Using math.lcm() in Python 3.9 and Above

The Quickest Way to Find LCM

Python 3.9 introduced the built-in math.lcm() function, making LCM calculation incredibly simple and efficient.

Method 2: Using math.lcm() – Python 3.9+
# Method 2: Using math.lcm() – Python 3.9+ import math # For two numbers num1 = 12 num2 = 18 result = math.lcm(num1, num2) print(f”LCM of {num1} and {num2} is: {result}”) # For multiple numbers (super cool!) numbers = [12, 18, 24, 30] result_multiple = math.lcm(*numbers) print(f”LCM of {numbers} is: {result_multiple}”) # Real-world example: Task scheduling print(“\nReal Example: Task Scheduling”) task1_interval = 5 # Every 5 minutes task2_interval = 7 # Every 7 minutes task3_interval = 3 # Every 3 minutes sync_time = math.lcm(task1_interval, task2_interval, task3_interval) print(f”All tasks will run together every {sync_time} minutes!”) # Performance comparison import time def performance_test(): start = time.time() for i in range(10000): math.lcm(123, 456) end = time.time() print(f”math.lcm() executed 10,000 times in {end-start:.4f} seconds”)
Output:
LCM of 12 and 18 is: 36 LCM of [12, 18, 24, 30] is: 360 Real Example: Task Scheduling All tasks will run together every 105 minutes!

Advantages

  • Extremely fast and optimized
  • Handles multiple numbers natively
  • Built-in error handling
  • Perfect for production code

Limitation

Important: Only available in Python 3.9 and above. For older versions, use the GCD method below.

Using GCD to Find LCM in Python (Compatible with All Versions)

Efficient Mathematical Formula

This method uses the mathematical relationship: LCM(a,b) = (a × b) ÷ GCD(a,b)

Method 3: Using GCD to Find LCM (Works in all Python versions!)
# Method 3: Using GCD to Find LCM (Works in all Python versions!) import math def find_lcm_using_gcd(a, b): “”” Find LCM using the mathematical formula: LCM(a,b) = (a × b) ÷ GCD(a,b) “”” return abs(a * b) // math.gcd(a, b) # Example with step-by-step explanation num1 = 12 num2 = 18 print(f”Finding LCM of {num1} and {num2}”) print(f”Step 1: Calculate GCD({num1}, {num2})”) gcd_result = math.gcd(num1, num2) print(f” GCD = {gcd_result}”) print(f”Step 2: Apply formula: ({num1} × {num2}) ÷ {gcd_result}”) product = num1 * num2 print(f” Product = {product}”) lcm_result = product // gcd_result print(f” LCM = {product} ÷ {gcd_result} = {lcm_result}”) # Advanced: Custom GCD implementation for educational purposes def custom_gcd(a, b): “””Custom GCD using Euclidean algorithm””” while b: a, b = b, a % b return a def custom_lcm(a, b): “””Custom LCM using our custom GCD””” return abs(a * b) // custom_gcd(a, b) print(f”\nUsing custom implementation: {custom_lcm(12, 18)}”)
Output:
Finding LCM of 12 and 18 Step 1: Calculate GCD(12, 18) GCD = 6 Step 2: Apply formula: (12 × 18) ÷ 6 Product = 216 LCM = 216 ÷ 6 = 36 Using custom implementation: 36

Why Use GCD?

Mathematical Efficiency: This method is mathematically elegant and computationally efficient. It’s the foundation for most LCM implementations in programming libraries.

Time Complexity: O(log(min(a,b))) – much faster than the while loop method

This approach is essential when working with function definitions and calls in Python, especially in mathematical computing applications.

Efficient Way to Find LCM of Multiple Numbers in Python

Using reduce() with GCD-based LCM

When you need to find LCM of more than two numbers, the reduce() function provides an elegant solution.

Method 4: Using reduce() for Multiple Numbers
# Method 4: Using reduce() for Multiple Numbers (Works in ALL Python versions!) from functools import reduce import math def lcm_two_numbers(a, b): “””Find LCM of two numbers using GCD””” return abs(a * b) // math.gcd(a, b) def lcm_multiple_numbers(numbers): “”” Find LCM of multiple numbers using reduce() This applies our LCM function step by step to all numbers “”” return reduce(lcm_two_numbers, numbers) # Example: Let’s trace through the process numbers = [6, 8, 12, 16] print(f”Finding LCM of {numbers}”) print(“\nStep-by-step process using reduce():”) # Manual step-by-step to show how reduce works step1 = lcm_two_numbers(numbers[0], numbers[1]) # LCM(6, 8) print(f”Step 1: LCM({numbers[0]}, {numbers[1]}) = {step1}”) step2 = lcm_two_numbers(step1, numbers[2]) # LCM(24, 12) print(f”Step 2: LCM({step1}, {numbers[2]}) = {step2}”) step3 = lcm_two_numbers(step2, numbers[3]) # LCM(24, 16) print(f”Step 3: LCM({step2}, {numbers[3]}) = {step3}”) # Using our function result = lcm_multiple_numbers(numbers) print(f”\nFinal LCM = {result}”) # Real-world example: Synchronizing multiple processes print(“\nReal-world Example: Process Synchronization”) process_intervals = [3, 5, 7, 11] # Different process intervals in seconds sync_interval = lcm_multiple_numbers(process_intervals) print(f”Processes with intervals {process_intervals} will sync every {sync_interval} seconds”) # One-liner for competitive programming lcm_oneliner = lambda nums: reduce(lambda a, b: abs(a*b)//math.gcd(a,b), nums) print(f”One-liner result: {lcm_oneliner([6, 8, 12, 16])}”)
Output:
Finding LCM of [6, 8, 12, 16] Step-by-step process using reduce(): Step 1: LCM(6, 8) = 24 Step 2: LCM(24, 12) = 24 Step 3: LCM(24, 16) = 48 Final LCM = 48 Real-world Example: Process Synchronization Processes with intervals [3, 5, 7, 11] will sync every 1155 seconds One-liner result: 48

Works Across All Versions of Python

This method is perfect for competitive programming and works reliably across all Python versions. It’s especially useful in data analysis scenarios where you need to synchronize multiple data streams.

Interactive LCM Calculator

Try It Yourself: LCM Calculator

Test Your Knowledge: Interactive Quiz

What is the LCM of 15 and 25?
50
75
100
125

Practice with Python Playground

Try the code examples yourself in this interactive Python environment:

Practice Exercises:

  1. Implement the while loop method for numbers 14 and 21
  2. Create a function that finds LCM of three numbers using the GCD method
  3. Write a program that finds LCM of a list of numbers using reduce()
  4. Compare performance of different methods with large numbers

Common Mistakes and Quick Fixes

Using math.lcm() in Older Python Versions

Problem:

AttributeError: module 'math' has no attribute 'lcm'

Solution:

Use the GCD method for Python versions below 3.9:

import math lcm = lambda a, b: abs(a*b) // math.gcd(a, b)

Forgetting to Convert Input Strings to Integers

Problem:

TypeError: unsupported operand type(s) for %: 'str' and 'int'

Solution:

num1 = int(input(“Enter first number: “)) num2 = int(input(“Enter second number: “))

Handling Zero Values

Problem:

LCM with zero should return zero, but some implementations may fail

Solution:

def safe_lcm(a, b): if a == 0 or b == 0: return 0 return abs(a * b) // math.gcd(a, b)

Interview Tips and Coding Tricks

Fast Input/Output for Competitive Programming

Optimized I/O for Competitive Programming
# Fast I/O for competitive programming import sys import math from functools import reduce # Fast input def fast_input(): return sys.stdin.readline().strip() # One-liner LCM for two numbers lcm2 = lambda a, b: abs(a*b) // math.gcd(a, b) # One-liner LCM for multiple numbers lcm_multi = lambda nums: reduce(lcm2, nums) # Template for competitive programming def solve(): # Read number of test cases t = int(fast_input()) for _ in range(t): # Read two numbers a, b = map(int, fast_input().split()) # Calculate and print LCM print(lcm2(a, b)) # Alternative: Handle multiple numbers in one line def solve_multiple(): nums = list(map(int, input().split())) print(lcm_multi(nums)) # Example usage if __name__ == “__main__”: solve()

One-Liner for Two Numbers (GCD Method)

Memory Tip: lcm = lambda a, b: a*b // math.gcd(a, b)

This one-liner is perfect for coding interviews and competitive programming.

Handle Arbitrary-Length Input with Map

Flexible Input Handling
# Handle any number of inputs def lcm_from_input(): “”” Reads numbers from input and calculates LCM Works for any number of inputs “”” numbers = list(map(int, input(“Enter numbers separated by spaces: “).split())) if len(numbers) < 2: return "Need at least 2 numbers" result = numbers[0] for num in numbers[1:]: result = abs(result * num) // math.gcd(result, num) return result # Advanced: Error handling version def robust_lcm_input(): try: numbers = list(map(int, input().split())) if not numbers: raise ValueError("No numbers provided") if len(numbers) == 1: return numbers[0] return reduce(lambda a, b: abs(a*b) // math.gcd(a, b), numbers) except ValueError as e: return f"Error: {e}" # Usage examples print(lcm_from_input()) # User inputs: 12 18 24 print(robust_lcm_input()) # Handles errors gracefully

Latest Shortcut Methods and Expert Tricks (2025 Edition)

Python 3.12+ Optimizations

Latest Python 3.12+ Features
# Python 3.12+ optimized implementations import math from typing import List from functools import reduce # Type-hinted version for better IDE support def lcm_typed(a: int, b: int) -> int: “””Type-hinted LCM function for better code quality””” return abs(a * b) // math.gcd(a, b) def lcm_multiple_typed(numbers: List[int]) -> int: “””Type-hinted multiple number LCM””” return reduce(lcm_typed, numbers) # Using walrus operator (Python 3.8+) def lcm_with_validation(a: int, b: int) -> int: “””LCM with inline validation using walrus operator””” if (gcd_val := math.gcd(a, b)) == 0: return 0 return abs(a * b) // gcd_val # Performance-optimized version with caching from functools import lru_cache @lru_cache(maxsize=1000) def cached_lcm(a: int, b: int) -> int: “””Cached LCM for repeated calculations””” return abs(a * b) // math.gcd(a, b) # Batch processing for large datasets def batch_lcm(number_pairs: List[tuple]) -> List[int]: “””Process multiple LCM calculations efficiently””” return [lcm_typed(a, b) for a, b in number_pairs] # Example usage pairs = [(12, 18), (15, 25), (8, 12), (20, 30)] results = batch_lcm(pairs) print(f”Batch LCM results: {results}”) # Memory-efficient generator for large datasets def lcm_generator(pairs): “””Memory-efficient LCM calculation for large datasets””” for a, b in pairs: yield abs(a * b) // math.gcd(a, b) # Usage with generator large_pairs = [(i, i+1) for i in range(1, 1000)] lcm_results = list(lcm_generator(large_pairs)) print(f”Processed {len(lcm_results)} LCM calculations”)

Advanced Competitive Programming Tricks

Bit Manipulation Optimization
# For powers of 2, use bit operations def lcm_power_of_2(a, b): return max(a, b) if (a & (a-1)) == 0 and (b & (b-1)) == 0 else lcm_typed(a, b)
Prime Factorization Method
# Advanced: Using prime factorization def prime_factors(n): factors = {} d = 2 while d * d <= n: while n % d == 0: factors[d] = factors.get(d, 0) + 1 n //= d d += 1 if n > 1: factors[n] = factors.get(n, 0) + 1 return factors
NumPy Integration
# For data science applications import numpy as np lcm_vectorized = np.vectorize(lambda a, b: abs(a*b) // math.gcd(a, b)) result = lcm_vectorized([12, 15], [18, 25])
Parallel Processing
# For large datasets from multiprocessing import Pool def parallel_lcm(pairs): with Pool() as pool: return pool.starmap(lcm_typed, pairs)

Expert Memory Techniques

Mnemonic for LCM Formula

“Product over GCD” – Remember: LCM = (A × B) ÷ GCD(A, B)

“Least Common, Greatest Divisor” – LCM uses GCD in its calculation

Frequently Asked Questions

What’s the difference between LCM and GCD?

LCM (Least Common Multiple) is the smallest number that both numbers can divide into evenly.

GCD (Greatest Common Divisor) is the largest number that can divide both numbers evenly.

Example: For 12 and 18:

  • LCM(12, 18) = 36 (smallest number divisible by both)
  • GCD(12, 18) = 6 (largest number that divides both)

They’re mathematically related: LCM(a,b) × GCD(a,b) = a × b

Which LCM method is fastest for large numbers?

For Python 3.9+: Use math.lcm() – it’s highly optimized and handles edge cases.

For older versions: Use the GCD method: abs(a*b) // math.gcd(a, b)

Performance ranking:

  1. math.lcm() (fastest, Python 3.9+)
  2. GCD method (fast, all versions)
  3. Optimized while loop (medium)
  4. Basic while loop (slowest)
How do I find LCM of more than 2 numbers efficiently?

Best method: Use reduce() with the GCD-based LCM function:

from functools import reduce import math def lcm_multiple(numbers): return reduce(lambda a, b: abs(a*b) // math.gcd(a, b), numbers) # Example result = lcm_multiple([12, 18, 24, 30]) # Returns 360

For Python 3.9+: math.lcm(*numbers) is even simpler!

What happens when I calculate LCM with zero?

Mathematical rule: LCM of any number with 0 is 0.

Why? Zero is divisible by every number, so the “least common multiple” involving zero is zero itself.

print(math.lcm(12, 0)) # Output: 0 print(math.lcm(0, 5)) # Output: 0

In custom functions: Always handle zero cases explicitly to avoid division by zero errors.

Can I use LCM with negative numbers?

Yes! LCM is typically defined for positive results, even with negative inputs.

print(math.lcm(-12, 18)) # Output: 36 print(math.lcm(-12, -18)) # Output: 36

Best practice: Use abs() in custom implementations to ensure positive results:

def safe_lcm(a, b): return abs(a * b) // math.gcd(abs(a), abs(b))
What are real-world applications of LCM in programming?

Common applications include:

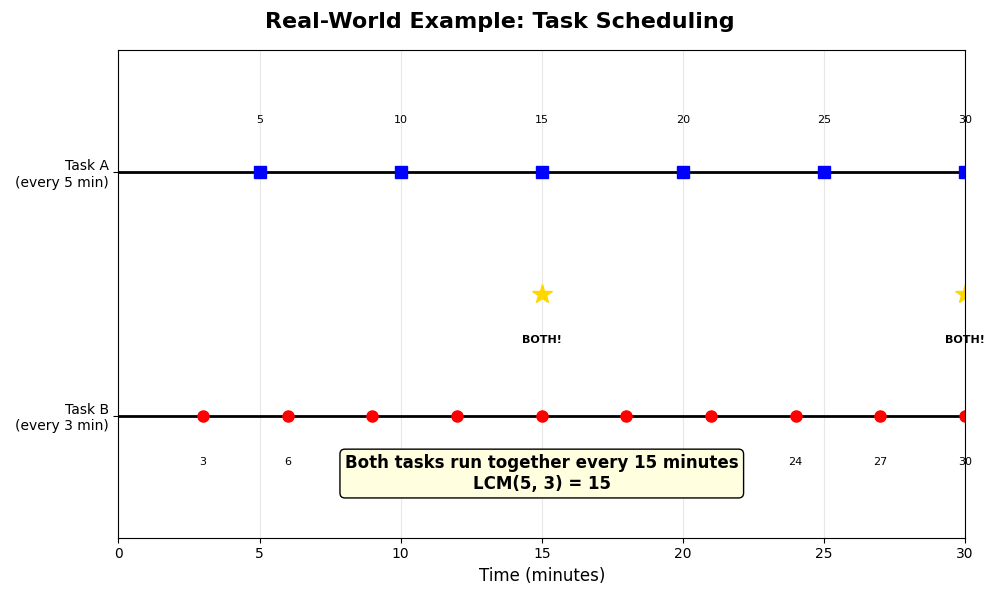
  • Task Scheduling: Finding when multiple periodic tasks sync up
  • Game Development: Synchronizing animations and spawning cycles
  • Data Processing: Aligning different sampling rates in time series data
  • Audio/Video: Synchronizing frame rates and sample rates
  • Cryptocurrency: Block generation timing in blockchain systems
  • Network Protocols: Synchronizing transmission intervals

Understanding LCM is crucial for building Flask applications that need to handle periodic tasks efficiently.

How do I optimize LCM calculations for competitive programming?

Key optimization strategies:

  1. Use one-liners: lcm = lambda a, b: a*b // math.gcd(a, b)
  2. Precompute for small numbers: Create lookup tables for frequently used ranges
  3. Fast I/O: Use sys.stdin.readline() for faster input
  4. Avoid unnecessary calculations: Check if numbers are coprime (GCD = 1)
  5. Use built-ins when possible: math.lcm() in Python 3.9+
# Competitive programming template import math from sys import stdin input = stdin.readline lcm = lambda a, b: a*b // math.gcd(a, b) t = int(input()) for _ in range(t): a, b = map(int, input().split()) print(lcm(a, b))

External Resources for Further Learning

Official Python Documentation

Related Python Tutorials on EmitechLogic

Advanced Learning Resources

Congratulations! You’ve Mastered Python LCM

You now know 4 different methods to calculate LCM in Python, from basic while loops to advanced competitive programming techniques.

Next steps: Practice with the interactive calculator, try the quiz, and implement these methods in your own projects!

Related posts:

Python Garbage Collection: How to Optimize Performance

The Ultimate Guide to Python Data Types (Part 1)

Python id() Function Explained: How Memory Addressing Works

AI in Cybersecurity: How Artificial Intelligence is Redefining Security in 2025

About The Author

Emmimal Alexander

Emmimal Alexander is an AI & Machine Learning Expert, passionate educator, and the author of “Neural Networks and Deep Learning with Python.” As the founder of EmiTechLogic, she’s on a mission to make complex tech topics accessible, engaging, and empowering for learners at every level.

With deep expertise in Python, HTML, JavaScript, and CSS, Emmimal brings a strong coding foundation to her tutorials and educational resources. Her work focuses on blending theoretical understanding with real-world application—so readers not only learn how things work, but also why they matter.

Through EmiTechLogic, she creates hands-on guides, detailed breakdowns, and project-based learning content that bridges the gap between academic concepts and practical implementation. Whether you’re exploring AI for the first time or fine-tuning your neural networks, you’re in the right place.

See author's posts

Tags:

Leave a Reply

Your email address will not be published. Required fields are marked *

  • Rating