Top 50 Data Science Interview Questions | Part-1
Introduction
Are you gearing up for a data science interview at a leading tech company? If so, you’re in the right place! The world of data science is exciting and ever-evolving, but it can also be daunting when preparing for Data Science Interview Questions. With so many companies seeking skilled professionals who can analyze data, draw insights, and make informed decisions, having the right preparation can make all the difference.
In this blog post, we’ve compiled the Top 100 Data Science Interview Questions & Answers for 2024 that you’re likely to encounter. These questions have been carefully selected based on feedback from recent candidates at some of the most prestigious tech companies. Whether you’re a professional or just starting your journey in data science, these questions cover a wide range of topics, from statistics and machine learning to data manipulation and programming skills.
We know that interviews can be nerve-wracking, so we’ve aimed to make this resource as helpful and approachable as possible. Each question is followed by a clear and concise answer, giving you insights into what interviewers are really looking for. Our goal is not only to help you prepare but also to boost your confidence as you head into your next interview.
So, grab a cup of coffee, get comfortable, and let’s dive into the world of data science interviews! By the end of this blog post, you’ll feel more prepared to tackle those tough questions and showcase your skills effectively. Let’s get started!
General Data Science Questions
1. What is Data Science, and How is it Different from Data Analysis?
Data Science is an interdisciplinary field that combines techniques from statistics, mathematics, computer science, and domain knowledge to extract insights and knowledge from structured and unstructured data. It involves a comprehensive process that includes data collection, cleaning, analysis, and interpretation, ultimately leading to informed decision-making. Data scientists use various tools and algorithms to model data, predict future trends, and uncover patterns that can drive strategic business actions.
On the other hand, Data Analysis is a subset of Data Science that focuses specifically on analyzing data to extract meaningful insights. It involves interpreting existing data to answer specific questions or solve particular problems. Data analysts often use statistical tools to summarize and visualize data, providing reports or dashboards that highlight key findings.
In summary, while data analysis is a crucial part of the broader data science process, data science encompasses a wider range of activities. Data scientists not only analyze data but also develop models, build algorithms, and apply machine learning techniques to predict outcomes and generate insights, often working on more complex and diverse data challenges.
2. Explain the data science project lifecycle
The data science project lifecycle is a series of steps that guide data scientists through a project from start The data science project lifecycle consists of several stages that help data scientists work through a project from start to finish. Understanding this lifecycle is important for successfully completing a data science project. Here’s a simple breakdown of each stage:
1. Problem Definition
First, you need to understand the problem you want to solve. This step involves talking to stakeholders and identifying their needs. Make sure you know the project goals and what success looks like.
2. Data Collection
Once you define the problem, the next step is to gather the data. You can collect data from various sources, such as databases, APIs, or web scraping. The more relevant data you have, the better your analysis will be.
3. Data Cleaning
After collecting the data, it’s time to clean it. This step involves removing duplicates, fixing errors, and handling missing values. Clean data is crucial because it ensures your analysis is accurate.
4. Exploratory Data Analysis (EDA)
Next, you perform exploratory data analysis. This step helps you understand the data better. You can use visualizations and statistics to uncover patterns and relationships. EDA provides valuable insights that guide your next steps.
5. Feature Engineering
In this stage, you create new features from your existing data. Features are the inputs used in your models. Good feature engineering can improve model performance. Think of it as preparing the data to get the best results.
6. Model Building
Now it’s time to build your model. You choose the right algorithm based on the problem type and the data you have. This can involve using machine learning techniques like regression, classification, or clustering. You’ll also split the data into training and testing sets to evaluate your model.
7. Model Evaluation
After building the model, you evaluate its performance. You use metrics like accuracy, precision, and recall to see how well it works. If the results aren’t satisfactory, you may need to go back and tweak your model or try different features.
8. Deployment
Once you have a good model, the next step is deployment. This means putting your model into production so others can use it. You’ll need to ensure it works well in a real-world setting and is accessible to users.
9. Monitoring and Maintenance
After deployment, it’s important to monitor the model’s performance over time. Data and conditions can change, so you may need to update the model regularly. This step ensures that it continues to provide accurate predictions.
In summary, the data science project lifecycle includes defining the problem, collecting and cleaning data, analyzing it, building and evaluating models, deploying them, and monitoring their performance. Understanding each stage helps you manage a data science project effectively and achieve your goals.
3. What are the key steps in the data preprocessing phase?
Data preprocessing is an important step in any data science project. It prepares the data for analysis and helps ensure good results. Here are the key steps in the data preprocessing phase:
1. Data Collection
First, gather all the relevant data you need for your project. This data can come from various sources, like databases, spreadsheets, or APIs. Make sure you collect enough data to work with.
2. Data Cleaning
Next, clean the data. This step is crucial because real-world data often has errors. Look for missing values, duplicates, and outliers. Remove or fix these issues to ensure your data is accurate and reliable.
3. Data Transformation
After cleaning, transform the data to fit your analysis needs. This might involve changing data types, normalizing values, or scaling features. For example, if you have numerical data on different scales, you may want to normalize it so that they are on a similar scale.
4. Feature Selection
In this step, choose the most important features for your analysis. Not all data features will be relevant, so it’s essential to select those that will help your model perform better. You can use techniques like correlation analysis or feature importance scores to guide your choices.
5. Feature Engineering
Feature engineering involves creating new features from your existing data. This can help improve model performance. For example, you might combine two features into one or extract information from a date feature, like the day of the week.
6. Data Splitting
Before building your model, split the data into training and testing sets. The training set is used to train your model, while the testing set evaluates its performance. A common split is 80% for training and 20% for testing.
7. Encoding Categorical Variables
If you have categorical data, you’ll need to convert it into a numerical format. This can be done using techniques like one-hot encoding or label encoding. This step is necessary because most machine learning algorithms work with numbers.
In summary, the key steps in the data preprocessing phase include collecting data, cleaning it, transforming it, selecting and engineering features, splitting the data, and encoding categorical variables. These steps are essential for preparing your data for analysis and ensuring your models work well.
4. Describe the importance of feature selection.
Feature selection is an essential part of the data science process. It involves choosing the most relevant features from your dataset for model training. Here’s why it’s so important:
- Improves Accuracy
Selecting the right features helps your model focus on the most important information. This can lead to better predictions and higher accuracy. - Reduces Overfitting
Using too many features can make your model too complex. This can cause it to learn noise instead of real patterns in the data. Feature selection helps prevent overfitting, making your model work better with new data. - Saves Time and Resources
A model with fewer features trains faster and is easier to work with. This can save time during development and lower computational costs. - Enhances Interpretability
When your model has fewer features, it’s easier to understand. This can help stakeholders see which features are most important and why, leading to better decision-making. - Improves Data Quality
The process of selecting features encourages you to examine your data closely. This can reveal any quality issues, like irrelevant or duplicate features, that need to be addressed. - Reduces Multicollinearity
Sometimes, features can be highly correlated with one another. This can confuse your model and affect its performance. By carefully selecting features, you can minimize multicollinearity and improve the stability of your model.
In short, feature selection is crucial because it improves accuracy, reduces overfitting, saves time, enhances interpretability, improves data quality, and reduces multicollinearity.
5. What is the difference between supervised and unsupervised learning?
The difference between supervised and unsupervised learning mainly lies in how they use data.
In supervised learning, we train the model on labeled data. This means we have input-output pairs where the outcome is known. The goal is to predict outcomes for new data. For example, we might classify emails as spam or not spam.
On the other hand, unsupervised learning works with unlabeled data. Here, we don’t know the outcomes. The goal is to find patterns or groupings within the data. A common use case is customer segmentation based on purchasing behavior.
So, in short, supervised learning is about predicting known outcomes, while unsupervised learning is about discovering patterns in data without known labels.
6. What is overfitting, and how can you prevent it?
Overfitting occurs when a machine learning model learns the training data too well, capturing noise and outliers instead of the underlying pattern. As a result, the model performs well on the training data but poorly on unseen data, meaning it doesn’t generalize effectively.
To prevent overfitting, you can use several techniques:
- Train with More Data: Providing more training examples can help the model learn better general patterns instead of memorizing the training data.
- Simplify the Model: Use a less complex model with fewer parameters. This reduces the chance of capturing noise.
- Regularization: Techniques like L1 (Lasso) and L2 (Ridge) regularization add a penalty for larger coefficients in the model. This encourages simpler models and helps prevent overfitting.
- Cross-Validation: Use techniques like k-fold cross-validation to evaluate your model’s performance. This ensures that the model performs well across different subsets of the data.
- Early Stopping: Monitor the model’s performance on a validation set during training. Stop training when performance on the validation set starts to degrade.
- Data Augmentation: For tasks like image classification, augmenting the training data by creating variations (like rotating or flipping images) can help improve generalization.
By applying these techniques, you can reduce the risk of overfitting and create a model that performs better on unseen data.
7. Explain the concept of bias-variance tradeoff.
The bias-variance tradeoff is a key idea in machine learning. It helps us understand errors in our models.
- Bias: This is the error from using a simplified model to represent a complex problem. High bias means the model makes strong assumptions and may miss important patterns. For example, using a straight line to fit a curve leads to high bias.
- Variance: This refers to how much the model changes with small changes in the training data. High variance means the model learns the training data too well, including its noise. This can lead to overfitting. For instance, a complex model with many parameters might fit the training data perfectly but fail on new data.
The tradeoff is about balancing bias and variance. A model with low bias and high variance fits the training data well but struggles with new data. In contrast, a model with high bias and low variance may not capture the data patterns, leading to underfitting.
Our goal is to minimize total error, which includes bias, variance, and irreducible error (the noise in the data). We want to find a model complexity that generalizes well. By understanding this tradeoff, we can make better choices when developing and tuning machine learning models.
8. What is the difference between classification and regression?
Classification and regression are both types of supervised learning, but they serve different purposes.
Classification is used to categorize data into distinct classes. The output is a discrete label. For example, classifying an email as “spam” or “not spam.” Other examples include image recognition, where we identify objects, or diagnosing diseases based on symptoms.
Regression, on the other hand, is used to predict continuous numerical values. The output is a number. For instance, predicting the price of a house based on its features, like size and location. Other examples include forecasting sales or estimating a person’s weight based on height.
So, in short, classification deals with discrete categories, while regression focuses on predicting continuous values.
9. What are some common metrics used to evaluate model performance?
There are several key metrics used to evaluate model performance, depending on whether you’re working with classification or regression tasks.
For Classification:
- Accuracy: This measures the percentage of correctly predicted instances out of the total instances. It’s simple but can be misleading if the classes are imbalanced.
- Precision: This indicates how many of the predicted positive instances are actually positive. It helps assess the quality of the positive predictions.
- Recall (Sensitivity): This measures how many actual positive instances were correctly predicted. It shows how well the model captures positive cases.
- F1 Score: This is the harmonic mean of precision and recall. It provides a balance between the two and is useful when you need a single metric to evaluate the model.
- ROC-AUC (Receiver Operating Characteristic – Area Under Curve): This evaluates the model’s ability to distinguish between classes. A higher AUC value indicates better performance.
For Regression:
- Mean Absolute Error (MAE): This measures the average absolute difference between predicted and actual values. It provides a straightforward way to understand the model’s error.
- Mean Squared Error (MSE): This calculates the average of the squared differences between predicted and actual values. It gives more weight to larger errors, which can be helpful in some contexts.
- Root Mean Squared Error (RMSE): This is the square root of the MSE. It brings the error back to the same scale as the original values, making it easier to interpret.
- R-squared (Coefficient of Determination): This indicates how well the independent variables explain the variability of the dependent variable. A higher R-squared value means a better fit.
In summary, the choice of metrics depends on the specific problem you’re addressing, whether it’s classification or regression. Each metric provides different insights into model performance.
10. How do you handle missing data in a dataset?
Handling missing data is crucial for building effective models. Here are some common strategies I use:
- Remove Missing Data: If the amount of missing data is small, I might choose to remove those rows or columns. This approach works well when the missing values won’t significantly impact the analysis.
- Imputation: For missing values, I often use imputation techniques. This involves filling in missing data with estimates:
- Mean/Median Imputation: For numerical features, I can replace missing values with the mean or median of that column.
- Mode Imputation: For categorical features, I can fill in missing values with the most frequent category.
- K-Nearest Neighbors (KNN): This method uses the values from the closest data points to estimate missing values.
- Predictive Modeling: Sometimes, I use regression or other machine learning algorithms to predict and fill in missing values based on other features in the dataset.
- Flagging Missing Values: I may create an additional binary feature that indicates whether a value was missing. This can provide the model with useful information about the data.
- Leave as Missing: In some cases, it might be acceptable to leave values as missing, especially if the model can handle them, like tree-based algorithms.
Choosing the right method depends on the amount of missing data, the nature of the dataset, and the potential impact on the analysis. It’s essential to carefully assess the situation to ensure the integrity of the model.
Must Read
- Why sorted() Is Safer Than list.sort() in Production Python Systems
- Monotonic Sequence in Python: 7 Practical Methods With Edge Cases, Interview Tips, and Performance Analysis
- How to Check if Dictionary Values Are Sorted in Python
- Check If a Tuple Is Sorted in Python — 5 Methods Explained
- How to Check If a List Is Sorted in Python (Without Using sort()) – 5 Efficient Methods
Statistics and Probability
11. What is the Central Limit Theorem?
The Central Limit Theorem (CLT) is a fundamental concept in statistics. It states that when you take a large enough sample size from a population, the distribution of the sample means will approach a normal distribution, regardless of the original population’s distribution.
Here are the key points:
- Sample Means: If you repeatedly take samples of a certain size from any population and calculate their means, those means will form a new distribution.
- Normal Distribution: As the sample size increases, this distribution of sample means will become more and more like a normal distribution (bell-shaped curve), even if the original population is not normally distributed.
- Sample Size: A common rule of thumb is that a sample size of 30 or more is usually sufficient for the CLT to hold, but larger samples are better.
- Mean and Standard Deviation: The mean of the sample means will be equal to the population mean, while the standard deviation of the sample means (also known as the standard error) will equal the population standard deviation divided by the square root of the sample size.
The CLT is crucial because it allows us to make inferences about population parameters using sample data, which is a foundational aspect of hypothesis testing and confidence intervals in statistics. It essentially enables us to apply statistical methods that assume normality, even when working with non-normally distributed populations.
12. Explain the difference between Type I and Type II errors
Type I and Type II errors are concepts in hypothesis testing that relate to incorrect conclusions drawn from statistical tests.
- Type I Error (False Positive):
- This error occurs when we reject the null hypothesis (the default assumption) when it is actually true.
- In simpler terms, it’s like saying something significant is happening when, in reality, it is not.
- For example, if a new drug is claimed to be effective when it actually has no effect, that would be a Type I error.
- The probability of making a Type I error is denoted by alpha (α), often set at 0.05. This means we accept a 5% chance of making this error.
- Type II Error (False Negative):
- This error occurs when we fail to reject the null hypothesis when it is actually false.
- Essentially, it means saying nothing significant is happening when there is, in fact, an effect or difference.
- For instance, if a test shows that a drug is ineffective when it really works, that’s a Type II error.
- The probability of making a Type II error is denoted by beta (β).
In summary, a Type I error is about detecting an effect that isn’t there, while a Type II error is about missing an effect that is there. Understanding these errors helps in making informed decisions about significance levels and the trade-offs involved in hypothesis testing.
13. What is p-value, and what does it signify?
A p-value is a statistical measure that helps us determine the significance of our results in hypothesis testing. It quantifies the probability of obtaining results at least as extreme as the observed results, assuming that the null hypothesis is true.
Here’s what it signifies:
- Null Hypothesis: The p-value is based on the null hypothesis, which is a statement that there is no effect or no difference in the population.
- Interpretation:
- A low p-value (typically ≤ 0.05) suggests that the observed data is unlikely under the null hypothesis. This leads us to reject the null hypothesis, indicating that there is evidence for an effect or a difference.
- A high p-value (> 0.05) indicates that the observed data is consistent with the null hypothesis. This means we do not have enough evidence to reject it.
- Context Matters: It’s important to remember that a p-value does not measure the size or importance of an effect. It only tells us about the evidence against the null hypothesis. For example, a small p-value might indicate a statistically significant result, but the practical significance could be negligible.
- Limitations: P-values can be influenced by sample size. Larger samples can produce smaller p-values, even for trivial effects. Therefore, it’s essential to consider other factors, such as effect size and confidence intervals, alongside p-values when making conclusions.
In summary, the p-value helps us assess the strength of the evidence against the null hypothesis. It plays a crucial role in determining whether we accept or reject that hypothesis in our statistical analyses.
14. Describe the difference between parametric and non-parametric tests
Parametric and non-parametric tests are two broad categories of statistical tests used to analyze data, and they have distinct characteristics and applications.
Parametric Tests:
- Assumptions: Parametric tests assume that the data follows a specific distribution, usually a normal distribution. They also often assume homogeneity of variance and that the data is measured at an interval or ratio scale.
- Examples: Common parametric tests include:
- t-tests: For comparing means between two groups.
- ANOVA (Analysis of Variance): For comparing means among three or more groups.
- Pearson’s correlation: For measuring the strength and direction of a linear relationship between two continuous variables.
- Advantages:
- They are generally more powerful than non-parametric tests when their assumptions are met, meaning they are more likely to detect a true effect when one exists.
- They can provide more precise estimates, as they take into account the distribution of the data.
Non-Parametric Tests:
- Assumptions: Non-parametric tests do not assume a specific distribution for the data. They can be used with ordinal data or when the data does not meet the assumptions required for parametric tests.
- Examples: Common non-parametric tests include:
- Mann-Whitney U test: For comparing two independent groups when the data does not follow a normal distribution.
- Wilcoxon signed-rank test: For comparing two related groups.
- Kruskal-Wallis test: For comparing three or more independent groups.
- Advantages:
- They are more flexible because they do not require data to meet strict assumptions.
- They can be used with small sample sizes or non-normally distributed data.
In summary, the key difference lies in the assumptions about the data. Parametric tests require the data to meet certain conditions and are more powerful under those conditions. Non-parametric tests are more versatile and can be used in a wider range of situations, but they may be less powerful when parametric assumptions are satisfied. Choosing between the two depends on the nature of your data and the specific hypotheses being tested.
15. Explain the concept of confidence intervals
Confidence intervals (CIs) are a statistical tool used to estimate a range in which a population parameter, like a mean or proportion, likely falls. They help us understand the uncertainty around our sample estimates. Here’s a simple overview:
- Purpose: The main purpose of a confidence interval is to give us a range around a sample statistic, indicating how confident we are that the true population parameter is within that range.
- Components: A confidence interval consists of a point estimate, which is the value we get from our sample data (like the sample mean), and a margin of error, which shows the uncertainty around that estimate.
- Confidence Level: The confidence level tells us how likely it is that the confidence interval contains the true parameter. Common levels are 90%, 95%, and 99%. For example, if we say we have a 95% confidence interval, it means that if we took many samples and calculated a CI for each, about 95% of those intervals would include the true population mean.
- Calculation: The formula for a confidence interval is:
The critical value depends on the chosen confidence level, and the standard error measures the variability of our sample.
Interpretation: If we calculate a 95% confidence interval of (50, 60) for the average height of a population, it means we are 95% confident that the true average height falls between 50 and 60. However, it doesn’t guarantee that the true average is in that range for any single sample.
In summary, confidence intervals are essential for expressing the uncertainty of our estimates and help guide decision-making based on statistical data.
16. What is A/B testing, and how do you conduct it?
A/B testing, or split testing, is a method used to compare two versions of something to see which one performs better. It’s widely used in marketing and product development to make data-driven decisions. Here’s how it works:
- Define Your Objective: Start by deciding what you want to test, like increasing click-through rates or improving conversion rates.
- Choose the Variable: Select the specific element you want to test, such as a headline, button color, or layout.
- Create Variants: Develop two versions: the original (A) and the modified version (B). The only difference between them should be the variable you are testing.
- Randomly Assign Participants: Split your audience randomly into two groups. Group A sees version A, and Group B sees version B. This helps ensure unbiased results.
- Run the Test: Launch both versions at the same time. Make sure to run the test long enough to gather meaningful data, depending on your audience size.
- Analyze Results: Once the test is complete, compare the performance of both versions based on your objective. Look for statistically significant differences.
- Draw Conclusions: Decide which version performed better and implement the winning version.
- Iterate: A/B testing is ongoing. Use insights from each test to inform future tests and optimize your approach continuously.
In summary, A/B testing is a valuable tool for optimizing products and marketing strategies based on real user data. It allows businesses to make informed decisions and enhance user experiences effectively.
17. What are common distributions used in statistics?
There are several common distributions used in statistics, each with unique properties and applications. Here are some of the most widely used ones:
1. Normal Distribution:
- This is perhaps the most well-known distribution. It is symmetric and bell-shaped, characterized by its mean and standard deviation.
- Many statistical methods assume normality, making it crucial in inferential statistics.
Examples include heights of people and test scores.
2. Binomial Distribution:
- This distribution models the number of successes in a fixed number of independent Bernoulli trials (yes/no experiments).
- It is defined by two parameters: the number of trials (n) and the probability of success (p).
Common examples include flipping a coin a certain number of times or determining the number of successful sales calls in a day.
3. Poisson Distribution:
- The Poisson distribution is used for counting the number of events that occur in a fixed interval of time or space.
- It is characterized by its rate parameter (λ), which represents the average number of events in the interval.
Examples include the number of emails received in an hour or the number of cars passing a checkpoint in a day.
4. Exponential Distribution:
- This distribution models the time until the next event occurs in a Poisson process.
- It is often used to describe waiting times, such as the time between arrivals of customers at a store.
The exponential distribution has a single parameter (λ), which is the rate of the event.
5. Uniform Distribution:
- In a uniform distribution, all outcomes are equally likely within a certain range.
- This can be either discrete (e.g., rolling a fair die) or continuous (e.g., choosing a random number between 0 and 1).
- It is useful in simulations and modeling scenarios where each outcome is equally probable.
6. T-distribution:
- The t-distribution is similar to the normal distribution but has heavier tails. It is used when the sample size is small and the population standard deviation is unknown.
- It is often used in hypothesis testing and confidence intervals for small samples.
7. Chi-Squared Distribution:
- This distribution is used primarily in hypothesis testing, particularly for tests of independence and goodness of fit.
- It is based on the sum of the squares of independent standard normal variables.
In summary, these distributions are foundational in statistics and are used in various applications. Understanding these common distributions helps in selecting the right statistical methods and interpreting data accurately.
18. How do you calculate the correlation coefficient?
The correlation coefficient measures the strength and direction of a linear relationship between two variables. The most common type is the Pearson correlation coefficient, denoted as r. Here’s how to calculate it:
- Collect Your Data: Gather paired data for the two variables you want to analyze. For example, let’s say you have two variables, X and Y.
- Calculate the Means: Find the mean (average) of each variable.

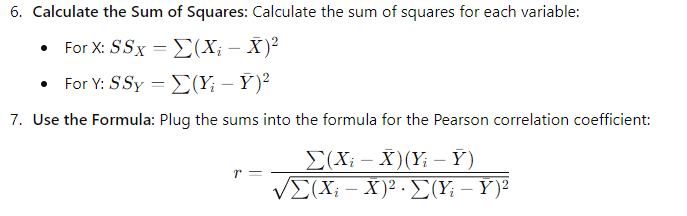
8. Interpret the Result:
A value of 1 indicates a perfect positive correlation, meaning that as one variable increases, the other does as well. Conversely, a value of -1 signifies a perfect negative correlation, indicating that as one variable increases, the other decreases. Finally, a value of 0 suggests no correlation exists between the variables.
In summary, calculating the correlation coefficient involves collecting data, calculating means, finding deviations, and applying a formula. This process helps quantify the relationship between two variables, guiding decisions based on the strength and direction of that relationship.
19. What is hypothesis testing?
Hypothesis testing is a statistical method used to make decisions or inferences about a population based on sample data. It helps us determine whether there is enough evidence to support a specific claim or hypothesis. Here’s a straightforward overview:
1. Formulating Hypotheses:
We start with two competing hypotheses:
- Null Hypothesis (H₀): This is the default statement that there is no effect or no difference. It represents the status quo.
- Alternative Hypothesis (H₁ or Ha): This is what we want to prove. It suggests that there is an effect or a difference.
2. Choosing a Significance Level (α):
This is the threshold for deciding whether to reject the null hypothesis. A common choice is 0.05 (5%). This means we’re willing to accept a 5% chance of incorrectly rejecting the null hypothesis.
3. Collecting Data:
We gather data from a sample of the population. The sample should be random and representative to ensure reliable results.
4. Calculating a Test Statistic:
Based on the sample data, we calculate a test statistic (like a z-score or t-score). This statistic quantifies how far our sample statistic is from the null hypothesis.
5. Determining the P-Value:
The p-value indicates the probability of observing our test statistic (or something more extreme) if the null hypothesis is true. A low p-value suggests that our sample provides strong evidence against the null hypothesis.
6. Making a Decision:
If the p-value is less than or equal to the significance level (α), we reject the null hypothesis. This indicates that our sample provides sufficient evidence to support the alternative hypothesis.
If the p-value is greater than α, we fail to reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.
7. Drawing Conclusions:
Finally, we interpret the results in the context of the original research question. We communicate whether we found evidence to support our hypothesis and the implications of that evidence.
In summary, hypothesis testing is a structured approach to making decisions based on sample data. It allows researchers to assess evidence against a claim and helps inform decisions in various fields, including science, medicine, and business.
20. Explain Bayes’ Theorem with an example
Bayes’ Theorem is a fundamental concept in probability and statistics that describes how to update the probability of a hypothesis based on new evidence. It relates the conditional and marginal probabilities of random events. The theorem can be expressed with the formula:

Example:
Let’s use a medical example to illustrate Bayes’ Theorem:
Scenario: Suppose there’s a rare disease that affects 1% of a population. There’s a test for this disease that is 90% accurate, meaning:
- If a person has the disease, the test will correctly identify it 90% of the time (true positive).
- If a person does not have the disease, the test will correctly identify that they don’t have it 90% of the time (true negative).

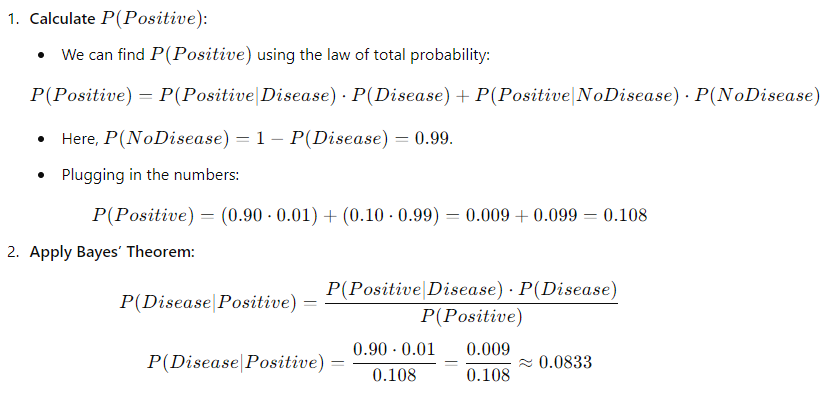
This means that even after receiving a positive test result, there is only about an 8.33% chance that the person actually has the disease. This example illustrates how Bayes’ Theorem helps update our belief about the probability of having the disease based on the test result, showing the importance of considering the base rate of the disease and the accuracy of the test.
Machine Learning
21. What is the difference between decision trees and random forests?
Decision trees and random forests are both popular machine learning algorithms used for classification and regression tasks, but they have some key differences:
Decision Trees:
- Structure: A decision tree is a flowchart-like model that splits data into branches based on feature values. Each node represents a feature, and each branch represents a decision rule. The leaves represent the final outcomes.
- Simplicity: Decision trees are straightforward and easy to interpret. You can visualize the decisions made at each node, making it simple to understand how the model reaches a conclusion.
- Overfitting: Decision trees can easily overfit the training data, especially if they are deep. This means they may perform well on training data but poorly on unseen data because they capture noise instead of the underlying pattern.
- Sensitivity to Data: They are sensitive to small changes in the data, which can lead to completely different trees.
Random Forests:
- Ensemble Method: A random forest is an ensemble method that creates multiple decision trees and combines their predictions. Each tree is built using a random subset of the training data and a random selection of features.
- Robustness: Random forests are more stronger than individual decision trees. By averaging the predictions from multiple trees, they reduce the risk of overfitting and increase generalization performance on unseen data.
- Feature Importance: Random forests can provide insights into feature importance. By analyzing how much each feature contributes to the overall predictions across all trees, you can identify which features are most influential.
- Less Interpretable: While random forests improve accuracy, they are less interpretable than single decision trees. Understanding the specific decision-making process becomes more complex because it involves many trees.
In summary, decision trees are simple, interpretable models that can easily overfit the data, while random forests are collections of decision trees that enhance performance and robustness by averaging their predictions. Random forests often yield better accuracy and generalization, especially in complex datasets, but at the cost of some interpretability.
22. Explain how support vector machines (SVM) work
Support Vector Machines (SVM) are supervised learning models used for classification and regression. Here’s how they work:
- Finding the Hyperplane: SVM aims to find a hyperplane that best separates different classes in the data. In two dimensions, this hyperplane is simply a line, while in three dimensions, it’s a plane. The goal is to maximize the margin, which is the distance between the hyperplane and the nearest data points from each class.
- Support Vectors: The data points that are closest to the hyperplane are called support vectors. These points are crucial because they determine the position and orientation of the hyperplane. If we remove any other data points, the hyperplane will not change.
- Maximizing the Margin: SVM tries to maximize the margin between the support vectors of each class. A larger margin helps improve the model’s generalization to unseen data, which is important for effective classification.
- Kernel Trick: If the data is not linearly separable (i.e., you can’t draw a straight line to separate the classes), SVM uses a technique called the kernel trick. This transforms the data into a higher-dimensional space where a hyperplane can effectively separate the classes. Common kernels include linear, polynomial, and radial basis function (RBF).
- Classification: Once the hyperplane is established, SVM can classify new data points by determining which side of the hyperplane they fall on. If a point is on one side, it belongs to one class; if it’s on the other, it belongs to another class.
In essence, SVM is a powerful tool for classification. It finds the optimal hyperplane that separates classes by maximizing the margin, and with the help of kernel functions, it can handle complex, non-linear relationships. This makes SVM suitable for a wide range of applications, especially in high-dimensional spaces.
23. What is k-fold cross-validation?
K-fold cross-validation is a method used to evaluate how well a machine learning model performs. It helps ensure that the model will work well on new, unseen data. Here’s a simple way to understand it:
- Splitting the Data: First, you divide your dataset into k equal parts, called “folds.” For example, if you have 100 data points and you choose k = 5, you’ll have five groups of 20 data points each.
- Training and Testing: Next, you train your model k times. Each time, you use k-1 folds to train the model and the remaining fold to test it. This way, every fold gets to be the test set once.
- Evaluating Performance: After running through all the folds, you’ll end up with k different performance scores. These scores could be things like accuracy or F1 score, depending on what you’re measuring.
- Averaging the Scores: Finally, you take the average of these k scores to get a single performance metric for your model. This average gives you a better idea of how the model will perform on new data compared to just using one train-test split.
Why Use K-Fold Cross-Validation?
- Reliable Evaluation: It gives a more trustworthy estimate of your model’s performance because it uses multiple ways to test it. This reduces the chance of getting a misleading result from just one split.
- Better Data Usage: You get to use all your data for both training and testing. This is especially helpful if you have a small dataset.
Choosing the Right k:
- A common choice for k is 5 or 10. Choosing a larger k gives a more reliable estimate but may take more time to compute.
In short, k-fold cross-validation is a smart way to check how well your model is likely to perform on new data. It helps you build a model that is not just good on the training data but also generalizes well to unseen cases.
24. Describe the working of a neural network
A neural network is a system that mimics how our brains work to process information. Here’s a straightforward way to understand how it operates:
1. Structure:
A neural network is made up of layers of nodes, or neurons. It generally has three types of layers:
- Input Layer: This is where the network receives the data. Each node in this layer represents a different feature of the input.
- Hidden Layers: These are the layers between the input and output layers. There can be several hidden layers, and each one contains multiple neurons. This is where the real processing happens.
- Output Layer: This layer produces the final output or prediction of the network.
2. Forward Propagation:
When data enters the network, it flows through these layers one by one. Each neuron in the hidden layers takes input from the neurons of the previous layer. It applies a weight to that input, adds a bias, and then passes the result through an activation function, which adds non-linearity to the model. This step helps the network learn complex patterns in the data.
3. Weights and Biases:
Each connection between neurons has a weight that controls how much influence one neuron has on another. Biases are added to help the network adjust the output. During training, the network learns by tweaking these weights and biases based on the data it sees.
4. Loss Function:
After the output is generated, the network compares it to the actual target value using a loss function. This function measures how far the network’s prediction is from the correct answer. For example, mean squared error is often used for regression tasks, while cross-entropy loss is common for classification.
5.Backpropagation:
The network then adjusts the weights and biases to minimize the loss. This process, called backpropagation, calculates how much each weight contributed to the error and updates them accordingly. It uses techniques like stochastic gradient descent or Adam to do this efficiently.
6. Training:
This process of forward propagation and backpropagation is repeated multiple times using different batches of data. With each pass, the network improves its predictions by fine-tuning its parameters.
In summary, a neural network processes data through layers of interconnected neurons. It learns to make predictions by adjusting weights and biases based on how well it performs. Over time, through training, the network gets better at recognizing patterns and making accurate predictions.
25. What are hyperparameters, and how do you tune them?
Hyperparameters are settings that you can configure before training a machine learning model. Unlike regular parameters, which the model learns during training, hyperparameters are set manually. They play a crucial role in determining how well your model performs. Here’s how they work:
1. Examples of Hyperparameters:
Common hyperparameters include:
- Learning Rate: This controls how much the model adjusts its weights during training. A high learning rate can cause the model to miss the best solution, while a low rate can make training too slow.
- Number of Hidden Layers and Neurons: In a neural network, you decide how many hidden layers and how many neurons in each layer. This affects the model’s capacity to learn.
- Batch Size: This is the number of training samples used in one iteration. Smaller batch sizes can provide a more accurate estimate of the gradient but take longer to train.
- Regularization Parameters: These help prevent overfitting by adding a penalty for large weights.
2. Tuning Hyperparameters:
Tuning hyperparameters involves finding the best combination of these settings to improve model performance. Here are some common methods for tuning:
- Grid Search: This method involves specifying a set of hyperparameters and their possible values. The model is trained and evaluated for every combination, which can be time-consuming but thorough.
- Random Search: Instead of trying all combinations, this method randomly samples from the hyperparameter space. It’s often more efficient than grid search.
- Bayesian Optimization: This is a more advanced technique that builds a probabilistic model of the function that maps hyperparameters to the model’s performance. It helps to explore the hyperparameter space more intelligently.
- Cross-Validation: When tuning hyperparameters, it’s essential to evaluate model performance using techniques like k-fold cross-validation. This helps ensure that the model generalizes well to unseen data.
3. Automated Tuning Tools:
There are also automated tools available, like Optuna or Hyperopt, which can help streamline the hyperparameter tuning process.
In short, hyperparameters are key settings you choose before training a model. Tuning them is crucial for optimizing model performance. Methods like grid search, random search, and Bayesian optimization can help find the best values for these hyperparameters.
26. Explain the concept of ensemble learning
Ensemble learning is a technique in machine learning where multiple models, or learners, are combined to improve the overall performance of a predictive model. The idea is simple: by bringing together different models, you can leverage their strengths and minimize their weaknesses. Here’s how it works:
Why Use Ensemble Learning?
Individual models might make different predictions based on the data they are trained on. Some models may perform well in certain situations but poorly in others. By combining their predictions, you can often achieve better accuracy and robustness.
Types of Ensemble Learning Methods:
Bagging (Bootstrap Aggregating): This method involves training multiple models on different subsets of the training data. Each subset is created by sampling with replacement. The final prediction is made by averaging the predictions (for regression) or by voting (for classification) from all models. A popular example of bagging is the Random Forest algorithm.
Boosting: In boosting, models are trained sequentially. Each new model focuses on the errors made by the previous models. The idea is to give more weight to the misclassified instances so that the new model learns from those mistakes. Examples of boosting algorithms include AdaBoost, Gradient Boosting, and XGBoost.
Stacking: This technique involves training multiple models and then combining their predictions using another model, often called a meta-learner. The base models might be different types of algorithms, and the meta-learner learns how to best combine their predictions.
Advantages of Ensemble Learning:
Improved Accuracy: By combining models, ensemble methods can often outperform individual models, especially when the models have diverse predictions.
Robustness: Ensemble models are generally more robust to overfitting because they balance out the errors of individual models.
Versatility: Ensemble learning can be applied to any type of model, whether it’s decision trees, neural networks, or support vector machines.
Considerations:
While ensemble methods can provide better performance, they may also increase complexity. This can lead to longer training times and make interpretation more difficult. It’s essential to weigh these factors when deciding whether to use ensemble methods.
In summary, ensemble learning is about combining multiple models to enhance predictive performance. Techniques like bagging, boosting, and stacking allow us to leverage the strengths of different models and create a more powerful and accurate overall model.
27. What is gradient descent?
Gradient descent is an optimization algorithm used to minimize a function by iteratively moving toward the lowest point, or the minimum. In machine learning, it’s commonly used to update the parameters of a model during training. Here’s a breakdown of how it works:
- Objective: The main goal of gradient descent is to minimize a loss function, which measures how far off a model’s predictions are from the actual values. A lower loss means better performance.
2. Gradient: The gradient is a vector that points in the direction of the steepest increase of a function. In the context of gradient descent, we use the gradient to determine how to adjust the model’s parameters to decrease the loss.
3. Steps of Gradient Descent:
Initialization: Start by initializing the model parameters (like weights) with random values.
Compute the Loss: Calculate the loss using the current model parameters.
Calculate the Gradient: Find the gradient of the loss function with respect to the parameters. This tells you how to change the parameters to reduce the loss.
Update the Parameters: Adjust the parameters by moving them in the opposite direction of the gradient. The size of the step taken is determined by the learning rate, which is a hyperparameter that controls how quickly or slowly the model learns.
Repeat: Repeat the process until the model’s parameters converge to values that minimize the loss function or until a predetermined number of iterations is reached.
4. Types of Gradient Descent:
Batch Gradient Descent: This method uses the entire dataset to compute the gradient and update the parameters. While it’s precise, it can be slow for large datasets.
Stochastic Gradient Descent (SGD): Instead of using the whole dataset, this method updates the parameters using only one training example at a time. This makes it faster and allows for more frequent updates, but the updates can be noisy.
Mini-Batch Gradient Descent: This method is a compromise between batch and stochastic gradient descent. It uses a small random subset of the data (mini-batch) for each update. This can help stabilize the updates while maintaining a faster training speed.
5. Challenges:
Choosing the Learning Rate: If the learning rate is too high, the model may overshoot the minimum. If it’s too low, the training process can become very slow.
Local Minima: Gradient descent can get stuck in local minima, especially in complex loss landscapes. This is why techniques like momentum or using different initialization strategies can be beneficial.
In summary, gradient descent is a key optimization technique used to minimize a loss function in machine learning. By iteratively updating the model parameters based on the gradient of the loss, it helps improve the model’s performance and find the best set of parameters.
28. How do you choose the right algorithm for a given problem?
Choosing the right algorithm for a problem in data science or machine learning involves several steps and considerations. Here’s how I approach it:
1. Understand the Problem Type:
- Classification vs. Regression: Determine whether the problem involves predicting a category (classification) or a continuous value (regression). For instance, if you’re predicting whether an email is spam or not, that’s classification. If you’re predicting house prices, that’s regression.
- Clustering or Anomaly Detection: If your goal is to group similar data points or identify unusual patterns, then clustering or anomaly detection algorithms may be appropriate.
2. Data Characteristics:
- Size of the Dataset: Some algorithms perform well with large datasets (like deep learning models), while others may be more suitable for smaller datasets (like decision trees).
- Feature Types: Consider the types of features in your data (numerical, categorical, or text). For example, linear regression works well with numerical data, while decision trees can handle both numerical and categorical features.
- Missing Values: Some algorithms handle missing values better than others. For instance, tree-based methods can work with missing data, whereas linear regression requires complete datasets.
3. Complexity of the Problem:
- Linearity: If the relationship between features and the target variable is linear, simpler models like linear regression may suffice. For more complex relationships, consider using algorithms like support vector machines or neural networks.
- Interactions: If you believe there are significant interactions between features, tree-based methods or ensemble methods like Random Forest may be beneficial.
4. Performance Considerations:
- Speed: If you need quick predictions or have real-time requirements, simpler models (like logistic regression) are typically faster than complex models (like deep learning).
- Interpretability: If stakeholders need to understand the model’s decisions, simpler and more interpretable models (like decision trees) are often preferred over black-box models (like neural networks).
5. Experimentation and Tuning:
Once I have a few potential algorithms in mind, I implement them and evaluate their performance using metrics like accuracy, precision, recall, or F1-score, depending on the problem type.
I often use techniques like cross-validation to ensure that the results are reliable and not due to overfitting.
6. Iterative Process:
Choosing the right algorithm can be an iterative process. Based on the initial results, I may try different algorithms, tweak hyperparameters, or even combine models (using ensemble methods) to achieve better performance.
In summary, selecting the right algorithm requires understanding the problem type, analyzing data characteristics, considering the complexity of the problem, and evaluating performance. By experimenting with different algorithms and iterating based on results, I can identify the most effective approach for the specific problem at hand.
29. What is deep learning, and how does it differ from traditional machine learning?
Deep learning is a subset of machine learning that focuses on using neural networks with many layers to analyze data. It’s particularly powerful for tasks involving large amounts of unstructured data, such as images, audio, and text. Here’s how it works and how it differs from traditional machine learning:
1. Neural Networks:
- At the core of deep learning are neural networks, which are inspired by the human brain. These networks consist of layers of interconnected nodes (or neurons) that process data. Each layer extracts different features from the input.
- Traditional machine learning models often use simpler algorithms, like linear regression or decision trees, which might require manual feature extraction.
2. Feature Learning:
- In deep learning, the model learns to identify relevant features automatically from raw data. For example, in image recognition, a deep learning model can learn to recognize edges, shapes, and objects without needing specific programming for each feature.
- In contrast, traditional machine learning typically requires domain knowledge to select and engineer features, which can be time-consuming and may not capture all relevant aspects of the data.
3. Data Requirements:
- Deep learning models usually require large amounts of labeled data to train effectively. This is because they have many parameters to optimize, and more data helps improve their performance.
- Traditional machine learning algorithms can perform well with smaller datasets since they are less complex and require fewer parameters.
4. Computational Power:
- Deep learning models are computationally intensive. They often require powerful hardware, such as GPUs, to train within a reasonable time. This allows them to handle the large amounts of data needed for effective learning.
- Traditional machine learning algorithms can often be run on standard computers and may not need as much processing power, making them more accessible for smaller-scale problems.
5. Applications:
- Deep learning has excelled in areas like computer vision (image classification, object detection), natural language processing (translation, sentiment analysis), and speech recognition. Its ability to handle complex patterns makes it a go-to choice for these tasks.
- Traditional machine learning is often applied in scenarios where interpretability is crucial or when the problem can be solved with simpler algorithms, like fraud detection or customer segmentation.
In summary, deep learning is a powerful approach within machine learning that uses complex neural networks to automatically learn features from large amounts of data. It differs from traditional machine learning in terms of architecture, data requirements, computational needs, and application areas. Each approach has its strengths, and the choice between them depends on the specific problem and available resources.
30. Explain the difference between bagging and boosting.
Bagging and boosting are both ensemble techniques used to improve model performance, but they take different approaches.
Bagging, short for Bootstrap Aggregating, aims to reduce variance and prevent overfitting. It does this by training multiple models independently on different random subsets of the training data. These subsets are created by sampling with replacement, so some data points can appear in multiple subsets while others might be left out. The final prediction is made by averaging the outputs of these models for regression or by majority voting for classification.
On the other hand, boosting focuses on reducing both bias and variance. It works by training models sequentially, where each new model is trained to correct the errors of the previous ones. Instead of treating all models equally, boosting gives more weight to the models that perform poorly, so they have a greater influence on the final prediction. This way, the ensemble can focus on the hardest cases to predict.
Common examples of bagging include Random Forests, which combine many decision trees to enhance accuracy. Boosting methods include AdaBoost and Gradient Boosting, known for their strong predictive performance.
In summary, bagging combines multiple models trained independently to reduce variance, while boosting sequentially builds models that learn from previous errors to improve accuracy. Both techniques are powerful but serve different purposes in model development
Programming and Tools
31. Which programming languages are commonly used in data science?
In data science, several programming languages are popular, each serving specific tasks.
First, Python is the most widely used language. Its simplicity makes it easy to learn. Python has a rich set of libraries. For data manipulation, there’s Pandas. For numerical calculations, NumPy is a go-to option. Matplotlib and Seaborn help with data visualization, while Scikit-learn is great for machine learning.
Next, R is another common choice. It excels in statistical analysis and visualization. Many people in academia prefer R. It offers packages like ggplot2 for visualizations and dplyr for data manipulation.
Additionally, SQL (Structured Query Language) is essential for managing databases. Data scientists use SQL to query and manipulate data stored in relational databases. This skill is crucial for effective data retrieval.
Moreover, Julia is gaining popularity. It is efficient for numerical and scientific computing. Julia works well for tasks that require heavy mathematical calculations.
Also, Java plays a role in data science. It is useful for building large-scale applications and often appears in big data frameworks like Apache Hadoop and Apache Spark. This makes it suitable for processing large datasets.
Furthermore, Scala is commonly used with Apache Spark for big data processing. It combines functional and object-oriented programming. This feature allows for concise code and high performance.
Lastly, while not as popular as the others, MATLAB has its place in fields like engineering and finance. It is known for its strong mathematical capabilities and works well for algorithm development and data visualization.
In summary, Python and R dominate data science. SQL is crucial for database management. Each language has its strengths, and the choice often depends on the project’s needs and the data scientist’s familiarity.
32. How do you import libraries in Python?
Importing libraries in Python is simple. You use the import statement. Here’s how it works:
First, if you want to import an entire library, you can simply use:
import library_name
For example, to import the NumPy library, you would write:
import numpy
Next, if you only need specific functions or classes from a library, you can import them directly. Use the following syntax:
from library_name import function_name
For example, if you want to import the array function from NumPy, you can do:
from numpy import array
Additionally, you can give a library or function a different name while importing it. This can make your code cleaner. You can use the as keyword for this. Here’s how:
import library_name as alias
So, for NumPy, you might write:
import numpy as np
Now, you can use np instead of numpy throughout your code.
Finally, remember to install any library before importing it if it’s not included with Python. You can install libraries using pip, like this:
pip install library_name
In summary, importing libraries in Python is easy and flexible. You can import entire libraries, specific functions, or rename them as needed to suit your code.
33. Explain the difference between a list and a tuple in Python
In Python, both lists and tuples are used to store collections of items, but they have key differences.
First, mutability is a major distinction. Lists are mutable, meaning you can change their contents after creation. You can add, remove, or modify items in a list. For example:
my_list = [1, 2, 3]
my_list.append(4) # Now my_list is [1, 2, 3, 4]
On the other hand, tuples are immutable. Once you create a tuple, you cannot change its contents. For instance:
my_tuple = (1, 2, 3)
# Trying to change it will result in an error
# my_tuple[0] = 4 # This will raise a TypeError
Next, the syntax for defining lists and tuples is different. You create a list using square brackets [], like this:
my_list = [1, 2, 3]
For tuples, you use parentheses (), such as:
my_tuple = (1, 2, 3)
Additionally, lists are generally used when you need a collection of items that may change over time. They are great for tasks that require adding or removing items frequently. Conversely, tuples are often used for fixed collections of items. They can also be used as keys in dictionaries because they are hashable, while lists cannot be.
Finally, tuples can be slightly more memory-efficient than lists due to their immutability. This can lead to better performance in certain scenarios.
In summary, lists are mutable and defined with square brackets, while tuples are immutable and defined with parentheses. Choose lists when you need a collection that changes and tuples when you want a fixed collection.
34. How do you handle large datasets in Python?
When handling large datasets in Python, there are several approaches to ensure efficient processing.
First, you can use the Pandas library, which is excellent for data manipulation. However, loading a huge dataset all at once might consume a lot of memory. To handle this, you can read the data in chunks using the chunksize parameter in Pandas:
import pandas as pd
chunks = pd.read_csv('large_dataset.csv', chunksize=10000)
for chunk in chunks:
process(chunk)
This way, you only load part of the dataset into memory at a time.
Next, if the dataset is too large even for chunking, you might consider using Dask. Dask is similar to Pandas but allows parallel computation and works with larger-than-memory datasets:
import dask.dataframe as dd
df = dd.read_csv('large_dataset.csv')
df.head() # Dask uses lazy loading, so it loads data only when necessary
Additionally, when dealing with very large datasets, you can store them in a database and use SQL to query only the required parts. You can use SQLite or connect Python to a database like PostgreSQL or MySQL using the sqlite3 or SQLAlchemy libraries.
import sqlite3
conn = sqlite3.connect('my_database.db')
query = 'SELECT * FROM large_table LIMIT 10000'
df = pd.read_sql(query, conn)
Finally, for really massive datasets, using PySpark or Hadoop can help with distributed computing across many machines. PySpark allows you to process large data in parallel, making it faster and more memory-efficient.
In summary, to handle large datasets in Python, you can use techniques like chunking with Pandas, employing Dask for parallel computing, querying data from a database, or using distributed computing tools like PySpark.
35. What libraries would you use for data manipulation and analysis?
For data manipulation and analysis in Python, there are a few key libraries that are widely used:
1. Pandas:
This is one of the most popular libraries for data manipulation. It provides easy-to-use data structures like DataFrames and functions to clean, transform, and analyze data. Pandas is perfect for handling structured data, like CSV files or Excel sheets.
import pandas as pd
df = pd.read_csv('data.csv')
2. NumPy:
This library is great for numerical computations and handling arrays. It’s very fast for mathematical operations and is often used alongside Pandas.
import numpy as np
array = np.array([1, 2, 3, 4])
3. SciPy:
SciPy is useful for scientific computing tasks, such as linear algebra, optimization, and signal processing. It complements NumPy with additional functionality for more complex calculations.
from scipy import stats
result = stats.norm.cdf(1.96)
4. Matplotlib and Seaborn:
These libraries are great for data visualization. Matplotlib is highly customizable, and Seaborn is built on top of it, making it easier to create beautiful and informative visualizations.
import matplotlib.pyplot as plt
plt.plot([1, 2, 3], [4, 5, 6])
plt.show()
5. Dask:
Dask is useful for working with larger-than-memory datasets and parallel computing. It can scale Pandas operations and handle larger datasets efficiently.
import dask.dataframe as dd
df = dd.read_csv('large_data.csv')
6. PySpark:
For very large datasets and distributed computing, PySpark is a powerful library that allows for big data processing using Spark.
from pyspark.sql import SparkSession
spark = SparkSession.builder.appName('app').getOrCreate()
In summary, Pandas and NumPy are your go-to for basic manipulation and analysis. If you need scientific computing, use SciPy. For visualizations, go with Matplotlib and Seaborn. For larger datasets, Dask or PySpark is ideal.
36. Describe how you would implement a logistic regression model in Python.
To implement a logistic regression model in Python, I would typically use Scikit-learn, which is a popular machine learning library. Here’s a step-by-step approach:
- Import necessary libraries: You need to import the required libraries, such as Pandas for data handling and Scikit-learn for model building.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
2. Load and preprocess the data: You can load the dataset using Pandas and split it into features (X) and the target variable (y).
# Example: Load a CSV file
data = pd.read_csv('data.csv')
# Split features and target variable
X = data[['feature1', 'feature2']] # Feature columns
y = data['target'] # Target column (binary classification)
3. Split the data into training and testing sets: It’s important to split the data so that you can evaluate the model later.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
4. Create and train the logistic regression model: You create an instance of the LogisticRegression class and train the model using the training data.
model = LogisticRegression()
model.fit(X_train, y_train)
5. Make predictions: After training the model, you use it to make predictions on the test set.
y_pred = model.predict(X_test)
6. Evaluate the model: You can measure the performance of the model using accuracy or other metrics like precision, recall, or the F1 score.
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
In summary, I would use Scikit-learn to load the data, split it into training and testing sets, train a logistic regression model, make predictions, and then evaluate the model using accuracy or other metrics.
37. What is SQL, and why is it important in data science?
SQL, or Structured Query Language, is a programming language used to manage and query relational databases. In data science, SQL is crucial because it allows you to retrieve, update, and manipulate data stored in databases. Most data used in data science projects comes from databases, so knowing SQL helps you efficiently extract and work with that data.
SQL is important because:
- Data extraction: SQL allows you to quickly access the data you need, which is a key part of preparing data for analysis.
- Data manipulation: You can filter, join, aggregate, and transform data using SQL, making it ready for analysis or modeling.
- Relational databases: Most organizations store data in relational databases, so SQL is essential for interacting with these systems.
In short, SQL is important because it’s the tool that connects data scientists to the data they need to analyze, making it an essential skill for any data science role.
38. Write a SQL query to find the average sales from a sales table
To calculate the average sales from a sales table, you can use the AVG() function in SQL. Here’s the query:
SELECT AVG(sales_amount) AS average_sales
FROM sales_table;
This query will calculate the average value of the sales_amount column from the sales_table. The result will be labeled as average_sales.
39. What is the difference between INNER JOIN and LEFT JOIN?
The main difference between INNER JOIN and LEFT JOIN lies in how they handle unmatched records between tables.
- INNER JOIN: It returns only the rows where there is a match in both tables. If there’s no match, those rows are excluded from the result.
SELECT a.column1, b.column2
FROM table_a a
INNER JOIN table_b b ON a.id = b.id;
In this example, only rows where a.id matches b.id in both tables will be included in the result.
LEFT JOIN (or LEFT OUTER JOIN): It returns all rows from the left table (table_a), and the matched rows from the right table (table_b). If there’s no match, it will still return the rows from the left table, with NULL values for the columns from the right table.
SELECT a.column1, b.column2
FROM table_a a
LEFT JOIN table_b b ON a.id = b.id;
- Here, all rows from
table_aare returned, whether or not there’s a matchingidintable_b. If no match is found, columns fromtable_bwill containNULL.
So, INNER JOIN focuses on matching rows, while LEFT JOIN ensures all rows from the left table are included, even if there’s no match.
40. How would you optimize a slow SQL query?
To optimize a slow SQL query, I would follow these steps:
- Check indexes: Make sure the relevant columns, especially those in
WHERE,JOIN, andORDER BYclauses, are properly indexed. Indexes speed up data retrieval. - **Avoid SELECT ***: Instead of selecting all columns, I would specify only the columns I need. This reduces the amount of data the query processes.
SELECT column1, column2 FROM table_name;
3. Use query execution plan: I would analyze the query execution plan to understand how the database processes the query and identify bottlenecks like full table scans.
4. Use LIMIT when appropriate: If I only need a few records, adding LIMIT reduces the workload.
SELECT column1, column2 FROM table_name LIMIT 100;
5. Optimize JOINs: Ensure that I’m joining on indexed columns and using appropriate JOIN types based on the query requirements.
6. Avoid subqueries: Replace subqueries with JOINs or common table expressions (CTEs) when possible, as they often perform better.
WITH cte AS (SELECT id FROM table1)
SELECT * FROM cte JOIN table2 ON cte.id = table2.id;
7. Filter early: Use WHERE clauses to filter data as early as possible in the query, reducing the amount of data being processed.
8. Optimize data types: Ensure that data types are appropriate. For example, using VARCHAR(255) for small text fields may be unnecessary.
By following these steps, I can significantly improve the performance of a slow SQL query.
Data Visualization
41. Why is data visualization important?
Data visualization is important because it helps make complex data more understandable and accessible. By turning raw data into visual formats like charts, graphs, or heatmaps, it becomes easier to identify trends, patterns, and insights.
Here’s why it matters:
- Simplifies data: Visuals make it easier to grasp large and complex data sets quickly.
- Identifies patterns: It helps in spotting trends and outliers that might not be obvious from raw data.
- Improves decision-making: Visualized data can provide clear, actionable insights, helping businesses make informed decisions faster.
- Engages audiences: People are more likely to pay attention to and understand data when it’s presented visually.
In short, data visualization turns data into a story that is easier to interpret, share, and act upon.
42. What tools do you prefer for data visualization?
I prefer using several tools depending on the task:
- Matplotlib and Seaborn: For Python-based projects, these are great for detailed and customizable visualizations. Matplotlib is flexible, and Seaborn adds beautiful, statistical plots with less effort.
- Tableau: For interactive and business-focused visualizations, I find Tableau very useful. It’s user-friendly and allows for creating interactive dashboards quickly.
- Power BI: Similar to Tableau, but it integrates well with Microsoft products. I like using it for presenting reports and insights in a corporate setting.
- Plotly: For web-based, interactive graphs, Plotly is a great tool. It’s especially good when I want to create dynamic visualizations.
These tools help me communicate data insights effectively, whether in exploratory analysis or final presentations.
43. Explain the concept of a confusion matrix
A confusion matrix is a tool used to evaluate the performance of a classification model. It breaks down predictions into four categories, helping you see where the model is making correct or incorrect predictions.
- True Positive (TP): The model correctly predicted a positive class.
- True Negative (TN): The model correctly predicted a negative class.
- False Positive (FP): The model predicted a positive class, but it was actually negative (also called a Type I error).
- False Negative (FN): The model predicted a negative class, but it was actually positive (also called a Type II error).
The confusion matrix gives a clear picture of how well the model is performing, showing the exact number of correct and incorrect predictions in each category. From this, you can calculate other metrics like accuracy, precision, recall, and F1 score to get a more detailed understanding of the model’s effectiveness.
44. How do you interpret a ROC curve?
A Receiver Operating Characteristic (ROC) curve is a graphical representation used to assess the performance of a classification model at various threshold levels. Here’s how to interpret it:
- Axes: The ROC curve plots the True Positive Rate (TPR) against the False Positive Rate (FPR). TPR is the proportion of actual positives correctly identified, while FPR is the proportion of actual negatives incorrectly identified as positives.
- Curve Shape: The closer the curve follows the left-hand border and the top border of the plot, the better the model is at distinguishing between the classes. A curve that goes straight to the top left corner indicates a perfect model.
- Area Under the Curve (AUC): The AUC provides a single value that summarizes the overall performance of the model. AUC values range from 0 to 1:
- 0.5: No discrimination (random guessing).
- 0.7 – 0.8: Acceptable performance.
- 0.8 – 0.9: Good performance.
- 0.9 – 1: Excellent performance.
- Threshold Selection: The ROC curve helps in selecting the optimal threshold for classification. By looking at the trade-off between TPR and FPR at different thresholds, you can choose a point that balances sensitivity and specificity according to your requirements.
In summary, the ROC curve is a valuable tool for evaluating how well a model can differentiate between classes across various thresholds, with the AUC providing an easy-to-understand performance metric.
45. What are box plots, and what do they represent?
A box plot, also known as a whisker plot, is a graphical representation of the distribution of a dataset. It provides a visual summary of key statistical measures, making it easy to understand the data’s spread and identify outliers. Here’s what it represents:
- Components:
- Box: The central box shows the interquartile range (IQR), which contains the middle 50% of the data. The lower edge represents the first quartile (Q1), and the upper edge represents the third quartile (Q3).
- Median Line: A line inside the box indicates the median (Q2) of the data.
- Whiskers: The lines extending from the box (whiskers) indicate the range of the data. Typically, they extend to 1.5 times the IQR from the quartiles.
- Outliers: Data points that fall outside the whiskers are considered outliers and are often shown as individual points.
- What it Represents:
- Central Tendency: The median gives a quick sense of the central value of the data.
- Variability: The size of the box (IQR) shows how spread out the middle half of the data is.
- Outliers: It highlights unusual data points that may require further investigation.
Overall, box plots are useful for comparing distributions across different groups, identifying outliers, and gaining insights into the data’s range and symmetry. They are particularly helpful in exploratory data analysis, allowing for quick visual assessments of the data’s characteristics.
46. How do you choose the right type of chart for your data?
Choosing the right type of chart depends on the nature of your data and the message you want to convey. Here are some key considerations:
- Type of Data:
- Categorical Data: For data divided into categories (e.g., types of fruits), bar charts or pie charts work well. Bar charts are great for comparing categories, while pie charts show proportions.
- Numerical Data: For continuous data (e.g., heights or weights), line charts or scatter plots are suitable. Line charts show trends over time, while scatter plots illustrate relationships between two numerical variables.
- Number of Variables:
- Simple charts like histograms or bar charts are effective for one variable. When analyzing two variables, scatter plots can help explore correlations, while line charts work well for time series data. To compare multiple variables, consider using grouped bar charts, stacked area charts, or multi-line charts.
- Comparison vs. Composition:
- If you want to compare values, bar charts, line charts, or dot plots are good options.
- If you want to show how parts contribute to a whole, stacked bar charts or area charts are more appropriate.
- Audience: Consider your audience’s familiarity with different types of charts. For instance, simpler charts may be better for a general audience, while more complex visualizations can be used for a data-savvy group.
- Clarity and Simplicity: Choose a chart that presents your data clearly. Avoid cluttered visuals, and make sure the chart highlights the key message without unnecessary distractions.
By considering these factors, you can select a chart type that best communicates your data’s story and helps your audience understand the insights effectively.
47. What is Tableau, and how is it used in data science?
Tableau is a powerful data visualization tool that helps people understand their data through interactive and shareable dashboards. It allows users to connect to various data sources, including spreadsheets, databases, and cloud services, making it versatile for data analysis.
Here’s how Tableau is used in data science:
- Data Visualization: Tableau enables users to create a wide range of visualizations, such as bar charts, line graphs, scatter plots, and maps. These visualizations help in identifying trends, patterns, and outliers in the data.
- Interactive Dashboards: Users can build interactive dashboards that allow stakeholders to explore the data. They can filter and drill down into the visualizations to gain deeper insights without needing to run complex queries.
- Data Integration: Tableau can connect to multiple data sources simultaneously. This feature allows data scientists to combine datasets from different platforms, enabling a comprehensive analysis.
- Real-Time Data Analysis: With Tableau, users can analyze data in real time, making it easier to respond to changes and monitor key performance indicators (KPIs) as they happen.
- Collaboration and Sharing: Tableau makes it simple to share insights with team members and stakeholders. Users can publish dashboards to Tableau Server or Tableau Online, allowing others to access and interact with the visualizations securely.
- User-Friendly Interface: Tableau has a drag-and-drop interface that makes it accessible to users without a strong technical background. This feature helps bridge the gap between data scientists and non-technical stakeholders.
In summary, Tableau is an essential tool in data science for its ability to transform complex data into understandable visuals, enabling better decision-making and communication of insights.
48. Describe a time when you had to present data to a non-technical audience
In my previous role, I was tasked with presenting the results of a customer satisfaction survey to our marketing team. The audience included team members who had strong marketing backgrounds but limited technical expertise in data analysis.
To make the presentation effective, I focused on several key strategies:
- Simplifying Data: I summarized the survey findings into a few key metrics, such as overall satisfaction scores and common feedback themes. Instead of overwhelming them with raw data, I created easy-to-understand visuals using charts and graphs to illustrate trends.
- Using Clear Visuals: I designed slides with clear, colorful visuals. For example, I used bar charts to compare satisfaction scores across different customer segments. This helped the audience quickly grasp the main points without getting lost in details.
- Telling a Story: I framed the presentation as a story, highlighting key insights and their implications for our marketing strategies. I began with an overview of the survey’s purpose, followed by the findings, and concluded with actionable recommendations based on the data.
- Encouraging Interaction: During the presentation, I encouraged questions and discussion. This not only engaged the audience but also allowed me to clarify any misunderstandings and emphasize the relevance of the data to their work.
- Relating Data to Their Experience: I used examples from our marketing campaigns that related to the survey results. For instance, I pointed out how specific marketing strategies impacted customer satisfaction, making the data more relatable and actionable for them.
Overall, the presentation was well-received. The marketing team appreciated the clear visuals and actionable insights. This experience reinforced the importance of tailoring data presentations to the audience’s level of understanding and context.
49. How do you visualize outliers in your data?
Visualizing outliers is crucial for understanding the data and identifying potential issues. Here are several methods I typically use:
- Box Plots: Box plots are one of my favorite tools for spotting outliers. They display the median, quartiles, and potential outliers in a dataset. Any data points that fall outside the whiskers are considered outliers, making it easy to spot extreme values at a glance.
- Scatter Plots: Scatter plots are great for visualizing the relationship between two variables. By plotting the data points, I can easily identify outliers that fall far away from the main cluster of points. This method works well for detecting outliers in bivariate datasets.
- Histogram: A histogram provides a visual representation of the distribution of data. By analyzing the shape of the histogram, I can identify if there are any bars with unusually high or low frequencies, indicating the presence of outliers.
- Z-Score or Modified Z-Score: After calculating the z-scores for each data point, I can visualize them using a scatter plot. Points with a z-score above a certain threshold (usually ±3) can be marked as potential outliers. This method helps quantify outliers based on how far they deviate from the mean.
- Heatmaps: When dealing with larger datasets, I often use heatmaps to visualize data density. Areas with significantly different colors may indicate the presence of outliers or unusual data patterns.
- Pair Plots: For multivariate data, pair plots allow me to visualize relationships across multiple dimensions. Outliers may appear as points that do not fit the general patterns in the plots, helping to identify unusual observations in the dataset.
By using these visualization techniques, I can effectively identify and analyze outliers, which helps in making informed decisions about data cleaning and preprocessing.
50. What is the purpose of using scatter plots?
Scatter plots serve several important purposes in data analysis:
- Relationship Visualization: They are primarily used to visualize the relationship between two continuous variables. By plotting each variable on the x-axis and y-axis, I can quickly see how they correlate with each other. For instance, if I’m analyzing the relationship between advertising spend and sales revenue, a scatter plot helps me observe whether higher spending correlates with increased sales.
- Identifying Trends: Scatter plots can reveal trends in data. If points follow a clear upward or downward pattern, it suggests a positive or negative correlation, respectively. This trend can help guide further analysis or modeling.
- Spotting Outliers: They are excellent for identifying outliers or unusual data points that do not fit the general pattern. For example, if most points cluster around a certain area and a few are far away, those outliers might warrant further investigation.
- Understanding Variability: Scatter plots allow me to see how much variability exists between the two variables. If the points are tightly clustered, it indicates a strong relationship. If they are widely spread out, the relationship may be weak.
- Multi-Dimensional Analysis: By using different colors, shapes, or sizes for data points, I can include additional dimensions in the scatter plot. For instance, I can represent a third variable (like customer segment) through color, allowing for a more comprehensive view of the data.
- Facilitating Predictions: When fitted with a regression line, scatter plots can help visualize predictions and assess how well the model fits the data. This aids in understanding the effectiveness of the model in explaining the relationship between the variables.
Overall, scatter plots are a versatile tool in data analysis, providing insights into relationships, trends, outliers, and variability. They make complex data more understandable and visually appealing, which is essential for effective communication of findings.
Conclusion
In conclusion, preparing for a data science interview can feel overwhelming, but understanding the key questions and topics can significantly boost your confidence and performance. This list of the Top 50 Data Science Interview Questions covers essential concepts, tools, and methodologies that are commonly asked in interviews at leading tech companies. By familiarizing yourself with these questions, you’ll not only enhance your knowledge but also showcase your skills and readiness to tackle real-world data challenges.
Remember, the journey doesn’t end here. Continue to explore and practice, and stay tuned for Part 2, where we’ll delve into even more questions that can help you excel in your data science career. Best of luck on your interview journey!
Part 2 Click Here
External Resources
Kaggle: Offers a wide range of tutorials, projects, and coding challenges. Kaggle’s community discussions often include interview experiences and question sets.
GeeksforGeeks: Has a dedicated section for data science interview questions, covering topics like machine learning, statistics, and coding.
Towards Data Science: A Medium publication with articles covering data science interview questions, preparation tips, and industry insights.


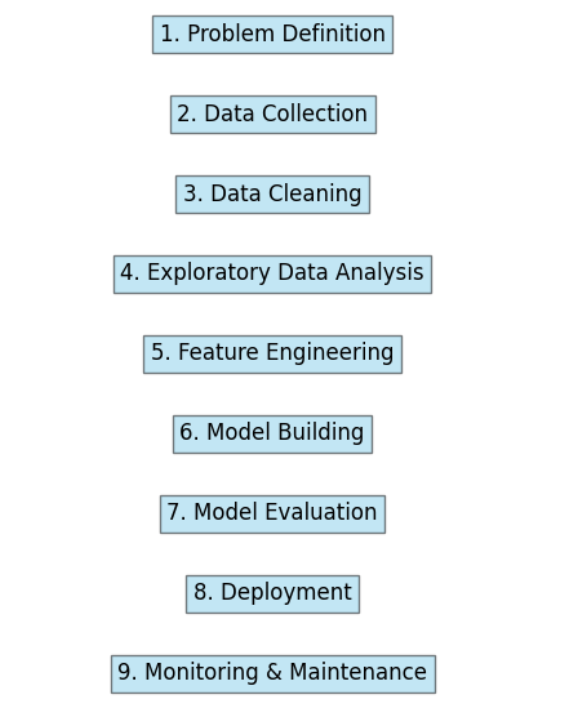





Leave a Reply