Bayes Theorem in Data Science: A Complete Guide
Introduction
Imagine you have some information, but not everything, and need to make a decision. For example, you might guess the chance of rain based on yesterday’s weather or check how accurate a medical test result is.
This is where Bayes’ Theorem helps. It lets you update probabilities when new information becomes available. Simply put, it helps you calculate the chance of one event happening, knowing that another event has already occurred.
Bayes’ Theorem is useful in data science, machine learning, medical diagnosis, and even spam filtering. In this blog, we’ll explain it with easy examples and a simple formula so you can understand it clearly.
You’ll learn why sample space matters, what posterior probability is, and how Bayes’ Theorem turns data into insights. By the end, you’ll see why this concept is so important in data science and AI. Let’s get started—you’ll be surprised at how useful Bayes’ Theorem really is!
What is Bayes Theorem?
Bayes Theorem is a fundamental concept in probability theory that provides to update our beliefs about the probability of an event based on new evidence. In simple terms, it describes how to calculate the probability of an event A given that another event B has occurred. This is expressed mathematically as:
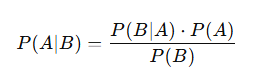
Where:
- P(A∣B) is the posterior probability: the probability of event A occurring given that B has occurred.
- P(B∣A) is the likelihood: the probability of event B occurring given that A is true.
- P(A) is the prior probability: the initial probability of event A occurring before considering the evidence B.
- P(B) is the marginal probability: the total probability of event B occurring.
Example of Bayes Theorem
Let’s consider a classic example of medical testing to illustrate Bayes’ Theorem.
Imagine you are testing for a disease that affects 1% of a population. The test is 90% accurate, meaning:
- If a person has the disease, there is a 90% chance that the test will be positive (true positive).
- If a person does not have the disease, there is a 10% chance that the test will still come back positive (false positive).
To find the probability that a person actually has the disease given that they tested positive, we apply Bayes’ Theorem:
- Define the events:
- Let D be the event that the person has the disease.
- Let T be the event that the test is positive.
- Calculate the probabilities:
- P(D)=0.01 (1% prevalence of the disease)
- P(T∣D)=0.9 (90% true positive rate)
- P(T∣¬D)=0.1 (10% false positive rate)
- Calculate P(T) (the total probability of testing positive):P(T)=P(T∣D)⋅P(D)+P(T∣¬D)⋅P(¬D)=(0.9×0.01)+(0.1×0.99)=0.009+0.099=0.108
- Apply Bayes’ Theorem:
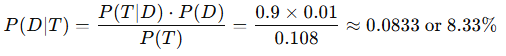
So, even with a positive test result, there is only an 8.33% chance that the person actually has the disease. This example illustrates the importance of understanding probabilities and the implications of false positives in medical testing.
Importance of Bayes Theorem in Data Science
Bayes’ Theorem is crucial in data science for several reasons:
- Informed Decision-Making: It allows data scientists to update predictions and decisions based on new data, making it an important tool for classification tasks and predictive modeling.
- Handling Uncertainty: In data science, uncertainty is a constant factor. Bayes’ Theorem provides a systematic approach to updating beliefs about hypotheses based on observed evidence.
- Applications in Machine Learning: Many machine learning algorithms, including Naive Bayes classifiers, utilize Bayes’ Theorem to predict outcomes based on input features. This is especially useful in natural language processing for tasks like spam detection and sentiment analysis.
Examples of Applications
- Spam Filtering: Bayes’ Theorem can be used to classify emails as spam or not spam based on the occurrence of specific words. For instance, if the word “free” appears frequently in spam emails, the probability of an email being spam increases if “free” is present.
- Medical Diagnosis: As illustrated earlier, it helps doctors interpret test results by providing probabilities based on prior knowledge about the disease’s prevalence.
- Risk Assessment: In finance and insurance, it aids in evaluating risks and making informed decisions based on historical data.
Historical Background and Development of Bayes Theorem
Bayes’ Theorem is named after the Reverend Thomas Bayes, an 18th-century statistician and theologian. The theorem was formulated in the 1760s when his work was published by Richard Price. Initially, it was not widely recognized but gained prominence in the 20th century with the rise of statistics and probability theory.
The theorem’s significance has grown, particularly in the context of Bayesian inference, which provides a method for updating probabilities as more evidence becomes available.

Key Developments in Bayesian Statistics:
- 19th Century: Bayes’ work was expanded upon by statisticians like Pierre-Simon Laplace, who applied it to various fields, including astronomy and biology.
- 20th Century: The advent of computers allowed for the practical application of Bayes’ Theorem in complex statistical models, revolutionizing fields like machine learning and artificial intelligence.
How Bayes Theorem Revolutionized Probability and Decision Making
Bayes’ Theorem has transformed how we approach uncertainty and decision-making across various disciplines. Its ability to integrate prior knowledge with new evidence has made it a key player in modern data science.
Key Impacts:
- Better Predictions: It improves the accuracy of predictions by allowing models to adapt as new data is introduced. This is particularly evident in machine learning, where algorithms continually refine their predictions based on incoming data.
- Complex Problem Solving: In complex and uncertain environments, such as climate modeling or financial forecasting, Bayes’ Theorem provides a framework for making informed decisions even when complete data is unavailable.
- Interdisciplinary Applications: The theorem has applications beyond statistics, influencing fields such as economics, psychology, and even philosophy, where decision-making under uncertainty is a central theme.
Key Terms and Concepts
Understanding Basic Probability Terms in Bayes Theorem
To understand Bayes Theorem, it’s helpful to know some basic probability terms. Here are a few key definitions:
- Event: An event is a specific outcome or a group of outcomes from a random process. For instance, drawing a red card from a deck is an event.
- Sample Space: This is the set of all possible outcomes of a random experiment. In our card example, the sample space includes all 52 cards in a deck.
- Random Variables: These are numerical outcomes of random events, often represented by letters like X or Y.
Conditional Probability and Bayes Theorem
Conditional probability measures how likely an event is, given that another event has already occurred. For example, if we know it’s raining, what’s the chance someone is carrying an umbrella?
Example:
- Let A be the event that it is raining.
- Let B be the event that a person is carrying an umbrella.
The conditional probability P(B∣A) tells us the chance of event BBB happening given that event A has occurred.
Understanding Prior, Likelihood, and Posterior
In Bayes Theorem, three important terms are often used:
- Prior Probability (P(A)): This is the initial probability of an event before considering new evidence. For instance, the chance that a randomly selected person is a man is our prior.
- Likelihood (P(B∣A)): This is the probability of observing the evidence if the event is true. For example, if a man claims he is a good speaker, the likelihood reflects how likely that is.
- Posterior Probability (P(A∣B)): This is the updated probability of the event after considering new evidence. After hearing the claim, we might adjust the chance that he is indeed a good speaker.
The Bayes Theorem Formula
Bayes Theorem is represented by the formula:
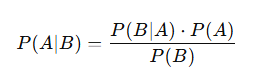
Where:
- P(A∣B) is the posterior probability.
- P(B∣A) is the likelihood.
- P(A) is the prior probability.
- P(B) is the total probability of evidence.
Applying Bayes Theorem: A Step-by-Step Example
Let’s walk through a simple example to find the probability of an event using Bayes Theorem.
Example: Imagine selecting a card from a standard deck.
- Let A be the event that the card is a heart.
- Let B be the event that the card drawn is red.
Step 1: Find P(A): The prior probability of drawing a heart is:
P(A)=13/52=1/4
(There are 13 hearts in a deck of 52 cards).
Step 2: Find P(B∣A): The likelihood of drawing a red card given that a heart is drawn is:P(B∣A)=1
(All hearts are red).
Step 3: Find P(B): The total probability of drawing a red card is:
P(B)=26/52=1/2
(There are 26 red cards: hearts and diamonds).
Step 4: Calculate P(A∣B) using Bayes Theorem:
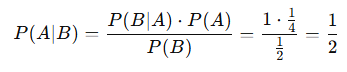
So, given that the card drawn is red, the probability that it is a heart is 50%.
Must Read
- Monotonic Sequence in Python: 7 Practical Methods With Edge Cases, Interview Tips, and Performance Analysis
- How to Check if Dictionary Values Are Sorted in Python
- Check If a Tuple Is Sorted in Python — 5 Methods Explained
- How to Check If a List Is Sorted in Python (Without Using sort()) – 5 Efficient Methods
- How Python Searches Data: Linear Search, Binary Search, and Hash Lookup Explained
Practical Applications of Bayes Theorem in Data Science
Bayes Theorem has become a cornerstone in data science, providing a framework for updating probabilities based on new information. This theorem is crucial for making informed decisions in uncertain situations. Let’s explore some real-world use cases of Bayes Theorem and understand its significance in various fields.
Real-World Use Cases of Bayes Theorem
1. Spam Filtering with Bayes Theorem
Bayes Theorem helps us update our beliefs about an event based on new evidence. It is defined by the formula:
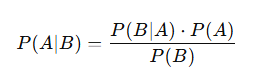
- P(A|B) is the posterior probability, the probability of event A occurring given that B is true.
- P(B|A) is the likelihood, the probability of observing B given that A is true.
- P(A) is the prior probability, the initial assessment of the probability of event A.
- P(B) is the total probability of event B occurring.
In spam filtering, event A could be an email being spam, and event B could be specific words appearing in that email.
How Does Spam Filtering Work?
When we set up a spam filter, it essentially learns from past email data. Here’s a step-by-step explanation:
- Training Data Collection:
- Past emails are collected and labeled as either spam or not spam. This labeling provides the foundation for our model.
- Calculating Conditional Probability:
- The spam filter calculates the conditional probability of specific words appearing in spam emails compared to non-spam emails. For example, words like “free,” “win,” and “offer” are commonly found in spam.
- If we find that 80 out of 100 spam emails contain the word “free,” then P(“free”∣spam)=0.8.
- Applying Bayes Theorem:
- As new emails arrive, the filter uses Bayes Theorem to calculate the probability of each incoming email being spam based on the words it contains. It continuously updates its probabilities based on the words’ occurrences.
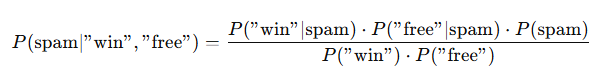
4. Decision Making:
- Based on the calculated probabilities, the spam filter makes a decision. If the probability of being spam is high enough (let’s say over 0.5), the email is classified as spam; otherwise, it is considered safe.
Applying Bayes Theorem in Python
Here’s a simple implementation in Python that demonstrates how to calculate the probability of an email being spam based on certain words.
def bayes_theorem(word, P_spam, P_not_spam, P_word_given_spam, P_word_given_not_spam):
# Calculate P(word)
P_word = (P_word_given_spam * P_spam) + (P_word_given_not_spam * P_not_spam)
# Calculate P(spam | word)
P_spam_given_word = (P_word_given_spam * P_spam) / P_word
return P_spam_given_word
# Example probabilities
P_spam = 0.4 # Prior probability of spam
P_not_spam = 0.6 # Prior probability of not spam
P_word_given_spam = 0.8 # Probability of word appearing in spam
P_word_given_not_spam = 0.1 # Probability of word appearing in non-spam
# Calculate the probability that an email is spam given the word "free"
result = bayes_theorem("free", P_spam, P_not_spam, P_word_given_spam, P_word_given_not_spam)
print(f"P(spam | 'free') = {result:.4f}")
Explanation of the Code
- The function
bayes_theoremcalculates the posterior probability that an email is spam given the presence of a specific word. - The example probabilities reflect the findings from our previous calculations.
- When you run this code, it outputs the probability that an email containing the word “free” is indeed spam.
Visualizing the Concept
To further clarify the workings of Bayes Theorem, a Venn diagram can be useful to visualize the intersections of spam and non-spam emails along with the presence of certain words.

The area where these two circles overlap represents emails that are classified as spam and also contain the word “free”.
Key Takeaways
- Bayes Theorem is fundamental in creating efficient spam filters by enabling the continuous updating of probabilities based on incoming data.
- It utilizes conditional probability to make informed decisions about the classification of new emails.
- The intersection of mathematics and programming in Python allows for practical implementations of these theories, enhancing our understanding of concepts in data science.
Application in Medical Diagnosis
In medicine, Bayes Theorem assists in evaluating the probability of a patient having a disease based on the results of diagnostic tests. Let’s break this down into simpler terms:
- Prior Probability: This refers to the prevalence of a disease in a given population. For instance, if a particular disease affects 1% of the population, this is our prior probability.
- Likelihood: This represents the accuracy of the diagnostic test, including:
- True Positive Rate: The probability that the test correctly identifies a patient with the disease.
- False Positive Rate: The probability that the test incorrectly identifies a patient as having the disease when they do not.
- Updating the Probability: When a test is performed, the results can be used to calculate the updated probability of the patient having the disease.
A Practical Example
Let’s consider a specific case to illustrate these concepts. Imagine a disease that affects 1% of the population, and a diagnostic test has a 95% accuracy rate. This means:
- Prior Probability (P(Disease)) = 0.01
- True Positive Rate (P(Positive Test|Disease)) = 0.95
- False Positive Rate (P(Positive Test|No Disease)) = 0.05
Using Bayes Theorem, we can calculate the updated probability (posterior) that a patient actually has the disease after testing positive.
Calculating P(Positive Test):
P(PositiveTest)=P(PositiveTest∣Disease)⋅P(Disease)+P(PositiveTest∣NoDisease)⋅P(NoDisease)
=(0.95×0.01)+(0.05×0.99)=0.0095+0.0495=0.059
Applying Bayes Theorem:
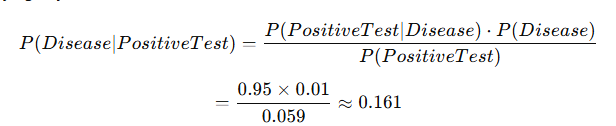
This means that even with a positive test result, the probability that the patient actually has the disease is about 16.1%. This surprising result is due to the low prevalence of the disease and the false positive rate of the test.
Importance of Prior Probability
The influence of prior probability is crucial in medical diagnosis. If the prevalence of the disease were higher, the posterior probability would increase significantly. This relationship highlights the importance of understanding both prior probabilities and test accuracy when making medical decisions.
Python Implementation
Let’s put this into a practical context by using Python to calculate the posterior probability based on various test scenarios. Here’s a simple function to do just that:
def bayes_theorem(prior, true_positive_rate, false_positive_rate):
# Calculate the probability of a positive test
p_positive = (true_positive_rate * prior) + (false_positive_rate * (1 - prior))
# Calculate posterior probability
posterior = (true_positive_rate * prior) / p_positive
return posterior
# Define parameters
prior_probability = 0.01 # 1%
true_positive_rate = 0.95 # 95%
false_positive_rate = 0.05 # 5%
# Calculate posterior probability
posterior_probability = bayes_theorem(prior_probability, true_positive_rate, false_positive_rate)
print(f"The probability of having the disease after a positive test is: {posterior_probability:.2%}")
The code defines a function, bayes_theorem, to calculate the posterior probability of having a disease after receiving a positive test result using Bayes’ Theorem.
- Parameters:
prior: The prior probability of having the disease (e.g., 1% prevalence).true_positive_rate: The probability of testing positive if the disease is present (e.g., 95%).false_positive_rate: The probability of testing positive if the disease is not present (e.g., 5%).
- Calculations:
- It calculates the total probability of a positive test (
p_positive) by combining true positive and false positive scenarios.
- It calculates the total probability of a positive test (
- Output:
- The code calls the function with defined parameters and prints the probability of having the disease after a positive test result as a percentage.
In summary, the code quantifies how prior probabilities and test accuracy affect the likelihood of having a disease after a positive result.
Application of Bayes Theorem in Finance
In finance, investors are constantly bombarded with new information—from economic reports to market trends. They must assess how this information influences the risks associated with their investments. Here’s how Bayes Theorem plays a vital role in this process:
1. Prior Knowledge: Historical Performance
Before any new information is introduced, investors rely on historical data regarding an asset’s performance. This could involve analyzing past stock trends, price movements, or the economic environment surrounding the asset.
2. New Information: Recent Market Trends
As new data becomes available—such as a positive earnings report or favorable economic indicators—investors need to incorporate this into their existing knowledge.
3. Updating Probabilities
By applying Bayes Theorem, investors can adjust their perceptions of risk and make more informed decisions. For example, let’s consider a scenario where an investor evaluates a stock:
- Prior Knowledge: The stock has shown consistent growth in the last five years (let’s denote this as event E1).
- New Information: A recent market report indicates positive economic growth (denote this as event E2).
Using Bayes Theorem, the investor updates the probability of the stock continuing to perform well based on this new information.
Example Calculation
Let’s say:
- The prior probability of the stock performing well, based on historical data, is P(E1)=0.7=0.7 (70%).
- The probability of observing positive economic growth given that the stock performs well is P(E2∣E1)=0.9 (90%).
- The total probability of observing positive economic growth in the market is P(E2)=0.8 (80%).
Using Bayes Theorem:
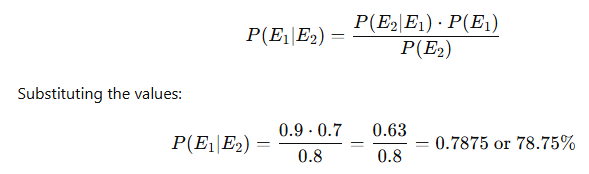
This means that, after considering the new economic report, the investor updates their belief about the stock’s potential to perform well to approximately 78.75%.
Why Is This Important?
- Informed Decision-Making: Investors who utilize Bayes Theorem can better navigate the uncertainties of the financial market. They make decisions based on updated probabilities rather than solely on gut feelings or outdated information.
- Risk Management: By continuously updating their probabilities, investors can manage risk more effectively. This dynamic approach helps in reacting to market changes swiftly.
- Enhancing Predictions: This method helps in estimating outcomes more accurately, thus enabling informed investments.
Understanding Bayes Theorem in Uncertain Situations
Bayes Theorem shines in scenarios characterized by uncertainty. It provides a systematic method for updating beliefs and making complex decisions.
- Decision Making: When faced with multiple possible outcomes, Bayes Theorem allows individuals to calculate the probabilities of various scenarios.
- Real-Time Updating: As new information becomes available, probabilities can be adjusted, leading to better-informed decisions.
Example: In weather forecasting, Bayes Theorem can be used to update the probability of rain based on new meteorological data, allowing for better planning and resource allocation.
Summary Table of Applications
| Application | Key Concepts | Keywords |
|---|---|---|
| Spam Filtering | Bayesian inference | spam filtering, filtering natural language |
| Medical Diagnosis | Predictive modeling | medical diagnosis, risk assessment, diagnosis probability |
| Finance | Risk assessment | finance, risk assessment, probability event |
| Uncertain Situations | Informed decision making | uncertain situations, complex decisions, informed decision making |
Mathematical Foundations and Proof of Bayes Theorem
Bayes Theorem is a cornerstone of probability and statistics, allowing us to update our beliefs based on new evidence. This theorem is not only foundational in mathematics but also immensely practical in fields like data science, medicine, and machine learning. Let’s explore Bayes Theorem in detail, deriving it step-by-step while providing clear examples to illustrate its applications.
Deriving Bayes Theorem Step-by-Step
Let’s break down the derivation of Bayes Theorem. This will help us understand the theorem and its applications better.
- Starting with the Definition of Conditional Probability: The conditional probability can be defined as:

4. Interpreting the Components:
- Prior Probability P(A): This is the probability of event A occurring before any evidence is taken into account.
- Likelihood P(B∣A): This reflects how probable the evidence B is if we know that A is true.
- Marginal Probability P(B): This is computed as the total probability of event B occurring, which can be calculated using the law of total probability.
Example: Medical Diagnosis
Already We have discussed this example by implementing it with Python. Now we just consider this example from a mathematical point of view
To illustrate Bayes Theorem, let’s consider a classic example in medicine:
- Let’s say we have a disease that affects 1% of the population (P(Disease)=0.01.
- A test for the disease is 90% accurate, meaning if someone has the disease, there’s a 90% chance the test will be positive (P(Positive∣Disease)=0.90.
- However, the test also has a false positive rate of 5% (P(Positive∣NoDisease)=0.05.
Now, if a patient receives a positive test result, we want to calculate the probability that they actually have the disease, P(Disease∣Positive).
Using Bayes Theorem, we can find this probability as follows:
Calculate the probabilities:
- Prior Probability: P(Disease)=0.01
- Likelihood: P(Positive∣Disease)=0.90
- Marginal Probability P(Positive):
P(Positive)=P(Positive∣Disease)⋅P(Disease)+P(Positive∣NoDisease)⋅P(NoDisease)
- Here, P(NoDisease)=1−P(Disease)=0.99:
P(Positive)=(0.90⋅0.01)+(0.05⋅0.99)=0.009+0.0495=0.0585
Apply Bayes Theorem: Now we can apply Bayes Theorem:

This means that despite a positive test result, the probability that the patient actually has the disease is about 15.4%.
Bayes Theorem in Terms of Sets and Sample Space
To further clarify Bayes Theorem, let’s discuss it in the context of sets and sample spaces.
- Sample Space: This is the set of all possible outcomes of a random experiment. For example, when drawing a card from a standard deck, the sample space includes 52 cards.
- Events: Events are subsets of the sample space. For instance, the event of drawing a heart can be represented as the set containing the 13 heart cards.
- Law of Total Probability: This law states that the total probability of an event can be found by considering all possible ways that the event can occur. It’s crucial for calculating P(B).
Using Python to Implement Bayes Theorem
Setting Up Python for Bayesian Analysis
When embarking on a journey into Bayesian analysis, setting up your Python environment is a crucial first step. This guide will help you get everything you need in place, ensuring you’re ready to explore the Bayes theorem in data science.
Why Bayesian Analysis?
Bayesian analysis offers a powerful approach to statistics. Unlike traditional methods, which often rely on fixed parameters, Bayesian techniques allow for the incorporation of prior knowledge through the use of probability distributions. This is particularly valuable when dealing with uncertainty in data.
Installing Required Libraries
To get started, you will need to install some key Python libraries. The main libraries for Bayesian analysis include:
- NumPy: Essential for numerical computations.
- SciPy: Offers modules for optimization, integration, and statistics.
- pandas: Perfect for data manipulation and analysis.
Installing Libraries
You can install these libraries using pip, the package installer for Python. Open your terminal or command prompt and run the following commands:
pip install numpy
pip install scipy
pip install pandas
Applying Bayes Theorem
Let’s consider a practical example. Suppose we have two types of cards in a deck: hearts and spades.
- Event E1E_1E1: Drawing a heart.
- Event E2E_2E2: Drawing a spade.
Assuming a standard deck of 52 cards, we can use the Bayes theorem to find the probability of drawing a heart given that a card drawn is red.
Python Code Example
Here’s how you could implement this in Python:
# Define the probabilities
P_H = 26 / 52 # Probability of drawing a red card (hearts or diamonds)
P_E1 = 13 / 52 # Probability of drawing a heart
P_E2 = 13 / 52 # Probability of drawing a spade
# Applying Bayes Theorem
P_E1_given_H = (P_E1 * P_H) / ((P_E1 * P_H) + (P_E2 * (26 / 52)))
print(f"Probability of drawing a heart given that the card is red: {P_E1_given_H:.2f}")
In this example:
- P_H is the probability of drawing a red card (hearts or diamonds).
- P_E1 and P_E2 are the probabilities of drawing hearts and spades, respectively.
- The result gives us a practical application of the Bayes theorem in assessing probabilities in a familiar context.
What Are Conditional Probabilities?
Conditional probability is the probability of an event occurring given that another event has occurred. This is often denoted as P(A∣B), which reads as “the probability of event A given event B.”
- Event A: The event whose probability we want to find.
- Event B: The event that has already occurred.
The formula for conditional probability is:
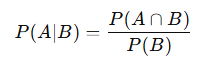
where P(A∩B) is the probability that both A and B occur.
Understanding with an Example
Let’s consider an example involving cards. Suppose we have a standard deck of 52 playing cards, and we want to find the probability of drawing a heart (event A) given that the card drawn is red (event B).
- Total Cards: 52
- Red Cards: 26 (13 hearts and 13 diamonds)
- Hearts: 13
We can calculate the conditional probability P(A∣B):
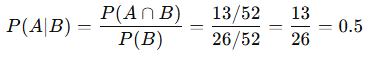
This means that if we know a card is red, there’s a 50% chance that it is a heart.
Implementing Conditional Probability in Python
Let’s see how to implement this concept using Python. We will write a function that calculates the conditional probability based on two events.
Sample Code to Calculate Conditional Probabilities
Here’s a simple Python function to calculate conditional probabilities:
def conditional_probability(event_a_and_b, event_b):
"""
Calculate the conditional probability P(A|B).
:param event_a_and_b: Probability of both A and B occurring
:param event_b: Probability of B occurring
:return: Conditional probability P(A|B)
"""
if event_b == 0:
return None # Avoid division by zero
return event_a_and_b / event_b
# Example usage
# Probability of drawing a heart (event A) and the card is red (event B)
P_A_and_B = 13 / 52 # Probability of drawing a heart
P_B = 26 / 52 # Probability of drawing a red card
P_A_given_B = conditional_probability(P_A_and_B, P_B)
print(f"The conditional probability P(Heart | Red) is: {P_A_given_B}")
Output Explanation
When you run the code, you will find:
The conditional probability P(Heart | Red) is: 0.5
This matches our earlier calculation, reinforcing the accuracy of our implementation.
Conclusion
In the rapidly evolving landscape of data science, Bayes Theorem stands out as a vital tool that offers a fresh perspective on probability and decision-making. By providing a systematic way to update our beliefs based on new evidence, Bayes Theorem enables data scientists to create models that reflect reality more accurately. Its applications range from machine learning algorithms to medical diagnoses, showcasing its versatility across various domains.
Through our exploration of Bayes Theorem in Data Science, we have uncovered its core principles and seen how it applies in practical scenarios. The use of Python for implementing Bayesian methods not only simplifies the coding process but also empowers data professionals to analyze complex datasets effectively. The step-by-step guidance provided in this blog has demonstrated how to leverage Bayesian inference to derive insights that can lead to informed decision-making.
Key Takeaways:
- Understanding Prior and Posterior Probabilities: Knowing how to define and calculate prior probabilities allows for the refinement of predictions as new data emerges.
- Practical Applications: From spam detection to predictive analytics, Bayes Theorem plays a crucial role in various data-driven applications.
- Continuous Learning: As data scientists work with real-world problems, the ability to update beliefs based on new evidence is essential for staying relevant in a data-rich environment.
- Integration with Python: Utilizing libraries such as PyMC3 and scikit-learn makes it easier to implement Bayesian models and run simulations.
Moving Forward
As you continue to explore Bayes Theorem and its applications in data science, I encourage you to experiment with your datasets using Python. Challenge yourself with new projects, whether it’s improving a model or solving a complex problem using Bayesian inference. The insights you gain will not only sharpen your analytical skills but also deepen your understanding of the intricacies of probability and decision-making.
Thank you for joining me on this exploration of Bayes Theorem in Data Science! I hope this guide serves as a helpful resource in your journey to mastering this essential concept. If you have any questions or experiences to share, feel free to comment below. Let’s keep the conversation going as we unravel the fascinating world of data together!
FAQs
What is Bayes Theorem and Why is it Important?
Bayes Theorem is a mathematical formula that describes how to update the probability of a hypothesis based on new evidence. It is important because it provides a systematic approach to reasoning about uncertainty, enabling better decision-making in various fields, including data science, medicine, and finance.
How is Bayes Theorem Used in Data Science?
In data science, Bayes Theorem is used to build probabilistic models, classify data, and make predictions. It allows data scientists to update beliefs in light of new data, making it essential for applications like spam detection, recommendation systems, and medical diagnostics.
Can Bayes Theorem Be Used for Predictive Analytics?
Yes, Bayes Theorem is a foundational tool in predictive analytics. It helps model the likelihood of future events based on prior knowledge and current data, allowing businesses to forecast trends, customer behavior, and potential risks more accurately.
What Are the Limitations of Bayes Theorem in Data Science?
The limitations of Bayes Theorem include the need for accurate prior probabilities, which can be difficult to determine. Additionally, Bayes Theorem may struggle with highly complex datasets or situations where independence assumptions do not hold. It can also be computationally intensive in some applications, particularly with large datasets.
External Resources
Coursera – Bayesian Statistics: From Concept to Data Analysis
This course offers a comprehensive introduction to Bayesian statistics and its applications in data analysis. It covers Bayesian methods and provides practical examples using Python.
Coursera Bayesian Statistics
Statistical Learning with Python: Bayesian Inference
This online resource provides a detailed overview of Bayesian inference, including theoretical concepts and practical implementation in Python. It’s a great reference for those looking to deepen their understanding.
Statistical Learning with Python







Leave a Reply