Hypothesis testing for data scientists | by Emmimal Alexander
Introduction
If you’re stepping into the world of data science, you’ve probably come across the term “hypothesis testing.” But what does it really mean? Why should you care about it? Well, let me break it down for you in simple terms.
Hypothesis testing is like a detective’s toolkit for data scientists. It helps us figure out whether our ideas about data hold up or if we need to rethink them. Whether you’re analyzing trends in customer behavior or measuring the effectiveness of a new marketing campaign, hypothesis testing can guide your decisions and provide insights based on actual data.
In this blog post, we’ll explore the ins and outs of hypothesis testing. We’ll look at what hypotheses are, how to formulate them, and the different methods we use to test them. By the end, you’ll not only understand the key concepts but also feel more confident in applying them to your projects.
So, if you want to sharpen your data science skills and make your analyses more strong, keep reading! Let’s dive into the world of hypothesis testing together.
Definition of Hypothesis Testing
So, what is hypothesis testing? Simply put, it’s a method that helps us determine if our ideas about data are correct or not. When we have a question about a dataset, we start with a hypothesis, which is just a fancy word for an educated guess. Hypothesis testing allows us to test this guess using statistical methods.
Here’s how it works:
- Formulate a Hypothesis: We start with a statement we want to test. For example, “Customers who receive a discount will buy more.”
- Collect Data: We gather relevant data that can support or contradict our hypothesis.
- Analyze the Data: Using statistical tests, we examine the data to see if it backs up our hypothesis or if we need to reject it.

Importance for Data Scientists
Now, why should you care about hypothesis testing? Well, it’s important for making informed decisions based on data. Here’s how it helps data scientists like you:
- Informed Decision-Making: Instead of making decisions based on gut feelings, hypothesis testing provides a solid foundation to back up your choices.
- Validating Assumptions: It helps confirm or challenge assumptions you might have about your data. This is crucial for improving your analysis and outcomes.
- Reducing Uncertainty: By testing your hypotheses, you can reduce uncertainty and focus on what the data is really telling you.
To put it simply, hypothesis testing is a powerful tool that can enhance your analytical skills and lead to better decision-making. Whether you’re working on a new product launch or analyzing user behavior, understanding how to test your ideas can make a world of difference.
Key Concepts in Hypothesis Testing
A. Null Hypothesis (H0)
Let’s talk about the null hypothesis, often written as H0. This is a key concept in hypothesis testing, and understanding it is super important for anyone diving into data science.
What is the Null Hypothesis?
The null hypothesis is a statement that suggests there is no effect or no difference in a given situation. It’s like saying, “Nothing is happening here.” For example, if you’re testing whether a new teaching method is better than the traditional one, your null hypothesis might be: “The new method has no effect on student performance.”
Purpose of the Null Hypothesis
So, why do we need a null hypothesis? Here are a few reasons:
- Starting Point for Testing: The null hypothesis provides a baseline. It helps you determine if your findings are significant enough to reject it.
- Framework for Analysis: By assuming that nothing is happening (the null hypothesis), you can set up your experiments and analyses to see if your data suggests otherwise.
- Statistical Testing: Most statistical tests are designed to determine whether the evidence is strong enough to reject the null hypothesis. This means you’re looking for data that contradicts H0.
Here’s how it works in a simple format:
| Aspect | Description |
|---|---|
| Definition | A statement suggesting no effect or difference. |
| Purpose | Acts as a starting point for hypothesis testing. |
| Significance | Helps in identifying whether observed data provides enough evidence to reject it. |
Why Should You Care?
The null hypothesis is a key concept in hypothesis testing, forming the foundation of your analysis. It represents the idea that there’s no significant effect or relationship in your data. Importantly, it’s the starting assumption you aim to test.
If your data doesn’t provide enough evidence to reject the null hypothesis, it suggests your findings might not be as meaningful as they seem. This makes the null hypothesis an important checkpoint for ensuring that your conclusions are reliable and not based on random chance.
Curious to know more about how the null hypothesis works and why it’s so important in data science? Let’s explore it further!
A. Null Hypothesis (H0): A Mathematical and Python Perspective
Now that we have a clear understanding of what the null hypothesis is, let’s explore it from a mathematical and Python perspective. This will give you the tools to apply hypothesis testing in your own data science projects!
Mathematical Perspective
In hypothesis testing, the null hypothesis (H0) serves as the foundation for statistical tests. When you perform these tests, you’re essentially evaluating how likely it is to observe your data if the null hypothesis is true. Here’s how it typically works mathematically:
- Define H0: Start by clearly stating your null hypothesis. For example:
- H0: The mean score of students taught with the new method is equal to the mean score of those taught with the traditional method.
- Choose a Significance Level (α): This is the threshold for deciding whether to reject H0. A common choice is 0.05, meaning you’re willing to accept a 5% chance of incorrectly rejecting the null hypothesis.
- Calculate the Test Statistic: Depending on your data and hypothesis, you might use different statistical tests (like t-tests, z-tests, etc.). The test statistic helps you determine how far your data is from what the null hypothesis suggests.
- Determine the p-value: This is the probability of observing the test results under the null hypothesis. If the p-value is less than your significance level (α), you reject H0.
Python Perspective
Now, let’s see how you can implement hypothesis testing using Python. We’ll use the popular library SciPy to perform a t-test, which is commonly used to compare the means of two groups.
Here’s a simple example:
import numpy as np
from scipy import stats
# Sample data: scores of students taught by two different methods
method_a_scores = [85, 88, 90, 92, 87]
method_b_scores = [78, 82, 80, 79, 81]
# Perform a t-test
t_statistic, p_value = stats.ttest_ind(method_a_scores, method_b_scores)
# Define significance level
alpha = 0.05
# Check if we reject the null hypothesis
if p_value < alpha:
print("Reject the null hypothesis (H0). There is a significant difference in scores.")
else:
print("Fail to reject the null hypothesis (H0). There is no significant difference in scores.")
Explanation of the Code
- Import Libraries: We import NumPy for numerical operations and SciPy for statistical testing.
- Sample Data: We create two lists representing the scores of students taught by different methods.
- t-test: We use
ttest_ind()to perform an independent t-test on the two groups. - Decision Making: Based on the p-value and significance level, we determine whether to reject or fail to reject the null hypothesis.
B. Alternative Hypothesis (Ha)
Now that we’ve covered the null hypothesis (H0), let’s talk about its counterpart: the alternative hypothesis, often symbolized as Ha. This is where things get interesting because the alternative hypothesis represents what you’re really hoping to find in your analysis.
What is the Alternative Hypothesis?
The alternative hypothesis is a statement suggesting that there is an effect or difference in the data. While the null hypothesis says, “There’s nothing special going on,” the alternative hypothesis says, “Wait, maybe something is happening here!” It’s essentially your claim that challenges the null hypothesis.
For example:
- Null Hypothesis (H0): “The new product has no impact on sales.”
- Alternative Hypothesis (Ha): “The new product does increase sales.”
In this case, the alternative hypothesis suggests that introducing the new product actually changes the sales figures, which we’re hoping to confirm through our analysis.
Why is the Alternative Hypothesis Important?
Understanding and clearly defining the alternative hypothesis is crucial because it frames the goal of your test. Here’s why it’s important for data scientists:
- Guides the Analysis: The alternative hypothesis directs the test and tells you what you’re looking for. It’s the reason you’re conducting the test in the first place.
- Helps in Decision-Making: If the data provides strong evidence against H0, you can confidently lean toward Ha. This means you’ve found something meaningful, which can impact business decisions, product development, or marketing strategies.
- Brings Objectivity: By comparing the null and alternative hypotheses, you can make objective, data-backed decisions rather than relying on assumptions.
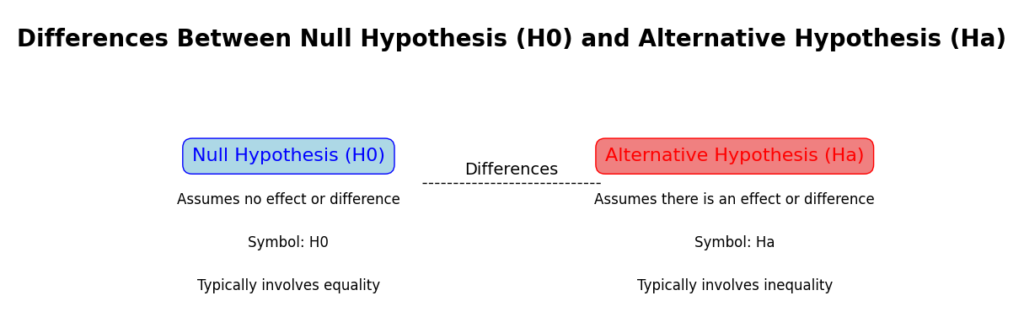
Key Differences Between H0 and Ha
To make things clear, here’s a side-by-side comparison:
| Aspect | Null Hypothesis (H0) | Alternative Hypothesis (Ha) |
|---|---|---|
| Definition | Suggests no effect or difference | Suggests there is an effect or difference |
| Purpose | Serves as a starting point | The hypothesis you hope to support |
| Decision Rule | Accepted if data doesn’t provide enough evidence | Supported if data provides strong evidence |
| Example (Sales) | “New product has no effect on sales.” | “New product increases sales.” |
Alternative Hypothesis (Ha): A Mathematical Perspective
From a mathematical viewpoint, the alternative hypothesis (Ha) is crucial because it defines what kind of evidence we’re looking for in the data. Essentially, while the null hypothesis (H0) suggests that any observed results are due to chance, the alternative hypothesis (Ha) proposes that there’s a statistically significant effect or difference.
When you conduct a hypothesis test, you’re deciding whether the data provides enough evidence to reject H0 in favor of Ha. This is typically done using a significance level (α) and a test statistic. Let’s break down the steps involved.
1. Define the Hypotheses Mathematically
Suppose you’re testing if a new drug is effective. Mathematically, your hypotheses might look like this:
- Null Hypothesis (H0): µ = µ₀, which means the drug has no effect on average (where µ₀ is the mean under H0).
- Alternative Hypothesis (Ha): µ ≠ µ₀, suggesting the drug does change the mean outcome.
In this example:
- µ represents the population mean when using the new drug.
- µ₀ represents the expected mean with no effect (as assumed by H0).
2. Set a Significance Level (α)
The significance level (α) is a threshold used to determine whether your test result is strong enough to reject H0. Common choices for α include 0.05 or 0.01. A smaller α means you require stronger evidence to reject H0.
3. Choose a Test and Calculate the Test Statistic
The type of test you choose depends on your data and what you’re testing. Here are a few common tests:
- t-test: For comparing means between two groups.
- z-test: For testing means when the sample size is large (or if population variance is known).
- Chi-square test: For testing categorical data.
Each of these tests provides a test statistic (like a t-value, z-value, etc.), which represents how far the observed data is from what we’d expect under H0. A larger test statistic means the observed data is more unusual under H0.
4. Calculate the p-value
The p-value represents the probability of observing data at least as extreme as what you have, assuming H0 is true. In other words, it measures how likely it is that the observed effect or difference happened by random chance.
- If p-value < α, you reject H0, meaning the data supports Ha.
- If p-value ≥ α, you fail to reject H0, meaning there isn’t enough evidence to support Ha.
Example of Testing Ha Mathematically
Suppose you want to test if the average height of a group of students differs from 170 cm. You could set up your hypotheses as follows:
- H0: µ = 170 cm
- Ha: µ ≠ 170 cm (two-sided test)
You’d then collect a sample of student heights, calculate the mean and standard deviation, and apply a t-test. If your test statistic is high (or low) enough and your p-value falls below α (e.g., 0.05), you’d reject H0 and conclude that there is a significant difference in height from 170 cm.
Mathematical Representation in a Table
Here’s a quick summary of how this process looks mathematically:
| Step | Description |
|---|---|
| Define Hypotheses | H0: µ = µ₀ vs. Ha: µ ≠ µ₀, µ > µ₀, or µ < µ₀ (depends on test type) |
| Set Significance Level | Typically α = 0.05 or 0.01 |
| Calculate Test Statistic | Depends on test (t, z, chi-square) |
| Determine p-value | Probability of observing the test statistic under H0 |
| Decision Rule | Reject H0 if p-value < α; fail to reject H0 if p-value ≥ α |
Testing the Alternative Hypothesis in Python
Let’s bring it into practice with a simple Python example. Suppose you’re testing whether a new training program improves employee productivity.
import numpy as np
from scipy import stats
# Sample data: hours of productivity before and after training
before_training = [6, 5, 6, 7, 5]
after_training = [7, 8, 7, 9, 8]
# Perform a paired t-test
t_statistic, p_value = stats.ttest_rel(before_training, after_training)
# Significance level
alpha = 0.05
# Check if we reject the null hypothesis in favor of the alternative hypothesis
if p_value < alpha:
print("Reject the null hypothesis (H0). The training program likely increased productivity.")
else:
print("Fail to reject the null hypothesis (H0). The training program may not have had a significant effect.")
Explanation of the Code
- Sample Data: We have two lists, one for productivity hours before and one for after training.
- Paired t-test: Since it’s the same group of employees, we use
ttest_rel()for a paired test. - Conclusion: If the p-value is less than our chosen alpha (0.05), we reject the null hypothesis, suggesting the training program probably had a positive impact.
C. Type I and Type II Errors
When you perform hypothesis testing, there’s always a risk of making mistakes. Even if you carefully define your null hypothesis (H0) and alternative hypothesis (Ha), and follow all the right steps, there’s still a chance you might reach the wrong conclusion. This is where Type I and Type II errors come in—they describe the two types of mistakes you could make during hypothesis testing.
Let’s break down each error type and why it matters.
1. Type I Error (False Positive)
A Type I error occurs when you reject the null hypothesis (H0) when it’s actually true. In other words, you think you’ve found an effect or difference, but it’s really just random chance. This is also known as a false positive.
- Example: Suppose a drug company is testing a new medication. If they reject the null hypothesis (which states the drug has no effect), they’re saying the drug works. But if this conclusion is due to random chance and not a real effect, they’ve made a Type I error.
- Probability of Type I Error: This is controlled by the significance level (α), which is often set at 0.05. So, if you’re testing at a 5% significance level, there’s a 5% chance of making a Type I error.
Why It’s Important
Type I errors can have serious consequences, especially in fields like medicine, finance, or engineering, where false positives can lead to costly or even dangerous decisions.
2. Type II Error (False Negative)
A Type II error happens when you fail to reject the null hypothesis (H0) when it’s actually false. In this case, there is an effect or difference, but the test didn’t detect it. This is known as a false negative.
- Example: Let’s go back to the drug company example. If they fail to reject H0 (concluding the drug has no effect) even though the drug actually works, they’ve made a Type II error. They’ve missed out on approving a potentially beneficial medication.
- Probability of Type II Error: This is represented by β (beta), and it depends on several factors, including sample size and effect size. The power of a test (1 – β) measures the ability of a test to correctly reject a false null hypothesis.
Why It’s Important
Type II errors can result in missed opportunities or failure to detect important findings, which can lead to overlooked solutions or unaddressed problems.
Summary Table: Type I vs. Type II Errors
Here’s a quick comparison to make things clearer:
| Error Type | Description | Example | Probability |
|---|---|---|---|
| Type I Error | Rejecting H0 when H0 is true (false positive) | Saying a drug works when it doesn’t | Significance level (α) |
| Type II Error | Failing to reject H0 when H0 is false (false negative) | Concluding a drug doesn’t work when it actually does | Beta (β) |
Minimizing These Errors
- Reduce Type I Errors: Lower your significance level (e.g., α = 0.01 instead of 0.05), but remember that this increases the chance of a Type II error.
- Reduce Type II Errors: Increase your sample size or use a more powerful test, which can help you detect smaller effects.
Understanding Type I and Type II errors can help you design better tests and make smarter decisions, so keep these concepts in mind as you work through your analysis. Both types of errors remind us that no test is perfect, and understanding these risks can help you interpret results more accurately!
Python Example to Visualize Type I and Type II Errors
For those who enjoy coding, let’s use Python to simulate what Type I and Type II errors might look like. This example will help us see the difference between a true effect and the errors we might make while testing it.
import numpy as np
from scipy import stats
# Set up parameters
true_mean = 50 # Actual mean if there's an effect
null_mean = 50 # Mean under the null hypothesis (H0)
sample_size = 30
alpha = 0.05 # Significance level
# Simulate a sample with no actual effect (H0 is true)
sample = np.random.normal(null_mean, 5, sample_size)
t_stat, p_value = stats.ttest_1samp(sample, null_mean)
# Check if we make a Type I error
if p_value < alpha:
print("Type I error: We rejected H0, but it’s actually true.")
else:
print("No Type I error: H0 was correctly not rejected.")
# Simulate a sample with a true effect (H0 is false)
sample_with_effect = np.random.normal(true_mean + 2, 5, sample_size)
t_stat, p_value = stats.ttest_1samp(sample_with_effect, null_mean)
# Check if we make a Type II error
if p_value >= alpha:
print("Type II error: We failed to reject H0, but there’s actually an effect.")
else:
print("No Type II error: We correctly detected the effect.")
This example walks through the concepts in a practical way, helping you see how these errors might arise during analysis.
D. P-Value and Significance Level (α)
Let’s talk about two key parts of hypothesis testing that come up in almost every analysis: the p-value and the significance level (α). Together, they help you decide if your results are meaningful or if they might just be random noise. Here’s what each of these terms really means and how they work together.
1. What is a P-Value?
The p-value helps you understand the likelihood of seeing your data, or something more extreme, if the null hypothesis (H0) were true. In simpler terms, it tells you how unusual or rare your results are, assuming there’s no real effect.
- Small p-value: This suggests that your data is unlikely under H0, which might mean there’s an actual effect or difference worth noting.
- Large p-value: This suggests that your data isn’t unusual under H0, making it harder to claim there’s a real effect.
A common question is, “What does ‘small’ or ‘large’ mean?” This is where the significance level (α) comes in.
2. Choosing a Significance Level (α)
The significance level, often represented as α, is the threshold you set before testing to decide how much evidence you need to reject the null hypothesis. It’s usually set at 0.05 or 5%, but can vary depending on the situation.
- α = 0.05 means you’re allowing a 5% chance of rejecting H0 when it’s actually true (Type I error).
- Lower α (like 0.01) means you want even stronger evidence to reject H0, reducing your risk of a Type I error but increasing the risk of a Type II error.
Why Significance Levels Matter
Choosing a significance level is about balancing the risk of making a mistake. A lower α makes it harder to detect effects that may actually exist (increasing Type II error), while a higher α increases the chance of finding false positives (increasing Type I error).
How P-Value and Significance Level Work Together
Once you have your p-value and your significance level, you’re ready to make a decision:
- If p-value ≤ α: You reject H0, meaning there’s enough evidence to support the alternative hypothesis (Ha).
- If p-value > α: You fail to reject H0, meaning there’s not enough evidence to support Ha.
Here’s a quick table to summarize:
| Situation | Decision | Interpretation |
|---|---|---|
| p-value ≤ α | Reject H0 | Evidence suggests there’s a real effect. |
| p-value > α | Fail to reject H0 | Not enough evidence to suggest a real effect. |
Mathematical Perspective
1. Understanding the P-Value
The p-value is the probability of obtaining test results at least as extreme as the observed data, assuming the null hypothesis (H0) is true. Mathematically, if we have a test statistic TTT, then the p-value is often expressed as:
p-value=P(T≥t∣H0)
where:
- T is the test statistic (for example, a Z-score or t-statistic),
- t is the observed value of the test statistic,
- P represents the probability under the null hypothesis.
For a two-tailed test, the p-value represents the probability of observing a value as extreme or more extreme than the one observed, on both ends of the distribution. In this case, we add the probabilities of the tail areas:
p-value=2×P(T≥∣t∣∣H0)
2. Significance Level (α)
The significance level (α) sets the threshold for how unlikely a result must be before we reject H0. It defines the critical value(s) of the test statistic. For example, in a standard normal distribution with α = 0.05 in a two-tailed test, the critical values are approximately ±1.96, meaning:
- If the test statistic lies beyond ±1.96, we reject H0.
The critical values for other distributions, like the t-distribution (often used in small samples), depend on both the significance level α and the degrees of freedom.
Python Perspective
Python has powerful libraries like SciPy that make calculating p-values straightforward. Here’s how to perform hypothesis testing using Python, with a common example: the t-test.
Example: Conducting a t-Test in Python
Suppose you want to test whether the mean of a sample is significantly different from a known population mean. Here’s how to calculate the p-value using Python.
import numpy as np
from scipy import stats
# Sample data
data = np.array([12, 14, 15, 13, 16, 14, 13, 15])
# Hypothesized population mean
mu = 14
# Perform one-sample t-test
t_statistic, p_value = stats.ttest_1samp(data, mu)
# Set significance level
alpha = 0.05
# Print results
print(f"T-statistic: {t_statistic}")
print(f"P-value: {p_value}")
# Decision
if p_value < alpha:
print("Reject the null hypothesis: There is a significant difference.")
else:
print("Fail to reject the null hypothesis: No significant difference found.")
Explanation of Code
- Data: We have a sample data set (
data) and want to check if its mean differs from a hypothesized population mean (mu). - t-test:
stats.ttest_1samp(data, mu)computes the t-statistic and p-value. - Decision Rule: We set α = 0.05, and then check if the p-value is smaller than α. If it is, we reject H0.
Interpreting Results
- T-statistic: This tells us how many standard deviations our sample mean is from the hypothesized mean.
- P-value: If this is less than α, we have evidence to reject H0.
This example illustrates how to apply hypothesis testing in Python. By combining the mathematical foundation with Python’s capabilities, you can make precise, data-driven conclusions with confidence.
Must Read
- Monotonic Sequence in Python: 7 Practical Methods With Edge Cases, Interview Tips, and Performance Analysis
- How to Check if Dictionary Values Are Sorted in Python
- Check If a Tuple Is Sorted in Python — 5 Methods Explained
- How to Check If a List Is Sorted in Python (Without Using sort()) – 5 Efficient Methods
- How Python Searches Data: Linear Search, Binary Search, and Hash Lookup Explained
The Hypothesis Testing Process
Let’s break down the process of hypothesis testing step-by-step. This will help you understand how to set up your hypotheses, pick the right test, collect data, and actually run the test. I’ll also show you where Python and math fit in to make this process even clearer.
A. Formulating Hypotheses
Before diving into any analysis, the first step is setting up your null hypothesis (H0) and alternative hypothesis (Ha). These hypotheses are like the starting point of a test, and they help frame what exactly you’re trying to find out.
- Null Hypothesis (H0): This is the statement that there’s no effect or no difference. For example, if you’re testing a new drug, H0 might be that the drug has no effect on patients’ recovery times.
- Alternative Hypothesis (Ha): This is what you want to prove. In the drug example, Ha would be that the drug does impact recovery times (either positively or negatively).
Python and Mathematical Example
Say we’re testing if the average recovery time for patients is different from a known average, like 10 days.
In Python, you’d write it out like this:
# Hypothesized mean
hypothesized_mean = 10
# Null hypothesis: mean recovery time = 10 days
# Alternative hypothesis: mean recovery time ≠ 10 days
Setting up your hypotheses clearly like this makes the analysis easier to follow and interpret.
B. Selecting the Appropriate Test
Choosing the right test is essential to make sure your results are accurate. Here are a few common tests and when you might use them:
- t-test: Used when comparing the means of two groups. For example, you’d use a t-test to see if the average recovery time for patients on a new drug is different from those on a standard drug.
- Chi-Square Test: Useful for categorical data. You might use this to test if there’s a relationship between two variables, like whether gender is associated with preference for a specific type of product.
- ANOVA (Analysis of Variance): Helps when comparing the means of three or more groups. For instance, if you’re testing the effects of three different drugs on recovery time, ANOVA would be the go-to test.
Python Example for Choosing a Test
Let’s say we want to test if the mean of a sample differs from a known value. We could use a one-sample t-test in Python:
from scipy import stats
# Sample data
data = [12, 14, 15, 13, 16, 14, 13, 15]
# Perform a one-sample t-test
t_statistic, p_value = stats.ttest_1samp(data, 10)
With these tests, Python allows you to quickly get results without manual calculations.
C. Collecting Data
The quality and size of your data sample make a big difference in hypothesis testing. Your results will only be as good as the data you’re working with. Here are some key points:
- Sample Size: Larger samples generally give more reliable results, as they better represent the population.
- Data Collection Method: Your data should be collected in a way that’s unbiased and consistent. This reduces the chance of errors or skewed results.
Mathematics Behind Sample Size
From a statistical perspective, the Central Limit Theorem tells us that larger samples tend to produce a distribution that’s closer to a normal distribution, which makes our results more accurate. Mathematically, a larger sample size (n) reduces the margin of error in your results.
Python Example for Calculating Sample Size
Python can help calculate the necessary sample size if you know the desired significance level (α) and power of the test. Here’s an example using statsmodels to find sample size for a t-test.
from statsmodels.stats.power import TTestIndPower
# Parameters for sample size calculation
effect_size = 0.5 # Small, medium, or large effect size
alpha = 0.05 # Significance level
power = 0.8 # Desired power of the test
# Calculate sample size
sample_size = TTestIndPower().solve_power(effect_size=effect_size, alpha=alpha, power=power)
print(f"Required sample size: {sample_size}")
This code will tell you how many samples you need based on the effect size you want to detect and the level of confidence you’re aiming for.
D. Conducting the Test
Now that you’ve set up your hypotheses, chosen the test, and collected data, it’s time to run the test. Conducting the test involves:
- Calculating the Test Statistic: This measures how far your data is from what you’d expect if H0 were true. For example, a t-statistic tells you how many standard deviations your sample mean is from the hypothesized mean.
- Finding the p-Value: The p-value helps you decide whether your results are statistically significant. It’s calculated based on the test statistic.
- Making a Decision: Compare the p-value to your chosen significance level (α). If the p-value is less than α, you reject H0, meaning there’s evidence to support Ha.
Python Example: Running a t-Test
Let’s put it all together with an example. Suppose we have data and want to test if its mean is significantly different from 10.
import numpy as np
from scipy import stats
# Sample data
data = np.array([12, 14, 15, 13, 16, 14, 13, 15])
# Hypothesized population mean
mu = 10
# Conduct one-sample t-test
t_statistic, p_value = stats.ttest_1samp(data, mu)
# Significance level
alpha = 0.05
# Print results
print(f"T-statistic: {t_statistic}")
print(f"P-value: {p_value}")
# Decision
if p_value < alpha:
print("Reject the null hypothesis: Significant difference found.")
else:
print("Fail to reject the null hypothesis: No significant difference found.")
Summary of Steps
Here’s a quick breakdown of each step:
| Step | Description | Python Example |
|---|---|---|
| Formulate Hypotheses | Define H0 and Ha | Define mu and data |
| Select a Test | Choose test based on data type | ttest_1samp for mean comparison |
| Collect Data | Ensure data is unbiased and of sufficient size | Use Python for sample size calculation |
| Conduct Test | Calculate test statistic and p-value | Calculate t_statistic and p_value |
| Decision | Compare p-value with α and make a conclusion | Use if statements for decision |
With each step, hypothesis testing gives you a clear way to make data-driven decisions.
Interpreting Results
Once you’ve completed a hypothesis test, the final step is to interpret the results. Understanding your findings is crucial because this is where you decide if your results are meaningful. Let’s break down the key concepts that will help you make this decision: p-values, confidence intervals, and the actual decision to accept or reject your hypothesis.
A. Understanding P-Values
The p-value is a key figure that tells us how likely it is to observe our test results if the null hypothesis (H0) is true. It essentially answers: “Are these results unusual under H0?”
Here’s how to interpret it:
- Small p-value (usually ≤ 0.05): A small p-value suggests that the observed data is unlikely under the null hypothesis. This leads us to consider rejecting the null hypothesis (meaning there might be a significant effect).
- Large p-value (> 0.05): A large p-value implies that the data is quite likely under H0. In this case, we usually fail to reject the null hypothesis (suggesting no strong evidence of a significant effect).
In simple terms, if the p-value is small, there’s something interesting going on. But if it’s large, our data doesn’t provide strong evidence of anything unusual.
Mathematical Interpretation
Mathematically, the p-value is the probability that the test statistic is as extreme as, or more extreme than, the one observed, assuming that H0 is true. So, if you have a p-value of 0.03, there’s a 3% chance that your results happened by random chance if H0 is true.
Python Example for P-Values
Let’s calculate a p-value from a t-test:
from scipy import stats
# Sample data
data = [12, 14, 15, 13, 16, 14, 13, 15]
mu = 10 # Hypothesized mean
# Perform the test
t_statistic, p_value = stats.ttest_1samp(data, mu)
print(f"P-value: {p_value}")
This code snippet will return a p-value, which you can then use to decide if the test result is statistically significant.
B. Confidence Intervals
A confidence interval (CI) gives us a range within which we expect the true value of a parameter (like the mean) to fall, with a certain level of confidence (usually 95%).
- If the confidence interval does not contain the hypothesized value (like 0 for differences), this aligns with a significant result (small p-value).
- If the confidence interval includes the hypothesized value, the result is not significant (large p-value).
Confidence intervals and p-values are related. When you have a 95% confidence interval, it corresponds to a significance level of 0.05 (α = 0.05). If a p-value is below 0.05, the hypothesized mean won’t fall within the 95% CI, suggesting a meaningful effect.
Mathematical Perspective of Confidence Intervals
The formula for a confidence interval around a sample mean is:

Python Example for Confidence Intervals
Using Python, we can calculate a confidence interval with a bit of math:
import numpy as np
import scipy.stats as stats
# Sample data
data = np.array([12, 14, 15, 13, 16, 14, 13, 15])
# Calculate mean and standard error
mean = np.mean(data)
std_err = stats.sem(data)
# Calculate confidence interval (95%)
confidence = 0.95
h = std_err * stats.t.ppf((1 + confidence) / 2, len(data) - 1)
# Confidence interval range
ci_lower = mean - h
ci_upper = mean + h
print(f"95% Confidence Interval: ({ci_lower}, {ci_upper})")
This interval gives you an estimated range where the true mean lies with 95% confidence.
C. Making Decisions
Once you’ve checked the p-value and confidence interval, it’s time to make a decision:
- Reject the Null Hypothesis: If your p-value is less than the significance level (α, typically 0.05) and the confidence interval doesn’t contain the hypothesized value, you reject H0. This suggests that your results are statistically significant, meaning there’s evidence that the effect is real.
- Fail to Reject the Null Hypothesis: If your p-value is greater than α and the confidence interval includes the hypothesized value, you fail to reject H0. This doesn’t prove H0 true but indicates there isn’t strong enough evidence to say otherwise.
Here’s a quick decision guide:
| Result | Action | Interpretation |
|---|---|---|
| Small p-value (≤ α) | Reject H0 | Significant result; evidence of an effect. |
| Large p-value (> α) | Fail to reject H0 | No significant result; not enough evidence of an effect. |
| CI excludes hypothesized value | Reject H0 | Consistent with a significant result. |
| CI includes hypothesized value | Fail to reject H0 | No significant evidence found. |
With these tools—p-values, confidence intervals, and a structured decision-making approach—you’re well-prepared to interpret hypothesis testing results confidently!
Practical Applications
Hypothesis testing might feel abstract, but it’s a powerful tool that can guide decision-making in data science and beyond. To make it more relatable, let’s look at some real-world examples of how it’s applied. We’ll also discuss common mistakes that people often make when running hypothesis tests and how to avoid these pitfalls.
A. Case Studies
Hypothesis testing is used in various fields to back decisions with data. Let’s explore a few cases where hypothesis testing has led to meaningful insights.
1. A/B Testing in Marketing
In digital marketing, A/B testing is a popular application of hypothesis testing. For example, say a company wants to test two versions of a landing page to see which one generates more sign-ups.
- Null Hypothesis (H0): Both pages perform equally well in generating sign-ups.
- Alternative Hypothesis (Ha): One page performs better than the other.
By conducting an A/B test, marketers can collect data on user interactions with each page and use a hypothesis test to determine if the observed differences in sign-ups are statistically significant.
Python Code for A/B Testing Example
Using Python, we can calculate the difference in conversion rates between two pages and run a t-test:
from scipy import stats
# Conversion data for both pages
page_a = [1 if i < 200 else 0 for i in range(1000)] # 200 conversions out of 1000 visits
page_b = [1 if i < 250 else 0 for i in range(1000)] # 250 conversions out of 1000 visits
# T-test to compare means
t_stat, p_value = stats.ttest_ind(page_a, page_b)
print(f"T-statistic: {t_stat}, P-value: {p_value}")
With a p-value less than 0.05, marketers might conclude there’s a significant difference between the two pages, helping them choose the one that maximizes conversions.
2. Medical Trials
Hypothesis testing is also key in clinical research. For instance, a researcher might want to test if a new drug is more effective than an existing one.
- Null Hypothesis (H0): The new drug has the same effectiveness as the old one.
- Alternative Hypothesis (Ha): The new drug is more effective.
By collecting data from two groups (one taking the new drug and the other taking the old one) and comparing their health outcomes, researchers can make data-backed decisions about the drug’s effectiveness.
This method ensures that the observed differences are not due to random chance, which is crucial in medical research where people’s health is involved.
3. Manufacturing Quality Control
In manufacturing, hypothesis testing can help maintain quality standards. Suppose a factory manager wants to ensure a machine produces parts within a specific tolerance level.
- Null Hypothesis (H0): The parts produced meet the quality standard.
- Alternative Hypothesis (Ha): The parts produced do not meet the quality standard.
By taking random samples of parts and measuring them, hypothesis testing can reveal if the machine is drifting from the desired tolerance, helping companies avoid costly defects.
B. Common Mistakes to Avoid
Even experienced data scientists can make errors in hypothesis testing. Here are some common pitfalls and tips on how to avoid them.
1. Misinterpreting P-Values
A common misconception is treating p-values as a direct measure of the probability of the hypothesis being true. Remember, a p-value doesn’t tell you if H0 is true or false; it simply shows the likelihood of observing your data if H0 were true.
- Solution: Use p-values to guide decisions but don’t overinterpret them. A small p-value indicates statistical significance, not certainty.
2. Ignoring Assumptions of the Test
Each statistical test has underlying assumptions. For instance, a t-test assumes normally distributed data and equal variances in both groups. Ignoring these assumptions can lead to incorrect conclusions.
- Solution: Before running a test, check that your data meets its assumptions. Python’s
scipy.statsandstatsmodelslibraries offer tools to check normality and equal variances.
from scipy.stats import shapiro, levene
# Example data for two groups
group_a = [12, 13, 14, 15, 16]
group_b = [14, 15, 16, 17, 18]
# Normality check
_, p_normality_a = shapiro(group_a)
_, p_normality_b = shapiro(group_b)
# Equal variance check
_, p_variance = levene(group_a, group_b)
print(f"P-value for normality Group A: {p_normality_a}")
print(f"P-value for normality Group B: {p_normality_b}")
print(f"P-value for equal variance: {p_variance}")
If p-values are above 0.05, the assumptions hold, and you can proceed with the test.
3. Confusing Statistical Significance with Practical Significance
Just because a result is statistically significant doesn’t mean it has real-world importance. A small effect can be statistically significant with a large enough sample size, but it might not be meaningful.
Solution: Look at the effect size, not just the p-value. Ask if the difference you found would actually make a real difference in your context.
4. Data Dredging (P-Hacking)
Data dredging, or “p-hacking,” involves running multiple tests on the same data until you find a significant result. This approach leads to false positives and unreliable findings.
Solution: Formulate hypotheses before analyzing data, and stick to them. If you must run multiple tests, adjust for multiple comparisons (e.g., with the Bonferroni correction).
5. Small Sample Sizes
Hypothesis testing relies on sufficient data to make reliable conclusions. Small samples are prone to high variance and may not provide accurate results.
Solution: Aim for an adequate sample size. Tools like Python’s statsmodels offer functions for calculating sample size based on effect size and significance level.
6. Failing to Replicate
A single test result should not be the end of the story. Replicating findings in new data is essential for building trust in your results.
Solution: Treat your initial findings as exploratory and attempt to reproduce them in a different sample or at a later time.
By understanding these practical applications and avoiding common mistakes, you can confidently apply hypothesis testing in your own data science work! Whether you’re running A/B tests, analyzing medical data, or ensuring product quality, these tools will help you turn raw data into meaningful insights.
Tools and Libraries for Hypothesis Testing
When it comes to hypothesis testing, having the right tools can make your analysis smoother and more accurate. Let’s explore some essential software and libraries that make hypothesis testing easier, especially for data scientists. We’ll also dive into some simple visualization techniques to help you understand and present your results clearly.
A. Statistical Software and Libraries
Hypothesis testing might sound intimidating, but with the right tools, you’ll be able to run tests, analyze data, and interpret results without getting lost in the math. Here are a few popular tools:
1. Python’s SciPy Library
If you’re working in Python, the SciPy library is an excellent choice for hypothesis testing. SciPy offers easy-to-use functions for many common tests, like t-tests, chi-square tests, and ANOVA. Using Python for statistical analysis is ideal if you’re already familiar with the language, and it also allows for seamless data manipulation with libraries like Pandas.
- Example Code: Let’s say you want to perform a t-test to compare the means of two groups. Here’s how you can do it with SciPy:
from scipy import stats
# Sample data for two groups
group_a = [12, 15, 14, 10, 13]
group_b = [14, 16, 15, 12, 11]
# Conduct a t-test
t_stat, p_value = stats.ttest_ind(group_a, group_b)
print(f"T-statistic: {t_stat}, P-value: {p_value}")
With this simple code, SciPy helps you decide if the difference between the two groups is statistically significant. Plus, Python’s flexibility lets you integrate these tests into larger data workflows.
2. R Programming Language
R is another powerful tool for statistical analysis. It has numerous built-in functions for hypothesis testing, and it’s widely used in academia and research due to its strong statistical capabilities.
- Quick Comparison: R is great for advanced statistical methods and visualizations. However, if you’re already familiar with Python, you might find it easier to stick with SciPy and its companion libraries (Pandas, Matplotlib, etc.) in Python.
3. Excel
For those not as comfortable with programming, Excel offers built-in tools for basic hypothesis testing, such as t-tests and chi-square tests. Excel’s data analysis add-ins make it easy to perform hypothesis tests without writing code.
- Limitations: While convenient for smaller datasets or basic tests, Excel might not be ideal for large-scale data analysis or more complex tests. But for quick, accessible testing, it’s a great starting point.
B. Visualization Techniques
Visualizing data before and after hypothesis testing can help you and your audience understand your results better. Here are a few simple, effective techniques:
1. Box Plots
Box plots are great for showing the distribution and spread of your data. They make it easy to see the median, quartiles, and potential outliers at a glance.
Example in Python: Here’s how you can create a box plot with Matplotlib to compare two groups visually:
import matplotlib.pyplot as plt
# Sample data
group_a = [12, 15, 14, 10, 13]
group_b = [14, 16, 15, 12, 11]
# Plotting box plots for both groups
plt.boxplot([group_a, group_b], labels=['Group A', 'Group B'])
plt.title('Box Plot of Group A vs. Group B')
plt.ylabel('Values')
plt.show()
- Box plots are a clear way to see how two groups differ before running a formal hypothesis test.
2. Histograms
Histograms help you visualize the distribution of your data. They’re especially useful for seeing if your data is normally distributed—a common assumption for many statistical tests.
- Example in Python:
import numpy as np
# Generate some sample data
data = np.random.normal(loc=15, scale=5, size=100)
# Plotting histogram
plt.hist(data, bins=10, color='skyblue', edgecolor='black')
plt.title('Histogram of Sample Data')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
- With a histogram, you can visually check if your data is skewed or normally distributed, helping you decide on the appropriate statistical test.
3. Scatter Plots
Scatter plots are helpful for exploring relationships between two variables. If you’re running a test to check for correlation, a scatter plot can give you an initial visual clue about any potential patterns.
- Example in Python:
# Sample data
x = [5, 10, 15, 20, 25]
y = [7, 9, 12, 15, 18]
# Plotting scatter plot
plt.scatter(x, y, color='green')
plt.title('Scatter Plot of X vs. Y')
plt.xlabel('X Values')
plt.ylabel('Y Values')
plt.show()
4. Confidence Interval Plots
When interpreting p-values, confidence intervals give additional context by showing the range within which you expect the true value to lie. Visualizing confidence intervals can make the result of hypothesis testing clearer to the audience.
- Example in Python:
import seaborn as sns
import pandas as pd
# Sample data
data = pd.DataFrame({
'Group': ['A']*10 + ['B']*10,
'Value': np.random.normal(15, 5, 10).tolist() + np.random.normal(18, 5, 10).tolist()
})
sns.pointplot(data=data, x='Group', y='Value', ci=95, capsize=0.1)
plt.title('Mean and 95% Confidence Interval')
plt.show()
This type of visualization lets you see the central tendency and the range of variation, making the hypothesis test results more meaningful.
These tools and techniques not only simplify your workflow but also make it easier to communicate your findings. With the right visualizations, even complex statistical results can be presented in an accessible way, letting your audience grasp the key takeaways at a glance.
Conclusion
In the world of data science, hypothesis testing is a powerful tool that helps you make informed decisions based on data. By understanding and applying hypothesis testing, you can validate assumptions, determine relationships between variables, and ultimately drive better insights from your analyses.
Throughout this blog post, we’ve explored the critical components of hypothesis testing, including:
- Formulating Hypotheses: Crafting clear null and alternative hypotheses lays the groundwork for your analysis.
- Understanding Errors: Recognizing the differences between Type I and Type II errors helps you assess the reliability of your conclusions.
- P-Values and Significance Levels: Knowing how to interpret p-values and set significance levels ensures that your results are statistically meaningful.
- Conducting Tests: We’ve covered the practical steps involved in executing hypothesis tests and interpreting your findings.
- Utilizing Tools and Libraries: Leveraging tools like Python’s SciPy, R, and Excel makes the process smoother and more efficient.
- Visualizing Results: Effective visualization techniques, such as box plots and histograms, allow you to communicate your results clearly to your audience.
As you continue your journey in data science, remember that hypothesis testing is not just about crunching numbers. It’s about asking the right questions and letting data guide your decisions. By applying the knowledge and techniques discussed in this post, you’ll be better equipped to tackle real-world problems and contribute valuable insights to your organization.
So, the next time you’re faced with a data-driven decision, remember the role of hypothesis testing. With practice, you’ll not only enhance your analytical skills but also become a more confident data scientist. Keep experimenting, keep learning, and let your curiosity lead the way!
External Resources
SciPy Documentation: Stats Module
- The official documentation for SciPy’s stats module offers detailed information on the statistical functions available for hypothesis testing in Python.
SciPy Stats Documentation
R Documentation: Hypothesis Testing
- For those using R, the official documentation provides resources on performing various hypothesis tests, including t-tests and ANOVA.
R Documentation on Hypothesis Testing
FAQs
What is hypothesis testing?
Hypothesis testing is a statistical method used to determine whether there is enough evidence in a sample of data to support a specific claim or hypothesis about a population. It involves formulating a null hypothesis (H0) and an alternative hypothesis (Ha), conducting a test, and making a decision based on the results.
What is the difference between a null hypothesis and an alternative hypothesis?
The null hypothesis (H0) states that there is no effect or no difference in the population, while the alternative hypothesis (Ha) suggests that there is an effect or a difference. In hypothesis testing, you aim to provide evidence to either reject H0 in favor of Ha or fail to reject H0.
What is a p-value, and why is it important?
A p-value is a measure that helps you determine the strength of the evidence against the null hypothesis. It represents the probability of observing your data, or something more extreme, if H0 is true. A smaller p-value (typically less than 0.05) indicates strong evidence against H0, leading you to consider rejecting it.
What are Type I and Type II errors?
A Type I error occurs when you incorrectly reject a true null hypothesis, concluding that there is an effect when there isn’t one (false positive). A Type II error happens when you fail to reject a false null hypothesis, concluding there is no effect when there actually is one (false negative). Understanding these errors is crucial for interpreting the results of hypothesis tests correctly.













Leave a Reply