Linear Algebra for Data Science: The Complete Guide [Part 1]

Introduction to Linear Algebra for Data Science

In data science, linear algebra plays a foundational role, underpinning key concepts and methods that shape everything from machine learning algorithms to artificial intelligence applications. It serves as the mathematical backbone that allows us to manipulate and analyze large datasets efficiently, transforming raw data into meaningful insights. Without linear algebra, processes like facial recognition, recommendation systems, or natural language processing (NLP) would be far less effective.

This first part of the guide will dive into the core principles of linear algebra and their critical importance in data science. We’ll explore vectors and matrices, key operations performed on them, and how they’re applied in machine learning models and algorithms. You’ll also see how widely-used tools like Python’s NumPy and TensorFlow use linear algebra to work with data efficiently. By understanding these essential concepts, you’ll be better equipped to tackle complex problems and optimize your models.

Linear Algebra for Data Science: The Heart of AI and Machine Learning

If you’re stepping into data science, you might hear about linear algebra everywhere. It sounds complicated, right? But in reality, it’s the foundation for so much of what we do in this field. From recommendation systems like Netflix to facial recognition on Facebook and even natural language processing (NLP), linear algebra powers the magic behind these technologies.

Let’s break down why linear algebra for data science is so important and how it’s used in real-world applications.

Why Linear Algebra Matters in Data Science

In simple terms, linear algebra is all about matrices and vectors. These are tools that help us store and manipulate data. Think of vectors as lists of numbers (kind of like rows or columns of data), and matrices as grids or tables that hold lots of these numbers.

So, why do we need them?

1. Organizing Data: When you’re working with large datasets (which is common in data science), you need a way to store and handle all that information. Matrices make it easy to organize data in a way that computers can process quickly.
2. Transforming Data: In machine learning, you’ll often have to transform data—whether it’s scaling, rotating, or compressing it. These transformations are handled using matrices. Without them, you wouldn’t be able to prepare your data for algorithms.
3. Building Algorithms: Many machine learning models, like linear regression or neural networks, use matrices to learn patterns in data. The way these algorithms “learn” is through operations like matrix multiplication, which sounds complex but is crucial for making predictions.

Real-World Uses of Linear Algebra in Data Science

Let’s look at how linear algebra for data science helps in real-world applications:

• Recommendation Systems: Ever wonder how Netflix knows what movies or shows you might like? They use your past viewing history and compare it with millions of other users, turning your preferences into vectors. These vectors are stored in matrices, and linear algebra helps the system predict what you’ll enjoy based on similar users.
• Facial Recognition: When Facebook suggests tagging a friend in a photo, it’s not magic—it’s linear algebra! The system breaks down images of faces into vectors, and by analyzing these, it can match the right face to the correct profile.
• Natural Language Processing (NLP): Linear algebra helps machines understand language. Words are represented as vectors, and by comparing these vectors, systems like Google Translate can figure out the meaning of a sentence and convert it into another language.

How Machine Learning and AI Rely on Linear Algebra

Many machine learning algorithms depend on linear algebra to process data and learn patterns. Here are a few examples:

• Linear Regression: This is one of the simplest algorithms in machine learning. It finds the relationship between input and output by solving equations using matrices. Here’s a little Python code to show how NumPy handles matrix multiplication:

import numpy as np

# Two example matrices
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])

# Matrix multiplication
result = np.dot(matrix1, matrix2)
print(result)

Output:

[[19 22]
[43 50]]

In this code, we’re multiplying two matrices, and the result is a new matrix. This type of operation is what happens behind the scenes in many algorithms.

• Principal Component Analysis (PCA): This technique is used to reduce the complexity of data. When you have too many features (or columns) in a dataset, PCA helps compress the data while still keeping the important parts. All of this is done with matrix transformations.
• Neural Networks: Neural networks, which are used for deep learning, are built on layers of matrices. The weights and biases in the network are stored as matrices. During training, the network adjusts these matrices to minimize errors, and that’s how it learns to make better predictions.

Tools That Rely on Linear Algebra

A few tools that data scientists use every day are built on top of linear algebra:

• NumPy: This is a Python library that makes it easy to work with matrices and vectors. It has functions for matrix multiplication, dot products, and much more.
• TensorFlow: If you’re into deep learning, you’ll eventually work with TensorFlow. It’s a library that builds and trains neural networks using matrices to store and adjust data as it learns.

Why Linear Algebra is Essential for Data Science

Without linear algebra, modern data science and machine learning wouldn’t exist. Here’s why:

• Efficient Data Handling: Matrix operations allow computers to handle massive amounts of data efficiently. Imagine having to process each data point individually—it would take forever! But with matrices, data can be processed in bulk, speeding up everything.
• Data Transformations: Transforming data is a key step in machine learning. For example, when compressing an image or reducing text dimensions for NLP tasks, matrices make it easy to apply transformations.

Key Concepts to Remember

Here’s a quick summary of the most important concepts:

Key Concepts of Linear Algebra for Data Science

What Are Vectors in Data Science?

In data science and machine learning, you will often encounter vectors as a fundamental concept. But what exactly are they, and why are they so important? Understanding vectors is crucial because they serve as building blocks for everything, from basic data manipulation to complex machine learning algorithms.

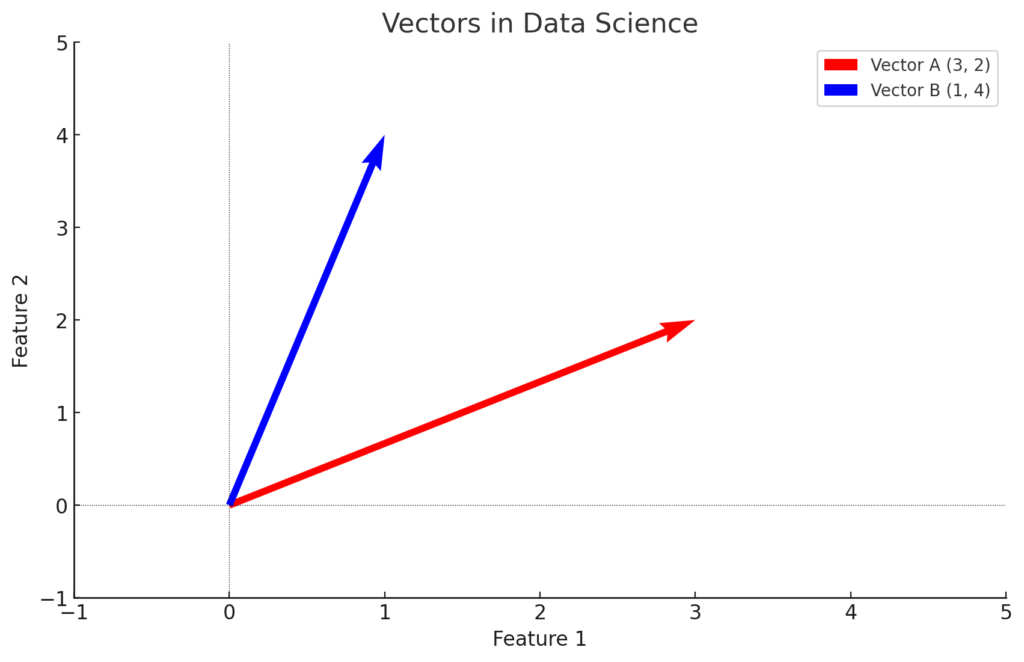
In this article, we’ll go through:

• A simple definition of vectors in data science.
• How vectors are used in machine learning.
• Key operations on vectors and why they matter.

We’ll keep it easy to understand and use real-world examples to help you grasp the concept.

Definition of Vectors

At its core, a vector is a one-dimensional array of numbers. In data science, vectors are used to represent data points. For example, if you have three features—age, height, and weight—you can represent them as a vector.

A simple vector example might look like this:

v=[28,175,70]

Here, 28 is age, 175 is height in cm, and 70 is weight in kg. Vectors can have any number of elements, depending on how many features you are working with.

How Vectors Are Used in Machine Learning

Machine learning models heavily rely on vectors. In fact, almost everything in machine learning starts with vectors. Here’s how:

1. Input Feature Vectors: When training a machine learning model, the input data (features) is usually represented as a vector. Each feature is a component of the vector. For example, in a model predicting house prices, the features might be square footage, number of bedrooms, and location, all combined into a single vector.
2. Weights and Biases: In models like linear regression or neural networks, the parameters (weights and biases) that the model learns during training are stored in vectors. These vectors are updated as the model learns to make better predictions.
3. Prediction Outputs: After processing the input through the model, the output is often a vector. For example, in multi-class classification, the model will output a vector of probabilities, each representing the likelihood of a class.

Example in Python

Here’s a quick example of an input feature vector in Python:

import numpy as np

# A vector representing age, height, and weight
input_vector = np.array([28, 175, 70])

print(input_vector)

In this code, we use NumPy to create a simple vector. The model will take this as input and use it to make predictions.

Operations on Vectors

Now, let’s move to some important operations you can perform on vectors. These operations are essential for transforming and manipulating data.

1. Vector Addition

When you add two vectors, you simply add their corresponding components. This operation is used when combining features or data points.

Example:

a=[1,2,3]

b=[4,5,6]

Adding these two vectors results in:

a+b=[1+4,2+5,3+6]=[5,7,9]

In data science, this operation might be used to combine data points or modify features.

2. Scalar Multiplication

When multiplying a vector by a scalar (a single number), each element in the vector is multiplied by that scalar. This is often used in machine learning to adjust the scale of data.

Example:

v=[1,2,3]

v×2=[1×2,2×2,3×2]=[2,4,6]

Scalar multiplication is particularly useful when scaling features in data preprocessing.

3. Dot Product

The dot product is a special operation where you multiply corresponding elements of two vectors and then sum the results. It’s crucial for many machine learning algorithms, including linear regression.

Example:

a=[1,2,3]

b=[4,5,6]

a⋅b=1×4+2×5+3×6=4+10+18=32

The dot product helps determine the similarity between two vectors and is a key operation in neural networks.

Why Vectors Matter in Data Science

So why are vectors so crucial in data science? Here’s a summary of their importance:

• Efficient Data Representation: Vectors allow you to store and represent data in an efficient way. Instead of dealing with individual data points, you can handle them all together.
• Data Manipulation: Operations like addition and scalar multiplication help transform and scale your data, making it easier to prepare for machine learning algorithms.
• Foundational in Algorithms: Many machine learning algorithms—from linear regression to deep learning—rely on vectors and their operations.

Tools for Working with Vectors in Data Science

Several tools make working with vectors easier in data science:

• NumPy: This is the go-to Python library for creating and manipulating vectors. It offers functions for vector operations like addition, scalar multiplication, and dot products.
• TensorFlow: This popular library for deep learning models heavily relies on vectors (also called tensors in this context). It provides tools to build and train neural networks that handle vector data.

Key Takeaways

• Vectors are one-dimensional arrays that represent data points or features.
• In machine learning, vectors are used in input features, weights, biases, and output predictions.
• Basic operations like vector addition, scalar multiplication, and the dot product are essential for manipulating data.

By mastering vectors, you’ll have a strong foundation for understanding more advanced linear algebra concepts in data science.

Understanding Matrices in Data Science

What is a Matrix in Data Science?

In data science, you often work with large amounts of data, and one of the best ways to organize this information is using a matrix. Understanding matrices is crucial for everything from data manipulation to building and training machine learning models.

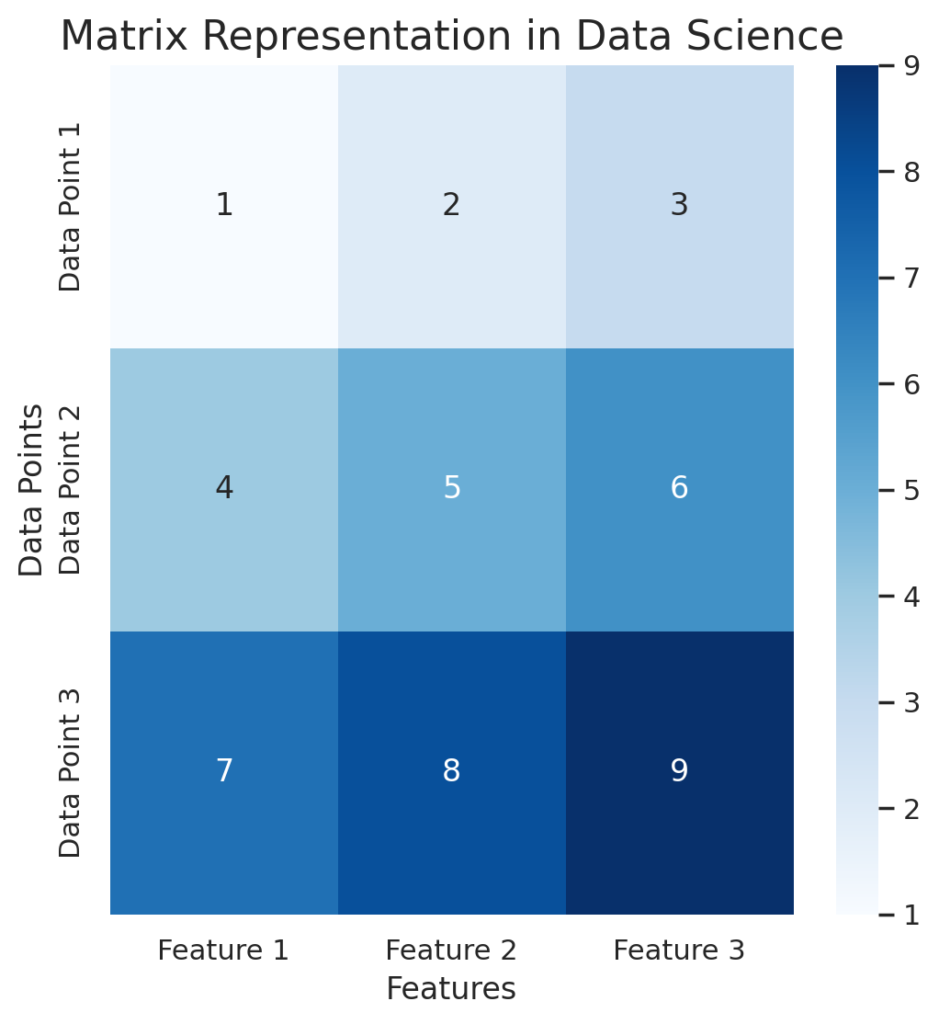
In this guide, we’ll break down:

• What a matrix is.
• How matrices represent datasets in machine learning.
• Examples of matrices in action.

We’ll keep things simple and relatable, making it easy to understand even if you’re just starting with Linear Algebra for Data Science.

Definition of a Matrix

A matrix is essentially a two-dimensional array of numbers arranged in rows and columns. In simple terms, it’s like a grid where data is organized neatly. You might already be familiar with spreadsheets or tables, and matrices follow a similar structure.

For example, this is a matrix with 3 rows and 3 columns:

In data science, the rows often represent data points (individual entries), and the columns represent features (attributes of each data point).

Matrix Representation of Data

Matrices play a crucial role in machine learning because they make it possible to organize, store, and manipulate large datasets efficiently. When working with data, you typically have multiple rows (data points) and columns (features).

For instance, if you were analyzing data for a house price prediction model, the matrix might look like this:

This table can be converted into a matrix:

Here’s what’s happening:

• Rows (horizontal) represent individual houses (data points).
• Columns (vertical) represent attributes such as size, bedrooms, and price.

By using a matrix, you can efficiently store large datasets and perform operations on them using linear algebra techniques. This is especially important when training machine learning models, where operations like matrix multiplication play a huge role.

How Matrices are Used in Machine Learning

In machine learning, matrices make it possible to handle large datasets. They allow algorithms to perform complex calculations efficiently. Here’s how matrices are commonly used:

1. Storing Datasets

As shown earlier, datasets are often represented as matrices, where each row is a data point, and each column is a feature. This makes it easy to manipulate and analyze the data using linear algebra tools.

2. Matrix Multiplication in Neural Networks

When training a neural network, matrices are used to handle input data, weights, and biases. During the forward propagation step, the input data is multiplied by the weight matrix to compute predictions.

For example, consider a simple neural network with an input matrix X and a weight matrix W:

Y=X×W

Here, the matrix multiplication allows us to process the data through the network efficiently. The output matrix Y contains the predictions.

3. Transformation of Data

In many machine learning tasks, you’ll need to perform transformations on data, such as scaling, rotating, or shifting the dataset. Matrices are used to represent these transformations and apply them to the entire dataset in a single operation.

Matrix Operations in Data Science

Working with matrices in data science involves several key operations, each of which is essential for building machine learning models. Here are some common matrix operations:

1. Matrix Addition

In matrix addition, corresponding elements of two matrices are added together. This operation is useful when combining datasets or modifying features.

Example:

If you have two matrices:

Matrix Multiplication in Data Science

Matrix multiplication plays a huge role in machine learning algorithms. It’s the foundation for many data transformations and model training processes. When we multiply two matrices, we’re combining the rows of one matrix with the columns of another to create a new matrix. This operation is central in many algorithms like linear regression, Principal Component Analysis (PCA), and neural networks.

How Matrix Multiplication Works

Matrix multiplication is not the same as element-wise multiplication (where you multiply corresponding elements of two matrices). Instead, it’s about combining rows and columns.

Here’s an example of two matrices A and B being multiplied:

Example:

Let’s say you have two matrices:

Matrix multiplication helps models process large amounts of data quickly.

Importance in Data Science

In linear regression, for example, the model calculates the best-fit line by minimizing the difference between actual and predicted values. The process involves multiplying the input data matrix by the weight matrix to generate predictions.

In neural networks, matrix multiplication happens at every layer. The input data is transformed using weight matrices, making it possible to learn patterns and make predictions.

Code Example

Let’s take a look at how matrix multiplication is implemented using Python and NumPy:

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# Matrix multiplication
C = np.dot(A, B)
print(C)

Output:

[[19 22]
 [43 50]]

This simple code multiplies two matrices, just like the earlier example.

3. Matrix Transposition in Data Science

Matrix transposition is a basic but incredibly useful operation, especially in Linear Algebra for Data Science. Transposing a matrix means flipping it over its diagonal, swapping rows with columns. This operation is commonly used in covariance matrices or when organizing data differently for calculations.

How Matrix Transposition Works

Let’s take a simple 2×2 matrix A:

For example:

By swapping the rows with the columns, we get the transpose. This operation is often necessary in algorithms that require the data in a different orientation.

Applications in Data Science

• Covariance matrices: When you calculate the covariance matrix of a dataset, matrix transposition is used to reorient the data.
• Dot products: In some calculations, such as dot products, the transpose of a matrix is required to make the multiplication valid.

4. Determinants and Inverses of Matrices

Determinants and matrix inverses are less intuitive but critical concepts in Linear Algebra for Data Science. These are used in solving systems of equations, optimizing machine learning models, and understanding matrix properties.

Determinants

The determinant of a matrix is a scalar value that can tell us things like whether a matrix is invertible (i.e., whether it has an inverse). If a matrix’s determinant is zero, it means that the matrix doesn’t have an inverse, and the data might be dependent (i.e., there is no unique solution for a system of equations).

For a 2×2 matrix:

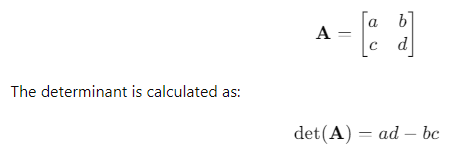
Inverses of Matrices

The inverse of a matrix is like the reciprocal of a number. When you multiply a matrix by its inverse, you get the identity matrix (which is like multiplying by 1). In machine learning, matrix inversion is used to solve systems of equations, especially in linear regression.

For example, in linear regression, to calculate the weights that minimize the error, we solve:

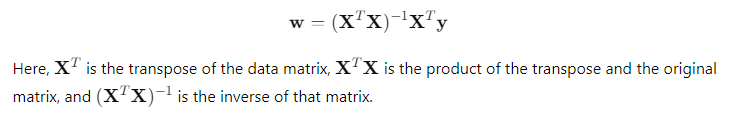
Code Example

Let’s see how we can calculate the determinant and inverse of a matrix using NumPy:

import numpy as np

A = np.array([[1, 2], [3, 4]])

# Determinant of A
det_A = np.linalg.det(A)
print("Determinant:", det_A)

# Inverse of A
inv_A = np.linalg.inv(A)
print("Inverse:\n", inv_A)

Output:

Determinant: -2.0
Inverse:
 [[-2.   1. ]
 [ 1.5 -0.5]]

Why Matrix Operations Matter in Data Science

Understanding matrix operations is not just a theoretical exercise. These operations form the backbone of most machine learning algorithms. Whether you’re using linear regression, PCA, or a neural network, matrix manipulations like multiplication, transposition, and inversion are happening under the hood.

Here’s a quick summary of why these operations matter:

• Matrix multiplication helps in transforming data and making predictions in models.
• Matrix transposition is key for organizing data and calculating covariance matrices.
• Determinants and inverses allow us to solve systems of equations, crucial for many machine learning algorithms.

Why Matrices Are Important in Data Science

• Efficient Data Handling: Matrices allow you to store and process large datasets efficiently. With matrices, you can perform mathematical operations on the entire dataset at once, which speeds up analysis and training.
• Data Transformation: In machine learning, matrices are used for scaling, normalizing, and transforming data. These transformations are essential for improving model accuracy.
• Core to Algorithms: Most machine learning algorithms rely on matrix operations. From simple linear regression to complex deep learning models, matrices power the computations behind the scenes.

Tools for Working with Matrices in Data Science

Working with matrices in data science is made easier with various tools:

• NumPy: A powerful library for matrix operations in Python. It allows you to perform matrix multiplication, addition, and other operations with ease.
• Pandas: This library is widely used for data manipulation and analysis, allowing you to store datasets in DataFrames, which are essentially matrices.
• TensorFlow: In deep learning, matrices (often called tensors) are crucial for building and training neural networks. TensorFlow helps manage these complex operations efficiently.

Key Takeaways

• Matrices are two-dimensional arrays used to represent datasets in data science.
• They play a critical role in machine learning by organizing and transforming data efficiently.
• Operations like matrix multiplication, addition, and transposition are essential for working with datasets and building algorithms.

Types of Matrices for Data Science

In the realm of data science, understanding different types of matrices is crucial. Each matrix type serves a unique purpose and can simplify various tasks, especially when dealing with data transformation, representation, and modeling. If you’re learning about Linear Algebra for Data Science, familiarizing yourself with these matrix types will greatly enhance your analytical skills.

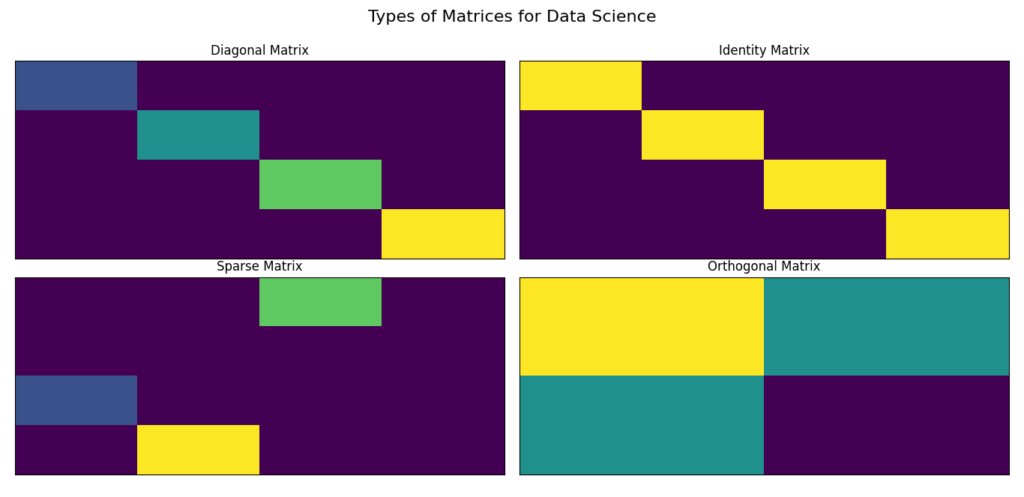
Let’s explore several key types of matrices, their significance in data science, and real-world applications.

Diagonal Matrix

In linear algebra, a diagonal matrix is a special type of matrix where all the elements outside the main diagonal are zero. This unique structure simplifies many operations in data science, making diagonal matrices valuable for various applications.

A diagonal matrix can be represented as follows:

Here, d1​, d2​, and d3​ are the non-zero elements found along the diagonal, while all other elements are zeros. This structure is not only neat but also significantly influences calculations.

Importance of Diagonal Matrices in Data Science

Diagonal matrices hold several advantages, particularly in the realm of data science:

• Simplification of Operations: When performing matrix operations, diagonal matrices can make calculations faster and simpler. For example, when multiplying a diagonal matrix with another matrix, only the diagonal elements contribute to the result, drastically reducing computation time.
• Scaling: Diagonal matrices are often used to represent scaling operations. If a diagonal matrix is multiplied by a data matrix, each feature can be scaled by different factors. This is particularly useful in preparing data for analysis.
• Representation of Variance: In techniques like Principal Component Analysis (PCA), diagonal matrices can effectively represent the variances of different dimensions. This helps in understanding how much variance each feature contributes to the overall data.

Example in Data Science

Let’s consider a practical example: a recommender system. In such systems, a diagonal matrix could represent the weights of features for different users. This approach allows each user’s preferences to be easily scaled based on their ratings, enhancing the overall accuracy of recommendations.

Python Code Example

To illustrate how to create a diagonal matrix in Python, we can use the NumPy library. Here’s a simple code snippet:

import numpy as np

# Example of a diagonal matrix
D = np.diag([1, 2, 3])
print(D)

Output:

[[1 0 0]
 [0 2 0]
 [0 0 3]]

In this example, the matrix DDD consists of three diagonal elements: 1, 2, and 3. The zeros surrounding these values confirm the defining characteristic of a diagonal matrix.

Key Characteristics of Diagonal Matrices

• Square Shape: Diagonal matrices are always square, meaning they have the same number of rows and columns.
• Efficient Computation: Many mathematical operations, such as addition or multiplication, can be performed quickly due to the presence of zeros in non-diagonal positions.
• Eigenvalues: The diagonal elements represent the eigenvalues of the matrix, providing insight into the matrix’s properties.

Benefits of Using Diagonal Matrices

The use of diagonal matrices can enhance various aspects of data analysis, including:

• Performance: Operations involving diagonal matrices tend to run faster because only the diagonal elements are active during calculations.
• Clarity: Representing data in a diagonal format can simplify visualizations and interpretations, making patterns easier to identify.
• Customization: Different scaling factors can be applied to each feature, allowing for a tailored approach to data analysis.

Incorporating diagonal matrices into your understanding of linear algebra for data science can lead to more efficient data processing and analysis. Their unique properties make them essential tools in various algorithms and methods. As you continue to explore linear algebra, remember that diagonal matrices not only simplify calculations but also offer a deeper understanding of data relationships.

Key Takeaways:

• Diagonal matrices are special matrices where only diagonal elements are non-zero.
• They simplify computations and are crucial in scaling and PCA.
• Their structure provides benefits in performance, clarity, and customization in data analysis.

Identity Matrix

An identity matrix is a special type of square matrix in linear algebra. It has a unique property: all the diagonal elements are equal to 1, while all off-diagonal elements are 0. This structure is fundamental in various mathematical computations, making it essential for anyone studying linear algebra for data science.

An identity matrix can be represented as follows for a 3×3 matrix:

Importance of the Identity Matrix

The identity matrix plays a crucial role in many areas of data science. Its importance can be broken down into several key points:

• Multiplicative Identity: Just like the number 1 is the multiplicative identity for real numbers (e.g., 1×a=a), the identity matrix serves as the multiplicative identity for matrices. When any matrix A is multiplied by the identity matrix III, the original matrix A remains unchanged:

A×I=A

• Inversion: The identity matrix is closely related to matrix inversion. When a matrix A is multiplied by its inverse A^-1, the result is the identity matrix:

A×A^−1=I

• Solving Systems of Equations: In linear regression and other machine learning algorithms, identity matrices are used to solve systems of equations. The identity matrix simplifies computations, making it easier to work with various algorithms.

Practical Example of the Identity Matrix in Data Science

Let’s say you are working with a dataset where you need to apply transformations while maintaining the original data structure. In this scenario, the identity matrix can be used to achieve that. For instance, when applying a linear transformation to a dataset, multiplying by the identity matrix ensures that some dimensions are unaffected.

Python Code Example

To demonstrate the identity matrix in Python, we can use the NumPy library. Here’s a simple code snippet that creates an identity matrix:

I = np.eye(3)
print(I)

Output:

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

In this example, the np.eye(3) function generates a 3×3 identity matrix. The output confirms that the diagonal elements are 1, while the rest are 0.

Applications of the Identity Matrix

The identity matrix finds its application in various domains, particularly in data science. Here are some key applications:

• Linear Transformations: In computer graphics and data transformations, identity matrices are used to ensure that certain transformations do not alter specific features.
• Machine Learning Algorithms: In algorithms such as linear regression, identity matrices facilitate the calculation of coefficients without affecting the input data.
• Eigenvalue Problems: Identity matrices play a significant role in finding eigenvalues and eigenvectors, which are crucial for techniques like PCA (Principal Component Analysis).

Benefits of Understanding the Identity Matrix

Gaining a solid understanding of the identity matrix provides numerous benefits:

• Enhanced Calculation Skills: Familiarity with the identity matrix can lead to quicker and more efficient calculations in matrix algebra.
• Better Algorithm Implementation: Understanding the role of the identity matrix in algorithms can improve the implementation of machine learning models.
• Clearer Data Insights: Recognizing how the identity matrix operates can lead to clearer insights when analyzing data transformations.

The identity matrix is a fundamental concept in linear algebra for data science. Its unique properties and applications make it an essential tool for various mathematical operations. By understanding the identity matrix, data scientists can improve their analytical skills and apply these concepts effectively in their work.

Key Takeaways:

• The identity matrix has diagonal elements equal to 1 and off-diagonal elements equal to 0.
• It acts as the multiplicative identity in matrix algebra.
• Understanding the identity matrix enhances skills in solving systems of equations and implementing machine learning algorithms.

Sparse Matrix

What is a Sparse Matrix?

A sparse matrix is a type of matrix in which most of the elements are zero. In data science, sparse matrices are particularly useful for representing data where only a small number of values are significant. This can occur in various scenarios, such as natural language processing, recommender systems, and image processing.

For example, consider a matrix representing user preferences for different products. If most users have not rated many products, the matrix will contain many zeros. This characteristic makes sparse matrices an essential concept in linear algebra for data science.

Characteristics of Sparse Matrices

Sparse matrices have distinct characteristics that differentiate them from dense matrices. Here are some key points:

• Storage Efficiency: Sparse matrices can be stored more efficiently than dense matrices. Instead of storing all elements, only the non-zero elements and their positions are stored. This leads to significant memory savings.
• Computational Efficiency: Operations on sparse matrices are often faster. Specialized algorithms can take advantage of the sparsity, reducing the amount of computation needed.
• Applications in Data Science: Sparse matrices are widely used in various data science applications, including:
  • Text data representation (e.g., bag-of-words models)
  • User-item interactions in recommendation systems
  • Image representation, where only a few pixels are significant

Example of a Sparse Matrix

Let’s consider a simple example of a sparse matrix:

In this 3×3 matrix, only two elements (3 and 5) are non-zero, while the rest are zeros. This matrix can be represented more efficiently by storing only the non-zero elements along with their positions.

Why Use Sparse Matrices?

Using sparse matrices in data science can provide several benefits:

• Reduced Memory Usage: By only storing non-zero elements, the amount of memory required can be significantly reduced, especially for large datasets.
• Faster Computation: Algorithms designed for sparse matrices can perform operations more quickly by ignoring the zero elements.
• Facilitation of Large-Scale Problems: Sparse matrices make it possible to handle large-scale problems, such as those encountered in machine learning and data mining.

Working with Sparse Matrices in Python

Python provides libraries such as SciPy, which include efficient ways to work with sparse matrices. Here’s a simple example demonstrating how to create and manipulate a sparse matrix using the SciPy library:

import numpy as np
from scipy.sparse import csr_matrix

# Creating a dense matrix
dense_matrix = np.array([[0, 0, 3], 
                          [0, 0, 0], 
                          [5, 0, 0]])

# Creating a sparse matrix using Compressed Sparse Row format
sparse_matrix = csr_matrix(dense_matrix)

# Displaying the sparse matrix
print(sparse_matrix)

Output:

  (0, 2)	3
  (2, 0)	5

In this code snippet, the csr_matrix function from the SciPy library is used to create a sparse matrix in Compressed Sparse Row format. The output displays the non-zero elements along with their positions, illustrating the efficiency of storage.

Applications of Sparse Matrices in Data Science

Sparse matrices are employed in various data science applications. Here are some practical examples:

• Natural Language Processing: In text analysis, sparse matrices can represent term-document matrices, where each entry indicates the presence or absence of a term in a document.
• Recommendation Systems: Sparse matrices can represent user-item interaction matrices, allowing systems to provide personalized recommendations based on limited user feedback.
• Image Processing: In image compression, sparse matrices can represent images where most pixels are zero (black) and only a few pixels have values (colored).

Importance in Data Science

Sparse matrices play a critical role in data science, especially in areas like:

• Efficiency: They save memory and computation time. By only storing non-zero elements and their positions, you can work with large datasets without unnecessary overhead.
• Recommender Systems: In collaborative filtering, user-item interaction matrices are often sparse. For instance, if a user has rated only a few items, most entries in the user-item matrix will be zero.

Example in Recommender Systems

Imagine a user-item rating matrix for a movie recommendation system. Most users won’t rate all movies, leading to a sparse matrix. Instead of storing all ratings, only the non-zero ratings will be saved.

from scipy.sparse import csr_matrix

# Create a sparse matrix (3x3)
sparse_matrix = csr_matrix([[1, 0, 0], [0, 0, 3], [4, 0, 0]])
print(sparse_matrix)

Output:

  (0, 0)	1
  (1, 2)	3
  (2, 0)	4

Orthogonal Matrices and Their Role in Data Transformation

In the world of linear algebra for data science, one of the most important concepts is that of orthogonal matrices. These matrices have special properties that make them essential in various data transformation tasks. Understanding orthogonal matrices can greatly enhance your skills in data science, especially when dealing with complex data transformations and algorithms.

What is an Orthogonal Matrix?

An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors. In simpler terms, this means that:

1. Dot Product: The dot product of any two different rows (or columns) is zero.
2. Length: Each row (or column) has a length of one.

Mathematically, a matrix A is orthogonal if it satisfies the following condition:

Visualizing Orthogonal Matrices

To visualize what orthogonality means, consider a simple example with a 2D space. Imagine two vectors v1 and v2​:

• v1=[1,0]
• v2=[0,1]

These vectors are orthogonal because they are perpendicular to each other. When represented as a matrix:

A=[[1 0​]

[0 1​]]

This is the identity matrix, which is also an orthogonal matrix. The beauty of orthogonal matrices lies in their ability to rotate and reflect data without distorting it.

Importance of Orthogonal Matrices in Data Science

Orthogonal matrices play a crucial role in data science for several reasons:

• Data Transformation: They can be used to transform data while preserving its structure. This is especially important in techniques such as Principal Component Analysis (PCA), where data is projected onto orthogonal axes.
• Numerical Stability: Operations involving orthogonal matrices are often more numerically stable than those involving arbitrary matrices. This stability is vital when performing computations in high-dimensional spaces.
• Reducing Overfitting: In machine learning, orthogonal transformations can help in feature selection and dimensionality reduction, which can lead to better models by reducing overfitting.

Example of an Orthogonal Matrix

Consider the following orthogonal matrix:

Applications of Orthogonal Matrices in Data Science

Orthogonal matrices are applied in various areas of data science, including:

• Principal Component Analysis (PCA): PCA uses orthogonal transformations to reduce dimensionality while retaining most of the variance in the dataset. This is crucial for visualizing and interpreting high-dimensional data.
• QR Decomposition: This technique is used to solve linear systems and least squares problems. QR decomposition involves decomposing a matrix into an orthogonal matrix and an upper triangular matrix, making calculations simpler and more efficient.
• Machine Learning Algorithms: Many algorithms, such as Support Vector Machines (SVM) and Neural Networks, use orthogonal transformations to optimize performance and reduce overfitting.

Code Example: Orthogonal Matrix in Python

Here’s a simple example using Python to create an orthogonal matrix and verify its properties:

import numpy as np

# Define an orthogonal matrix
Q = np.array([[1/np.sqrt(2), 1/np.sqrt(2)],
              [-1/np.sqrt(2), 1/np.sqrt(2)]])

# Calculate the transpose
Q_transpose = Q.T

# Verify orthogonality
orthogonality_check = np.allclose(Q_transpose @ Q, np.eye(2))
print("Is Q an orthogonal matrix?", orthogonality_check)

Output:

Is Q an orthogonal matrix? True

In this code snippet, the orthogonality of matrix Q is confirmed by checking if the product of Q^T and Q results in the identity matrix.

Orthogonal matrices are a vital concept in linear algebra for data science. Their unique properties enable efficient data transformations, enhance numerical stability, and play a significant role in various applications. By understanding and leveraging orthogonal matrices, data scientists can improve their analysis and modeling techniques.

Key Takeaways

• Orthogonal matrices preserve angles and distances, making them useful for data transformations.
• They offer numerical stability and can help reduce overfitting in machine learning models.
• Applications include PCA, QR decomposition, and various machine learning algorithms.

Example in Dimensionality Reduction

In PCA, the data is transformed into a new coordinate system. The axes (principal components) are chosen to be orthogonal, ensuring that each component captures as much variance as possible.

# Create an orthogonal matrix using NumPy
Q, R = np.linalg.qr(np.random.rand(3, 3))  # QR decomposition
print("Orthogonal Matrix Q:\n", Q)

Output (example):

Orthogonal Matrix Q:
 [[-0.5052786  -0.73974347 -0.44250455]
 [-0.68386848  0.05971564  0.7281658 ]
 [-0.52447045  0.67079318 -0.52696886]]

Summary of Matrix Types in Data Science

Understanding these types of matrices is essential for effective data manipulation and analysis. Here’s a quick summary:

Eigenvectors and Eigenvalues: Power of Linear Transformations

What are Eigenvectors and Eigenvalues in Data Science?

In the world of data science, understanding eigenvectors and eigenvalues is crucial for uncovering patterns and simplifying complex data. While these concepts may seem intimidating at first, breaking them down into simple terms makes them easier to grasp. This article will help you understand what eigenvectors and eigenvalues are, how they work, and their importance in data analysis. If you are diving into Linear Algebra for Data Science, this topic is essential!

Understanding Eigenvectors and Eigenvalues

Eigenvectors and eigenvalues are mathematical concepts that come from linear algebra. They are used extensively in data science, particularly in areas such as Principal Component Analysis (PCA), which is a technique for dimensionality reduction.

What are Eigenvectors?

An eigenvector is a special vector that remains in the same direction after a transformation represented by a matrix. This means that when a matrix acts on an eigenvector, the output is a scalar multiple of that eigenvector.

Mathematically, this can be represented as:

Av=λv

Here:

• A is a square matrix.
• v is the eigenvector.
• λ is the eigenvalue associated with that eigenvector.

What are Eigenvalues?

An eigenvalue is the scalar that represents how much the eigenvector is stretched or shrunk during the transformation. Essentially, it tells us whether the transformation expands or contracts the eigenvector.

In simpler terms, if you visualize the transformation of data in a 2D space, the eigenvectors point in the directions of maximum variance, while the eigenvalues tell you how much variance exists in those directions.

The Role of Eigenvectors and Eigenvalues in Finding Patterns

Eigenvectors and eigenvalues play a significant role in identifying patterns within data. They are particularly useful in various applications:

• Dimensionality Reduction: In techniques like PCA, eigenvectors help identify the most important features in a dataset. By focusing on the directions of maximum variance, data scientists can reduce the number of dimensions while retaining essential information.
• Image Compression: In image processing, eigenvectors are used to represent images in a lower-dimensional space. This helps in compressing images without losing significant quality.
• Clustering: Eigenvectors can also be used to enhance clustering algorithms, allowing data scientists to identify groupings or clusters more effectively.

Visualizing Eigenvectors and Eigenvalues

To better understand these concepts, let’s consider an example. Imagine a dataset represented in a 2D space. After applying a transformation (a matrix), the data points might change position.

• The eigenvectors will indicate the directions along which the data points are aligned.
• The corresponding eigenvalues will show how much the data points stretch or compress along those directions.

Here’s a simple visualization:

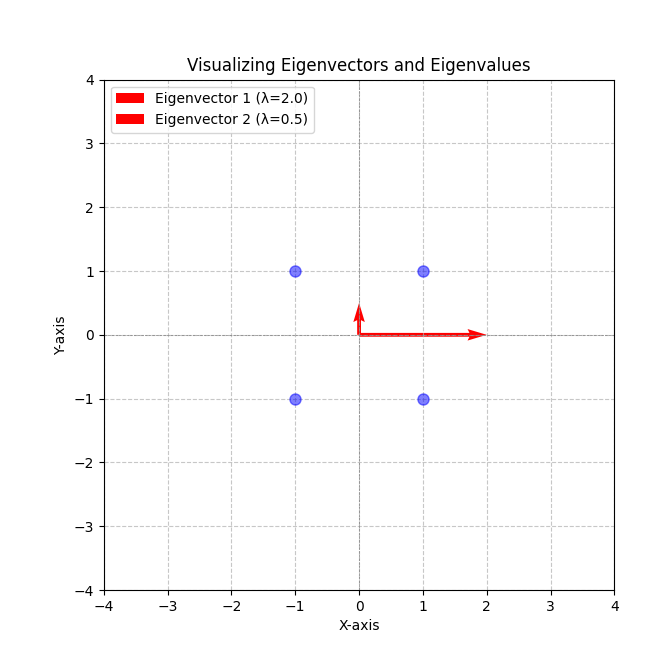
Here’s a visualization of eigenvectors and eigenvalues in a 2D space.

• The blue points represent original data points before transformation.
• The red arrows indicate the directions of the eigenvectors, with their lengths corresponding to the eigenvalues. The length of each arrow shows how much the data points stretch (for eigenvalue > 1) or compress (for eigenvalue < 1) along those directions.

This diagram helps illustrate how eigenvectors and eigenvalues relate to the transformation of data in a 2D space!

Example in Python

Let’s look at a practical example to solidify our understanding. Consider a small dataset represented as a matrix. We can compute the eigenvectors and eigenvalues using Python’s NumPy library.

import numpy as np

# Example matrix
A = np.array([[2, 1],
              [1, 2]])

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)

print("Eigenvalues:", eigenvalues)
print("Eigenvectors:\n", eigenvectors)

When you run this code, you might see output like this:

Eigenvalues: [3. 1.]
Eigenvectors:
 [[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

In this output:

• The eigenvalues 333 and 111 indicate the amount of variance along their respective directions.
• The eigenvectors point to the directions of maximum variance in the dataset.

Summary of Eigenvectors and Eigenvalues

Here’s a quick overview to reinforce our understanding of eigenvectors and eigenvalues:

Applications in Machine Learning: Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors play a crucial role in several machine learning algorithms, particularly when dealing with large datasets. By understanding their significance, you can use their power to optimize your models and make them more efficient. This article will explore their applications in Principal Component Analysis (PCA), Spectral Clustering, and how they aid in dimensionality reduction.

When you study Linear Algebra for Data Science, eigenvalues and eigenvectors become more than just mathematical tools—they help you gain deeper insights into your data and enhance your computational efficiency.

Principal Component Analysis (PCA)

Principal Component Analysis (PCA) is one of the most common techniques where eigenvectors and eigenvalues are applied. PCA is widely used for dimensionality reduction, where the goal is to reduce the number of features while preserving as much information as possible.

How PCA Uses Eigenvectors and Eigenvalues

PCA works by identifying the directions (or principal components) along which the data varies the most. These directions are represented by eigenvectors, while the magnitude of variance in each direction is given by the corresponding eigenvalues.

1. Eigenvectors help identify the directions (principal components) that capture the most variance in the dataset.
2. Eigenvalues indicate how much variance is captured in each of these directions.

Example of PCA

Let’s consider a dataset with hundreds of features (columns). By applying PCA, we can reduce this number to a smaller set of principal components, which represent the majority of the variance in the data.

For instance, if your dataset has 100 features, after applying PCA, you might reduce it to just 10 or 15 components. This reduction improves the computational efficiency of machine learning algorithms, as the model will now work with fewer features while still retaining most of the important information.

Here’s an example using Python:

import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

# Load example dataset
data = load_iris()
X = data.data

# Applying PCA
pca = PCA(n_components=2)  # Reduce to 2 dimensions
X_reduced = pca.fit_transform(X)

print("Reduced dataset shape:", X_reduced.shape)

In this case, the dataset originally had 4 features. PCA reduced it to 2 components while preserving most of the variance. These components are the eigenvectors, and their corresponding eigenvalues tell us how much variance each component captures.

Applications in Machine Learning: Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors play a crucial role in several machine learning algorithms, particularly when dealing with large datasets. By understanding their significance, you can leverage their power to optimize your models and make them more efficient. This article will explore their applications in Principal Component Analysis (PCA), Spectral Clustering, and how they aid in dimensionality reduction.

When you study Linear Algebra for Data Science, eigenvalues and eigenvectors become more than just mathematical tools—they help you gain deeper insights into your data and enhance your computational efficiency.

Principal Component Analysis (PCA)

Principal Component Analysis (PCA) is one of the most common techniques where eigenvectors and eigenvalues are applied. PCA is widely used for dimensionality reduction, where the goal is to reduce the number of features while preserving as much information as possible.

How PCA Uses Eigenvectors and Eigenvalues

PCA works by identifying the directions (or principal components) along which the data varies the most. These directions are represented by eigenvectors, while the magnitude of variance in each direction is given by the corresponding eigenvalues.

1. Eigenvectors help identify the directions (principal components) that capture the most variance in the dataset.
2. Eigenvalues indicate how much variance is captured in each of these directions.

Example of PCA

Let’s consider a dataset with hundreds of features (columns). By applying PCA, we can reduce this number to a smaller set of principal components, which represent the majority of the variance in the data.

For instance, if your dataset has 100 features, after applying PCA, you might reduce it to just 10 or 15 components. This reduction improves the computational efficiency of machine learning algorithms, as the model will now work with fewer features while still retaining most of the important information.

Here’s an example using Python:

import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

# Load example dataset
data = load_iris()
X = data.data

# Applying PCA
pca = PCA(n_components=2)  # Reduce to 2 dimensions
X_reduced = pca.fit_transform(X)

print("Reduced dataset shape:", X_reduced.shape)

In this case, the dataset originally had 4 features. PCA reduced it to 2 components while preserving most of the variance. These components are the eigenvectors, and their corresponding eigenvalues tell us how much variance each component captures.

Spectral Clustering

Another key application of eigenvectors and eigenvalues in machine learning is spectral clustering. This method involves transforming data points into a different space where clusters are more apparent.

How Spectral Clustering Works

Spectral clustering uses the eigenvectors of a similarity matrix to perform clustering. It transforms the data into a lower-dimensional space using the eigenvectors, making the structure of the clusters more obvious.

Here’s the general process:

• A similarity matrix is constructed based on pairwise distances between data points.
• The eigenvectors of this matrix are calculated.
• The top k eigenvectors are selected, and the data points are projected onto this new space (just like in PCA).
• Finally, a clustering algorithm, such as k-means, is applied to these projections.

This method is particularly useful when the clusters are not easily separable using traditional clustering methods like k-means. Spectral clustering helps by finding clusters in a transformed space, revealing hidden patterns.

Dimensionality Reduction Using Eigenvectors

Dimensionality reduction is a key application of Linear Algebra for Data Science, and eigenvectors are at the heart of this process. Reducing the number of features is essential, especially when working with large datasets where computational efficiency becomes a concern.

Why Dimensionality Reduction?

• Computational Efficiency: Fewer features mean less time required for training the model.
• Avoiding Overfitting: Reducing dimensions can also help reduce the chances of overfitting, particularly in cases where the dataset has a high number of features compared to data points.
• Improved Visualization: In some cases, reducing dimensions to 2D or 3D helps in better understanding and visualizing the data.

Eigenvectors for Dimensionality Reduction

As mentioned earlier, in methods like PCA, eigenvectors are used to identify the directions of maximum variance. By selecting only the top few eigenvectors (those associated with the largest eigenvalues), we can project the data into a lower-dimensional space.

Example: Suppose you have a dataset with 50 features, but after applying PCA, you find that 90% of the variance is captured by just 5 eigenvectors. You can now reduce the dataset from 50 to 5 dimensions without losing much information.

Practical Example

Let’s walk through a practical Python example that uses eigenvectors to reduce dimensions with PCA:

from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# Load dataset
digits = load_digits()
X = digits.data

# Apply PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# Plot the reduced dataset
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=digits.target)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA - Reduced Dimensions')
plt.show()

This example reduces a 64-feature dataset to 2 dimensions using eigenvectors from PCA, allowing us to plot and visualize the data in 2D space.

Summary of Eigenvectors and Eigenvalues in Machine Learning

Here’s a quick summary of how eigenvectors and eigenvalues are used in machine learning:

Eigenvectors and eigenvalues are not just abstract mathematical concepts—they are powerful tools in machine learning and data science. From PCA to spectral clustering, they enable us to simplify complex datasets, reduce dimensions, and find meaningful patterns.

Conclusion

In this first part of our exploration into linear algebra for data science, we’ve highlighted the foundational role it plays in manipulating data, building machine learning models, and powering real-world applications like recommendation systems and facial recognition. From understanding vectors and matrices to learning how to perform matrix operations like multiplication and transposition, linear algebra provides the mathematical backbone for transforming data and extracting insights.

Grasping these key concepts not only makes it easier to handle large datasets but also opens up pathways to implementing more complex algorithms. With tools like NumPy and TensorFlow heavily relying on linear algebra, having a solid understanding of these principles is crucial for any data scientist or machine learning practitioner.

In Part 2, we’ll delve deeper into advanced topics such as Singular Value Decomposition (SVD), tensors, and how these techniques apply to modern machine learning and AI systems. Stay tuned as we continue to explore the fascinating applications and techniques in linear algebra that help shape the future of data science.

Click Here – Part 2

FAQ

External Resources

Linear Algebra for Data Science

• Resource: Khan Academy – Linear Algebra
• Description: A comprehensive online course covering the fundamental concepts of linear algebra, including vectors, matrices, and their applications in various fields.

Understanding Vectors and Matrices in Python

• Resource: NumPy Documentation
• Description: The official NumPy documentation provides a thorough introduction to using arrays and matrices in Python, essential for data manipulation in data science.

Principal Component Analysis (PCA)

• Resource: Scikit-learn Documentation – PCA
• Description: An official guide on how to implement PCA using Scikit-learn, including examples and explanations of its use in dimensionality reduction.

About The Author

Emmimal Alexander

Welcome! I’m Emmimal Alexander, a trailblazer in the tech world with a unique background that bridges business and technology. As an Anna University Rank Holder, I hold a Master’s in Business Administration and a Bachelor’s in Computer Applications. My career began in the corporate world as an HR executive, then shifted to NSE trading, and finally led me to specialize in artificial intelligence, machine learning, deep learning, and programming languages like Python, HTML, JavaScript, and CSS.

Now, as the founder of EmitechLogic, I’m dedicated to empowering others to master the complexities of AI, ML, DL, and programming. My passion for technology and creative expression drives me to make these advanced fields accessible, practical, and engaging for learners of all levels. Through EmitechLogic, I provide insightful resources, tutorials, and discussions that help professionals and enthusiasts stay ahead in the rapidly evolving tech landscape.

Throughout my journey, I’ve worked on exciting projects like synthetic data generation, neural networks, and creative writing. My mission is to inspire curiosity, share knowledge, and foster a deeper understanding of the endless possibilities technology offers.

When I’m not writing or experimenting with new tech, you’ll find me enjoying creative projects or the beauty of nature. I invite you to explore my blog, connect through my experiences, and join me as we uncover the limitless potential of AI and innovation together!

See author's posts